2.2.2平行四边形的判定(第1课时平行四边形判定定理1,2) 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 2.2.2平行四边形的判定(第1课时平行四边形判定定理1,2) 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第2章 平行四边形
2.2.2 平行四边形的判定
第2章 平行四边形
第1课时 平行四边形的判定定理1,2
学 习 目 标
1.理解并掌握平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;(重点)
2.会运用平行四边形的判定定理判定一个四边形是平行四边形。(难点)
1. 平行四边形的定义是什么?
2. 平行四边形的性质有哪些?
知识回顾
知识讲解
动手操作
如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
四边形ABCD是平行四边形
猜想:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
B
A
D
C
一、平行四边形判定定理1
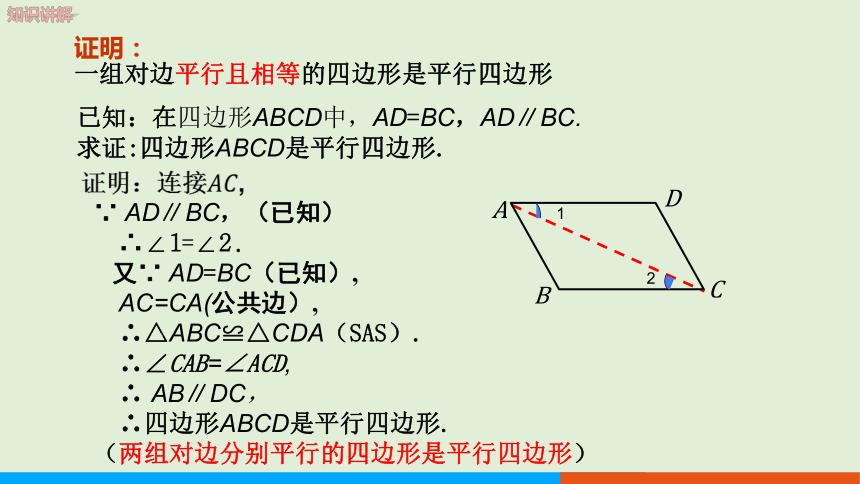
∵ AD∥BC,(已知)
∴∠1=∠2.
又∵ AD=BC(已知),
AC=CA(公共边),
∴△ABC≌△CDA(SAS).
∴∠CAB=∠ACD,
∴ AB∥DC,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
已知:在四边形ABCD中,AD=BC,AD∥BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
1
2
证明:
一组对边平行且相等的四边形是平行四边形
证明:连接,
一组对边平行且相等的四边形是平行四边形.
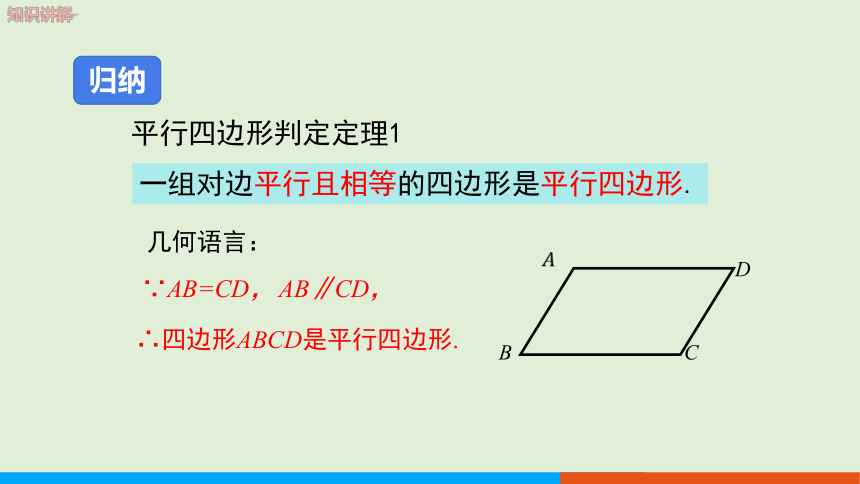
∵AB=CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
归纳
AB∥CD,
例1 如图 ,点E,F分别在平行四边形ABCD的边BC,AD上,且EC= BC,AF= AD,连接AE,CF.
求证:四边形ECFA是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴BC =AD,BC //AD.
又 ∵ EC= BC,AF= AD ,
∴EC =AF .
∵ EC //AF,∴四边形ECFA是平行四边形.
注意:
定理1中必须是同一组对边平行且相等.
思考:
一组对边平行,另一组对边相等的四边形是平行四边形吗?
两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AD=BC,AB=DC.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌△CDA,
∴∠1= ∠2, ∠3=∠4 ,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
D
A
C
1
3
2
4
B
二、平行四边形的判定定理2
几何语言:
在四边形ABCD中,
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形.
平行四边形判定定理2
两组对边分别相等的四边形是平行四边形.
C
B
D
A
归纳
例2 如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
随堂训练
1.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.
求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
2.如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.
求证:四边形DAEF是平行四边形.
解:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE.
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAEF是平行四边形.
证明:在平行四边形ABCD中,∠A=∠C(平行四边形的对边相等).
又∵AE=CG,AH=CF(已知),
∴△AEH≌△CGF(SAS),
∴EH=GF(全等三角形的对应边相等).
在平行四边形ABCD中,AB=CD,AD=BC(平行四边形的对边相等),
∴AB﹣AE=CD﹣CG,AD﹣AH=BC﹣CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH,
∴GH=EF(全等三角形的对应边相等),
∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
3.如图,已知,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.
课堂小结
平行四边形的判定
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
第2章 平行四边形
2.2.2 平行四边形的判定
第2章 平行四边形
第1课时 平行四边形的判定定理1,2
学 习 目 标
1.理解并掌握平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;(重点)
2.会运用平行四边形的判定定理判定一个四边形是平行四边形。(难点)
1. 平行四边形的定义是什么?
2. 平行四边形的性质有哪些?
知识回顾
知识讲解
动手操作
如图,将线段AB向右平移BC长度后得到线段DC,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
四边形ABCD是平行四边形
猜想:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
B
A
D
C
一、平行四边形判定定理1
∵ AD∥BC,(已知)
∴∠1=∠2.
又∵ AD=BC(已知),
AC=CA(公共边),
∴△ABC≌△CDA(SAS).
∴∠CAB=∠ACD,
∴ AB∥DC,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
已知:在四边形ABCD中,AD=BC,AD∥BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
1
2
证明:
一组对边平行且相等的四边形是平行四边形
证明:连接,
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
归纳
AB∥CD,
例1 如图 ,点E,F分别在平行四边形ABCD的边BC,AD上,且EC= BC,AF= AD,连接AE,CF.
求证:四边形ECFA是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴BC =AD,BC //AD.
又 ∵ EC= BC,AF= AD ,
∴EC =AF .
∵ EC //AF,∴四边形ECFA是平行四边形.
注意:
定理1中必须是同一组对边平行且相等.
思考:
一组对边平行,另一组对边相等的四边形是平行四边形吗?
两组对边分别相等的四边形是平行四边形.
已知:如图,在四边形ABCD中,AD=BC,AB=DC.
求证:四边形ABCD是平行四边形.
证明:连接AC,
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌△CDA,
∴∠1= ∠2, ∠3=∠4 ,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
D
A
C
1
3
2
4
B
二、平行四边形的判定定理2
几何语言:
在四边形ABCD中,
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形.
平行四边形判定定理2
两组对边分别相等的四边形是平行四边形.
C
B
D
A
归纳
例2 如图, AD⊥AC,BC⊥AC,且AB=CD,
求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形ABCD是平行四边形.
随堂训练
1.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.
求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=DB ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
2.如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.
求证:四边形DAEF是平行四边形.
解:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE.
同理可证△ABC≌△EFC,
∴AB=EF=AD,
∴四边形DAEF是平行四边形.
证明:在平行四边形ABCD中,∠A=∠C(平行四边形的对边相等).
又∵AE=CG,AH=CF(已知),
∴△AEH≌△CGF(SAS),
∴EH=GF(全等三角形的对应边相等).
在平行四边形ABCD中,AB=CD,AD=BC(平行四边形的对边相等),
∴AB﹣AE=CD﹣CG,AD﹣AH=BC﹣CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH,
∴GH=EF(全等三角形的对应边相等),
∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
3.如图,已知,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.
课堂小结
平行四边形的判定
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
