4.1 认识三角形(第3课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 4.1 认识三角形(第3课时)教学课件 北师大版中学数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览





文档简介
(共16张PPT)
第 四章 三角形
第四章 三角形
1 认识三角形
第3课时 三角形的中线和角平分线
学 习 目 标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准
确画出三角形的角平分线、中线; (重点)
2. 学会用数学知识解决实际问题的能力.(重点)
新课导入
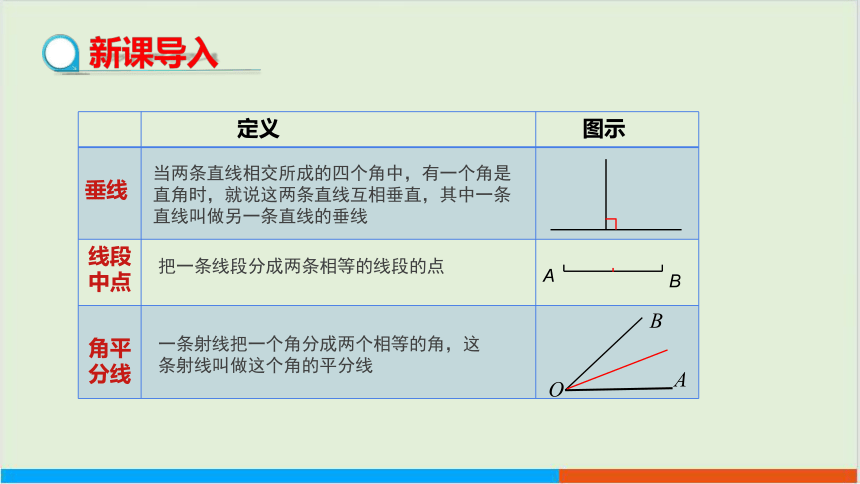
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
★ 三角形的中线
在三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线.如图,是△的边上的中线.
定义
中线
中点
想一想:由三角形的中线能得到什么结论?
(或为的中点)
知识讲解
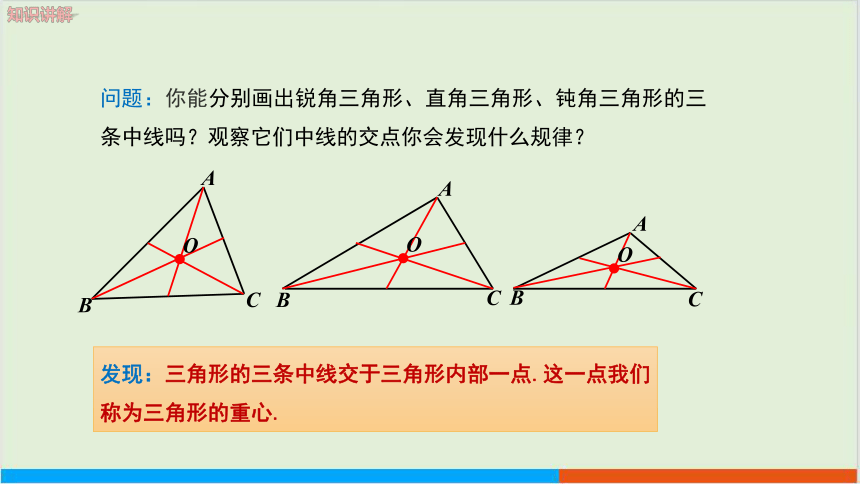
问题:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
拓展: 如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
例1 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
7cm
解析:因为△ABD的周长= AB+BD+ AD ,
△ADC的周长= AC + DC + AD ,
所以△ABD的周长△ADC的周长
=( AB+BD+ AD )( AC + DC + AD )
= ABAC=2cm.
又因为AC=5cm,
所以AB=7cm.
★ 三角形的角平分线
在三角形中,一个内角的平分线与它所对的边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.如图, 是△ 的角平分线, 或∠ =∠=∠且点在边上.
1
2
A
C
D
∠1=∠2
B
想一想:三角形的角平分线与角的角平分线相同吗
定义
不同,三角形的角平分线是线段,而角的平分线是射线
问题:请画出这个三角形的另外两条角平分线,你发现了什么?
A
B
C
D
E
F
发现:三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心.
问题:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,观察它们是否也有这样的发现?
解:因为 平分∠,∠,
所以∠.
因为∠+∠+∠,∠=50°,
所以∠ = 180°-50°-42°=88° .
因为 平分∠,
所以∠=∠.
例2 在△ 中,已知∠ = ,分别是∠,∠ 的平分线,相交于点. ∠,求∠ 的度数.
2.如图所示,在△中,分别是△,△的中线,△ 的面积是4 ,那么△ 的面积是( )
A.2.5 B.2 C.1.5 D.1
随堂训练
1.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
×
×
√
B
解:设,则.
(1)当时,有,
所以. 所以,.
(2)当,时,有,
解得,所以
所以.
因为,所以此时不能构成三角形.
综上所述,等腰三角形的腰长为8,底边长为2.
3.如图所示,在等腰三角形ABC 中,AB = AC,一腰上的中线BD 将这个等腰三角形的周长分成12和6 两部分, 求这个等腰三角形的腰长及底边长.
4.如图,AE是 △ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
课堂小结
三角形重要线段
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
第 四章 三角形
第四章 三角形
1 认识三角形
第3课时 三角形的中线和角平分线
学 习 目 标
1.了解三角形的角平分线、中线的概念并掌握其性质,会用工具准
确画出三角形的角平分线、中线; (重点)
2. 学会用数学知识解决实际问题的能力.(重点)
新课导入
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
★ 三角形的中线
在三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线.如图,是△的边上的中线.
定义
中线
中点
想一想:由三角形的中线能得到什么结论?
(或为的中点)
知识讲解
问题:你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗?观察它们中线的交点你会发现什么规律?
发现:三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
O
O
O
拓展: 如图所示,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?你能发现什么规律?
B
C
D
E
A
相等,因为两个三角形等底同高,所以它们面积相等.
发现:三角形的中线能将三角形的面积平分.
例1 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
7cm
解析:因为△ABD的周长= AB+BD+ AD ,
△ADC的周长= AC + DC + AD ,
所以△ABD的周长△ADC的周长
=( AB+BD+ AD )( AC + DC + AD )
= ABAC=2cm.
又因为AC=5cm,
所以AB=7cm.
★ 三角形的角平分线
在三角形中,一个内角的平分线与它所对的边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.如图, 是△ 的角平分线, 或∠ =∠=∠且点在边上.
1
2
A
C
D
∠1=∠2
B
想一想:三角形的角平分线与角的角平分线相同吗
定义
不同,三角形的角平分线是线段,而角的平分线是射线
问题:请画出这个三角形的另外两条角平分线,你发现了什么?
A
B
C
D
E
F
发现:三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心.
问题:分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线,观察它们是否也有这样的发现?
解:因为 平分∠,∠,
所以∠.
因为∠+∠+∠,∠=50°,
所以∠ = 180°-50°-42°=88° .
因为 平分∠,
所以∠=∠.
例2 在△ 中,已知∠ = ,分别是∠,∠ 的平分线,相交于点. ∠,求∠ 的度数.
2.如图所示,在△中,分别是△,△的中线,△ 的面积是4 ,那么△ 的面积是( )
A.2.5 B.2 C.1.5 D.1
随堂训练
1.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交 AC于E,F为AB上一点,CF交AD于H,判断下列说法的正误.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
(1)AD是△ABE的角平分线( )
(2)BE是△ABD边AD上的中线( )
(3)BE是△ABC边AC上的中线( )
×
×
√
B
解:设,则.
(1)当时,有,
所以. 所以,.
(2)当,时,有,
解得,所以
所以.
因为,所以此时不能构成三角形.
综上所述,等腰三角形的腰长为8,底边长为2.
3.如图所示,在等腰三角形ABC 中,AB = AC,一腰上的中线BD 将这个等腰三角形的周长分成12和6 两部分, 求这个等腰三角形的腰长及底边长.
4.如图,AE是 △ABC的角平分线.已知∠B=45°,∠C=60°,求∠BAE和∠AEB的度数.
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
∴∠CAE=∠BAE= ∠BAC.
课堂小结
三角形重要线段
中线
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点,这一点我们称为三角形的内心
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
