4.1 认识三角形(第4课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 4.1 认识三角形(第4课时)教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第 四章 三角形
第四章 三角形
1 认识三角形
第4课时 三角形的高
学 习 目 标
认识三角形的高,能画任意三角形的高,了解三角形三条
高所在直线交于一点;(重点)
学会用数学知识解决实际问题的能力,发展应用和自主探究
意识,培养学生的动手实践能力与合作精神.(重点)
新课导入
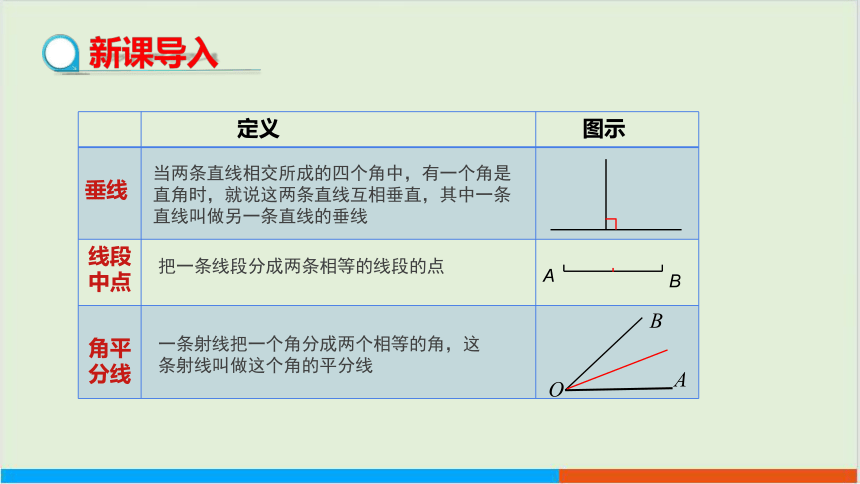
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
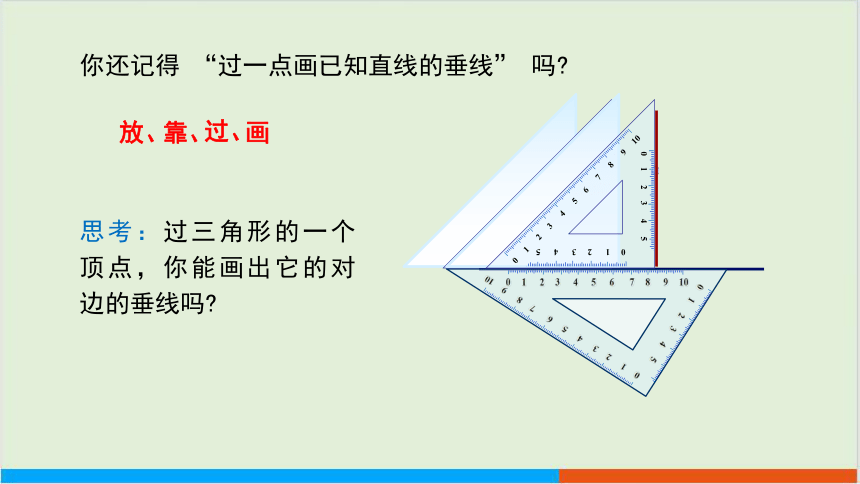
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
知识讲解
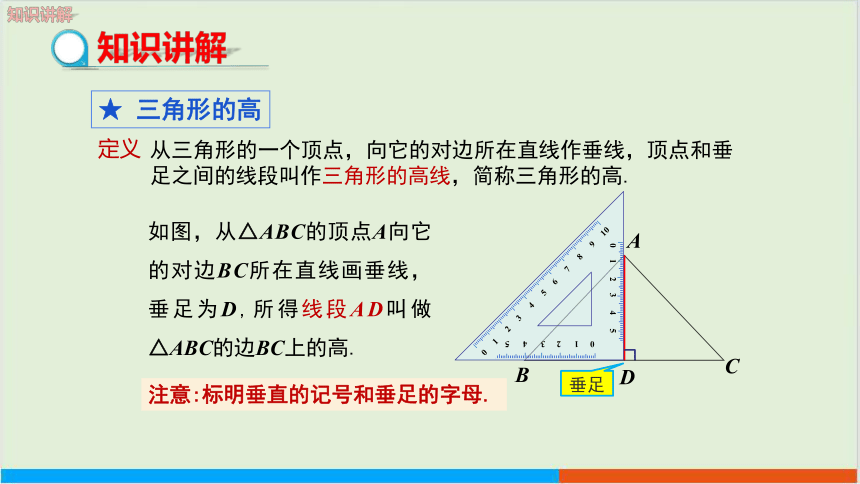
★ 三角形的高
定义
A
B
C
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
D
注意:标明垂直的记号和垂足的字母.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
垂足
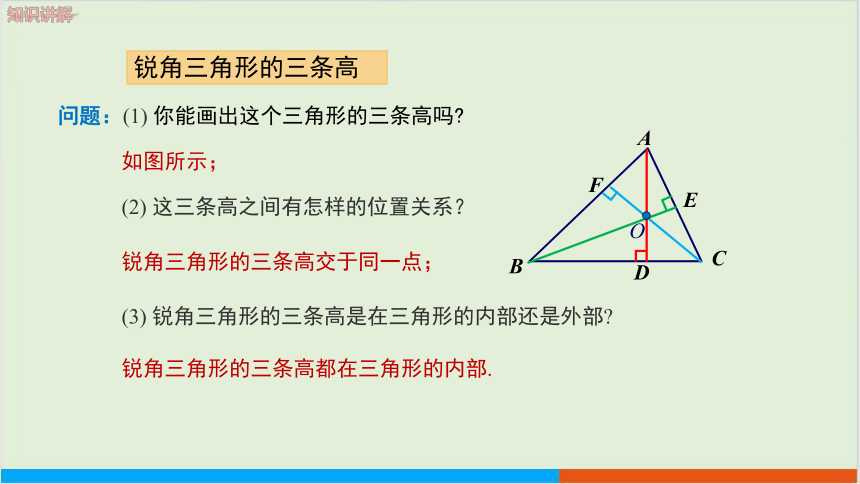
问题:(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
锐角三角形的三条高
F
E
A
B
O
C
D
直角三角形的三条高
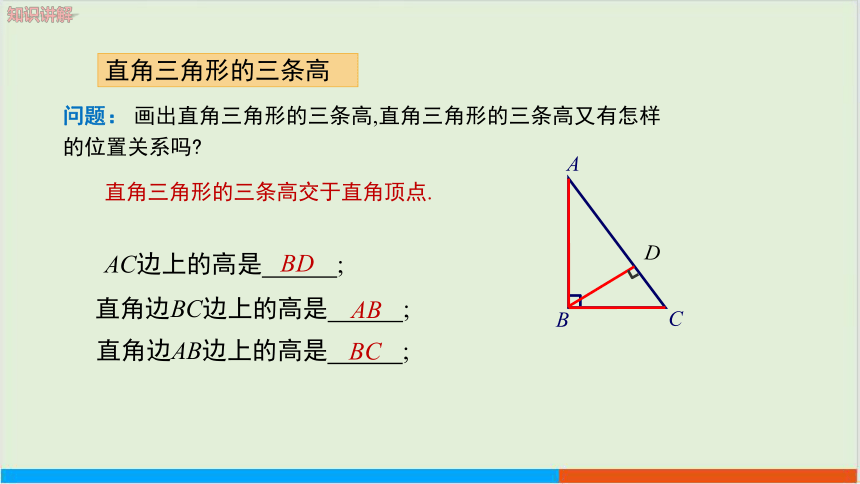
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗
A
B
C
D
直角三角形的三条高交于直角顶点.
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
AB
BC
BD
钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗
A
B
D
F
O
E
C
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
要点归纳
三角形 高及高的交点的位置 图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
例1 作△ABC的边AB上的高,下列作法中,正确的是( )
规律总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,所以
∠ADB=180°-∠B-∠BAD
=180°-30°-50°
=100°.
例3 如图所示,在△ 中,∠,∠, 是边上的高,是∠ 的平分线. 求∠ 的度数.
解:在△ 中,∵ ∠,∠,
∴ ∠ ∠∠= .
∵ 是∠的平分线,
∴ ∠ = ∠ = .
∵ 是 边上的高,∴ ∠.
在△ 中,∵ ∠ = ,∠,
∴ ∠∠∠.
∴ ∠∠ ∠.
随堂训练
1.如图,在△ABC中,EF∥AC,BD⊥AC于点D,交
EF于点G,则下列说法错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高
C.EG是△ABD的高 D.BG是△BEF的高
2.如图,CD、CE、CF分别是△ABC的高、角平分线、
中线,则下列各式中错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
C
C
3.如图所示,在△ABC中,AB=AC=5,BC=6,
AD⊥BC于点D,且AD=4,若点P在边AC上移动,
则BP的最小值为____.
4.如图,在△ABC中,AB边上的高是____ ,BC边
上 的高是____ ;在△BCF中,CF边上的高是____ .
AD
BC
CE
5.在△中,⊥于,是∠的平分线,∠,∠,求:
(1)∠的度数;
(2)∠的度数.
解:(1)∵,∴∠.
∵∠,∴∠∠;
(2)∵∠,∠,∠+∠+∠,
∴∠.
∵是∠的平分线,∴∠= ∠,
∴∠=∠+∠,∠.
课堂小结
三角形 高及高的交点的位置 图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
第 四章 三角形
第四章 三角形
1 认识三角形
第4课时 三角形的高
学 习 目 标
认识三角形的高,能画任意三角形的高,了解三角形三条
高所在直线交于一点;(重点)
学会用数学知识解决实际问题的能力,发展应用和自主探究
意识,培养学生的动手实践能力与合作精神.(重点)
新课导入
定义 图示
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
A
B
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
O
B
A
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
知识讲解
★ 三角形的高
定义
A
B
C
从三角形的一个顶点,向它的对边所在直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
D
注意:标明垂直的记号和垂足的字母.
如图,从△ABC的顶点A向它的对边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
垂足
问题:(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角形的内部还是外部
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
如图所示;
锐角三角形的三条高
F
E
A
B
O
C
D
直角三角形的三条高
问题: 画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系吗
A
B
C
D
直角三角形的三条高交于直角顶点.
直角边BC边上的高是 ;
直角边AB边上的高是 ;
AC边上的高是 ;
AB
BC
BD
钝角三角形的三条高
问题: 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系吗
A
B
D
F
O
E
C
钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点
要点归纳
三角形 高及高的交点的位置 图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
例1 作△ABC的边AB上的高,下列作法中,正确的是( )
规律总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,所以
∠ADB=180°-∠B-∠BAD
=180°-30°-50°
=100°.
例3 如图所示,在△ 中,∠,∠, 是边上的高,是∠ 的平分线. 求∠ 的度数.
解:在△ 中,∵ ∠,∠,
∴ ∠ ∠∠= .
∵ 是∠的平分线,
∴ ∠ = ∠ = .
∵ 是 边上的高,∴ ∠.
在△ 中,∵ ∠ = ,∠,
∴ ∠∠∠.
∴ ∠∠ ∠.
随堂训练
1.如图,在△ABC中,EF∥AC,BD⊥AC于点D,交
EF于点G,则下列说法错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高
C.EG是△ABD的高 D.BG是△BEF的高
2.如图,CD、CE、CF分别是△ABC的高、角平分线、
中线,则下列各式中错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
C
C
3.如图所示,在△ABC中,AB=AC=5,BC=6,
AD⊥BC于点D,且AD=4,若点P在边AC上移动,
则BP的最小值为____.
4.如图,在△ABC中,AB边上的高是____ ,BC边
上 的高是____ ;在△BCF中,CF边上的高是____ .
AD
BC
CE
5.在△中,⊥于,是∠的平分线,∠,∠,求:
(1)∠的度数;
(2)∠的度数.
解:(1)∵,∴∠.
∵∠,∴∠∠;
(2)∵∠,∠,∠+∠+∠,
∴∠.
∵是∠的平分线,∴∠= ∠,
∴∠=∠+∠,∠.
课堂小结
三角形 高及高的交点的位置 图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
