2.4 三角形的中位线 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 2.4 三角形的中位线 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
2.4 三角形的中位线
第2章 四边形
第2章 四边形
1.了解三角形中位线的概念;
2.探索并证明三角形的中位线定理;(重点)
3.会运用三角形的中位线定理进行简单的推理与计算;(难点)
学 习 目 标
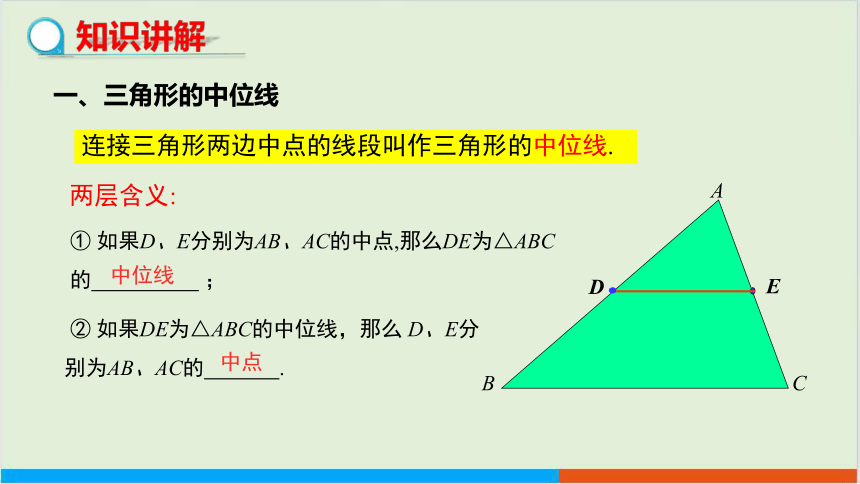
连接三角形两边中点的线段叫作三角形的中位线.
A
B
C
D
E
两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
中位线
中点
一、三角形的中位线
知识讲解
A
B
C
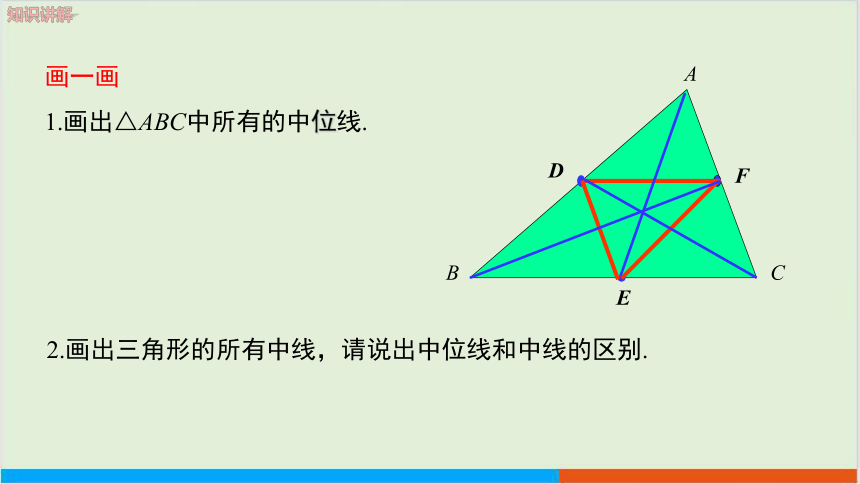
画一画
1.画出△ABC中所有的中位线.
2.画出三角形的所有中线,请说出中位线和中线的区别.
D
E
F
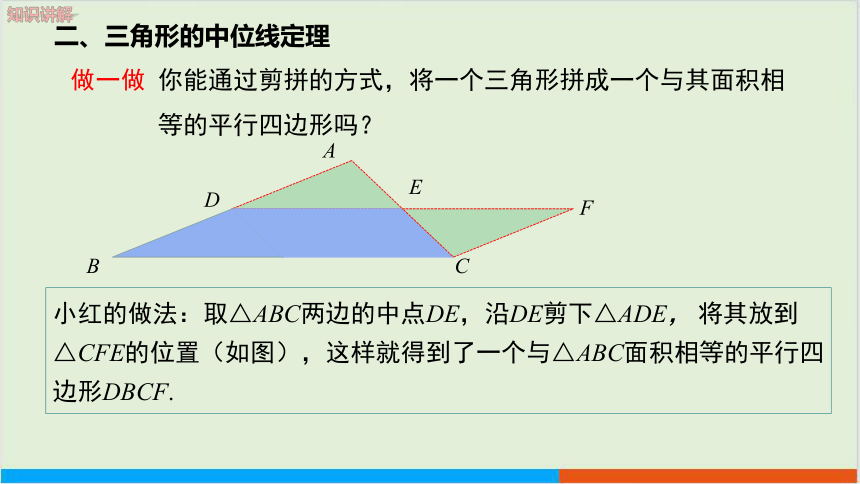
做一做 你能通过剪拼的方式,将一个三角形拼成一个与其面积相
等的平行四边形吗?
小红的做法:取△ABC两边的中点DE,沿DE剪下△ADE, 将其放到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF.
A
D
E
F
C
B
二、三角形的中位线定理
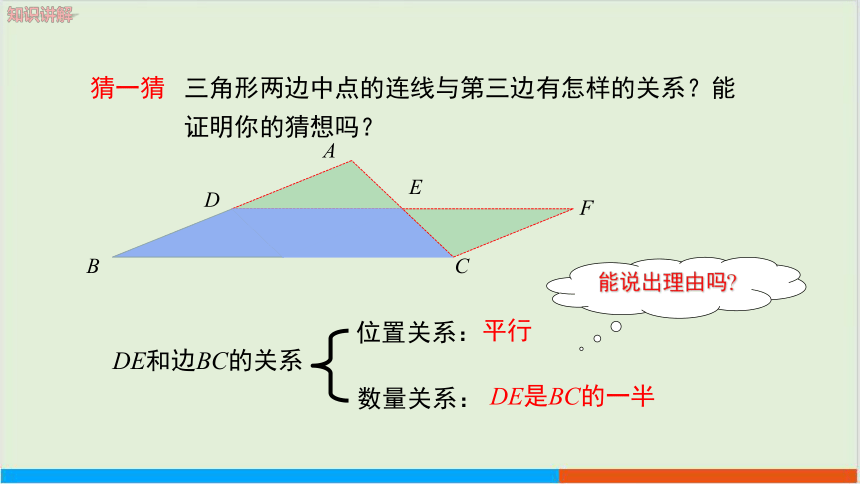
猜一猜 三角形两边中点的连线与第三边有怎样的关系?能
证明你的猜想吗?
DE和边BC的关系
数量关系:
位置关系:
平行
DE是BC的一半
能说出理由吗
A
D
E
F
C
B
测量法
已知:如图,在△ABC中,DE是△ABC的中位线. 求证:
DE∥BC,
E
A
B
C
D
F
DE= BC.
证明:如图,将△ADE绕点F旋转180°,设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E,F,,G在一条直线上.
则CF∥AD.即CF∥BD
证明法
∴四边形DBCF是平行四边形.(对边平行且相等的四边形是平行四边形)
由于旋转不改变图形的形状和大小,所以有EF=DE, CF=AD=DB, ∠F=∠ADF.
∴DF∥BC,且DF=BC
又∵EF=DE
∴
三角形中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
符号语言
D
∵DE是△ABC的中位线
总结
∴DE∥BC,
定理的两点说明
(1)从条件看,题目中若有中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理.
(2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),所以在解决相关问题时要两方面结合起来灵活应用.
在△ABC中,点D,E,F分别是AB,BC,AC的中点.
(1)图中有几个全等三角形,你是怎么知道的?你能证明吗?
(2)图中有几个平行四边形?你能证明吗?
问题探究
(3)已知:三角形的各边分别为6cm,8cm, 12cm,则连接各边中点所成三角形的周长为 ____ cm.
13
(4)已知:三角形的周长为64cm,则连接各边中点所成三角形的周长为 ____cm.
32
(5)△ABC的周长为a
D、E、F分别为△ABC各边中点,△DEF的周长为 ;
G、H、I分别为△DEF各边中点,△GHI的周长为 ;
C
A
B
D
F
E
G
H
I
像这样下去,第3个三角形的周长为 ;
第n个三角形的周长为 .
a
1
2
a
1
4
a
1
8
a
1
2n
你有什么发现?
你还有什么发现?
(6) ①如图:若D,E,F分别是△ABC三边的中点,则△DEF的面积与△ABC的面积有怎样的关系?为什么?
②已知:△ABC的面积为s,连接各边中点得△A1B1C1,再连接△A1B1C1各边中点得△A2B2C2 ……,
则第1次连接所得
△A1B1C1面积=____
第2次连接所得
△A2B2C2面积=____
第3次连接所得
△A3B3C3面积=____
第n次连接所得
△AnBnCn面积=____
S
1
4
S
1
16
S
1
64
S
1
4n
例 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
1.如左图,MN 为△ABC 的中位线,若∠ABC =61°,则∠AMN = ,若MN =12 ,则BC = .
A
M
B
C
N
61°
24
2.在△ABC中,中线CE、BF相交点O,M、N分别是OB、OC的中点,则EF和MN的关系是_______________.
平行且相等
随堂训练
3.A,B两村相隔一座大山,你能想办法测出A,B两村的直线距离AB吗?
若MN=3km,则AB=_____.
测出MN的长,就可知A、B两点的距离.
解析:在AB外选一点C,使C
能直接到达A和B,
连接AC和BC,并分别找出AC和
BC的中点M、N.
6km
思考
如果,M、N两点之间还有阻隔,你有什么解决办法?
两次利用中位线,分别取CM和CN的中点.
4.如图,在Rt△ABC 中,∠C=90°, D是斜边AB的中点,E是BC的中点.
(2)若AB=10,DE=4, 求△ABC 的面积.
(1)DE⊥BC吗?为什么?
A
B
C
D
E
∴DE∥BC,∵∠C=90°,∴DE⊥BC.
∵DE=4,∴AC=8.
∵AB=10,AC=8,∴BC=6.
∵D、E分别是AB、BC的中点,
三角形中位线
定 义
连接三角形两边中点的线段叫做三角形的中位线.
定理
三角形的中位线平行于第三边,并且等于第三边的一半.
课堂小结
2.4 三角形的中位线
第2章 四边形
第2章 四边形
1.了解三角形中位线的概念;
2.探索并证明三角形的中位线定理;(重点)
3.会运用三角形的中位线定理进行简单的推理与计算;(难点)
学 习 目 标
连接三角形两边中点的线段叫作三角形的中位线.
A
B
C
D
E
两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 .
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
中位线
中点
一、三角形的中位线
知识讲解
A
B
C
画一画
1.画出△ABC中所有的中位线.
2.画出三角形的所有中线,请说出中位线和中线的区别.
D
E
F
做一做 你能通过剪拼的方式,将一个三角形拼成一个与其面积相
等的平行四边形吗?
小红的做法:取△ABC两边的中点DE,沿DE剪下△ADE, 将其放到△CFE的位置(如图),这样就得到了一个与△ABC面积相等的平行四边形DBCF.
A
D
E
F
C
B
二、三角形的中位线定理
猜一猜 三角形两边中点的连线与第三边有怎样的关系?能
证明你的猜想吗?
DE和边BC的关系
数量关系:
位置关系:
平行
DE是BC的一半
能说出理由吗
A
D
E
F
C
B
测量法
已知:如图,在△ABC中,DE是△ABC的中位线. 求证:
DE∥BC,
E
A
B
C
D
F
DE= BC.
证明:如图,将△ADE绕点F旋转180°,设点E的像为点G,易知点A的像是点C,点F的像还是点F,且E,F,,G在一条直线上.
则CF∥AD.即CF∥BD
证明法
∴四边形DBCF是平行四边形.(对边平行且相等的四边形是平行四边形)
由于旋转不改变图形的形状和大小,所以有EF=DE, CF=AD=DB, ∠F=∠ADF.
∴DF∥BC,且DF=BC
又∵EF=DE
∴
三角形中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
符号语言
D
∵DE是△ABC的中位线
总结
∴DE∥BC,
定理的两点说明
(1)从条件看,题目中若有中点,尤其是两个或者两个以上的中点时我们就要联想到三角形的中位线定理.
(2)从结论看,它既可以得到线段的位置关系(平行),又可以得到线段的数量关系(倍分关系),所以在解决相关问题时要两方面结合起来灵活应用.
在△ABC中,点D,E,F分别是AB,BC,AC的中点.
(1)图中有几个全等三角形,你是怎么知道的?你能证明吗?
(2)图中有几个平行四边形?你能证明吗?
问题探究
(3)已知:三角形的各边分别为6cm,8cm, 12cm,则连接各边中点所成三角形的周长为 ____ cm.
13
(4)已知:三角形的周长为64cm,则连接各边中点所成三角形的周长为 ____cm.
32
(5)△ABC的周长为a
D、E、F分别为△ABC各边中点,△DEF的周长为 ;
G、H、I分别为△DEF各边中点,△GHI的周长为 ;
C
A
B
D
F
E
G
H
I
像这样下去,第3个三角形的周长为 ;
第n个三角形的周长为 .
a
1
2
a
1
4
a
1
8
a
1
2n
你有什么发现?
你还有什么发现?
(6) ①如图:若D,E,F分别是△ABC三边的中点,则△DEF的面积与△ABC的面积有怎样的关系?为什么?
②已知:△ABC的面积为s,连接各边中点得△A1B1C1,再连接△A1B1C1各边中点得△A2B2C2 ……,
则第1次连接所得
△A1B1C1面积=____
第2次连接所得
△A2B2C2面积=____
第3次连接所得
△A3B3C3面积=____
第n次连接所得
△AnBnCn面积=____
S
1
4
S
1
16
S
1
64
S
1
4n
例 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
求证:四边形EFGH是平行四边形.
分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
1.如左图,MN 为△ABC 的中位线,若∠ABC =61°,则∠AMN = ,若MN =12 ,则BC = .
A
M
B
C
N
61°
24
2.在△ABC中,中线CE、BF相交点O,M、N分别是OB、OC的中点,则EF和MN的关系是_______________.
平行且相等
随堂训练
3.A,B两村相隔一座大山,你能想办法测出A,B两村的直线距离AB吗?
若MN=3km,则AB=_____.
测出MN的长,就可知A、B两点的距离.
解析:在AB外选一点C,使C
能直接到达A和B,
连接AC和BC,并分别找出AC和
BC的中点M、N.
6km
思考
如果,M、N两点之间还有阻隔,你有什么解决办法?
两次利用中位线,分别取CM和CN的中点.
4.如图,在Rt△ABC 中,∠C=90°, D是斜边AB的中点,E是BC的中点.
(2)若AB=10,DE=4, 求△ABC 的面积.
(1)DE⊥BC吗?为什么?
A
B
C
D
E
∴DE∥BC,∵∠C=90°,∴DE⊥BC.
∵DE=4,∴AC=8.
∵AB=10,AC=8,∴BC=6.
∵D、E分别是AB、BC的中点,
三角形中位线
定 义
连接三角形两边中点的线段叫做三角形的中位线.
定理
三角形的中位线平行于第三边,并且等于第三边的一半.
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
