3.1图形的平移(第2课时)教学详案--北师大版初中数学八年级(下)
文档属性
| 名称 | 3.1图形的平移(第2课时)教学详案--北师大版初中数学八年级(下) |  | |
| 格式 | docx | ||
| 文件大小 | 619.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:11 | ||
图片预览


文档简介
3.1 图形的平移(第2课时 平面直角坐标系中沿x轴或y轴的一次平移)
教学目标
1.能由坐标系中图形的位置变化说出对应点的坐标之间的变化情况(一次变化).
2.能由对应点坐标之间的变化说出坐标系中图形的位置变化情况(一次变化).
3.掌握图形平移在平面直角坐标系中的坐标变化规律,认识图形变换与坐标之间的内在联系.
教学重点难点
重点: 理解和掌握图形平移在直角坐标系中的坐标变化规律.
难点:对图形平移在平面直角坐标系中的坐标变化规律的探究.
教学过程
导入新课
图中的“鱼”是将坐标为:(0,0), (5,4) ,(3,0) ,(5,1), (5,-1) ,(3,0), (4,-2), (0,0)的点用线段依次连接而成的.
【思考】
你能画出将这条“鱼”向右平移5个单位长度的图形吗?你能发现平移前后图形对应点的坐标之间有什么关系吗?
探究新知
一、预习新知
阅读教材P68~P69的内容,回答下列问题.
在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变,可简记为左、右平移,横变纵不变,“右加左减”.反过来也是成立的.
2.在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变,可简记为上、下平移,纵变横不变,“上加下减”.反过来也是成立的.
二、合作探究
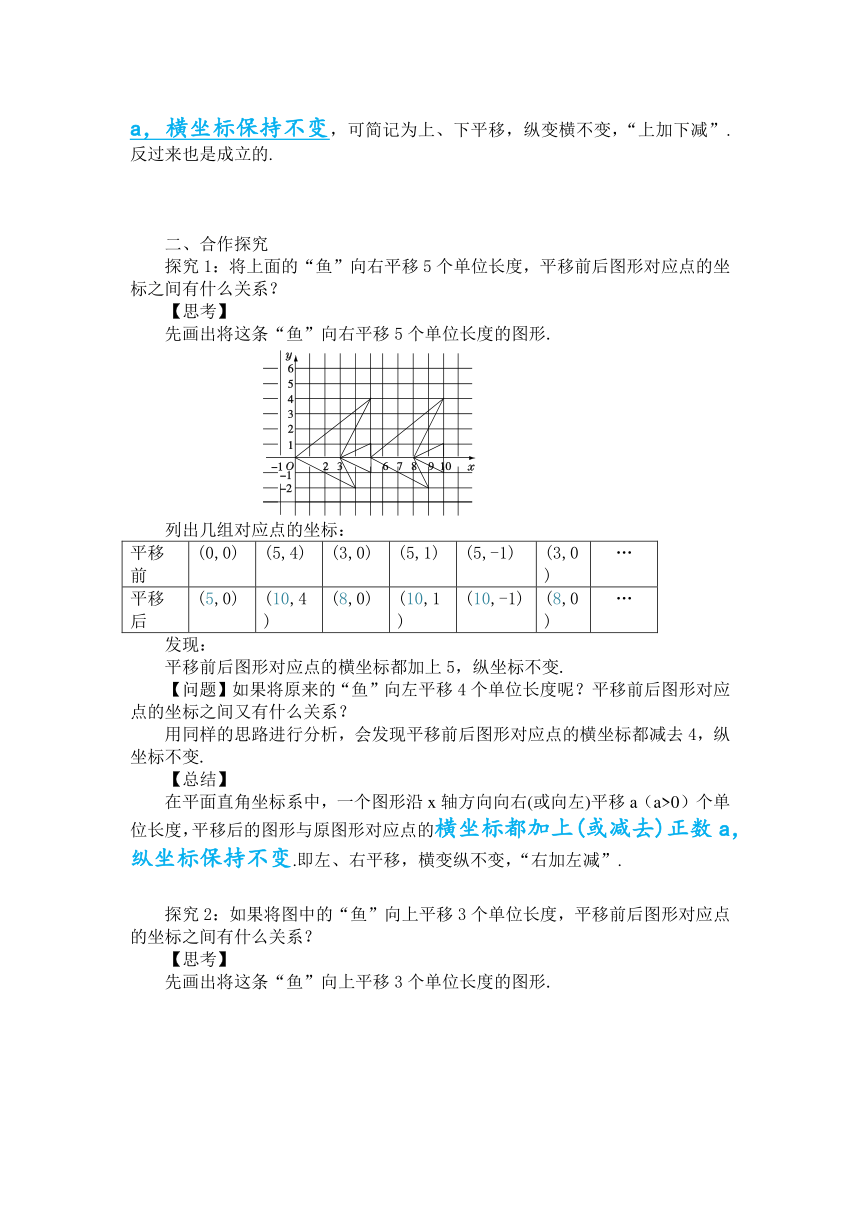
探究1:将上面的“鱼”向右平移5个单位长度,平移前后图形对应点的坐标之间有什么关系?
【思考】
先画出将这条“鱼”向右平移5个单位长度的图形.
列出几组对应点的坐标:
平移前 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
平移后 (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) …
发现:
平移前后图形对应点的横坐标都加上5,纵坐标不变.
【问题】如果将原来的“鱼”向左平移4个单位长度呢?平移前后图形对应点的坐标之间又有什么关系?
用同样的思路进行分析,会发现平移前后图形对应点的横坐标都减去4,纵坐标不变.
【总结】
在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变.即左、右平移,横变纵不变,“右加左减”.
探究2:如果将图中的“鱼”向上平移3个单位长度,平移前后图形对应点的坐标之间有什么关系?
【思考】
先画出将这条“鱼”向上平移3个单位长度的图形.
列出几组对应点的坐标:
平移前 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
平移后 (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) …
发现:
平移前后图形对应点的纵坐标都加上3,横坐标不变.
【问题】如果将原来的“鱼”向下平移2个单位长度呢?平移前后图形对应点的坐标之间又有什么关系?
用同样的思路进行分析,会发现平移前后图形对应点的纵坐标都减去2,横坐标不变.
【总结】
在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变.即上、下平移,纵变横不变,“上加下减”.
探究3:将图中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加5,再将得到的点用线段依次连接起来,从而画出一条“新鱼”,这条“新鱼”与原来的“鱼”相比,有什么变化?
【思考】
先列出新的顶点的坐标,再画出这条“新鱼”.
原顶点 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
新顶点 (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) …
发现:
这条“新鱼”是由原来的“鱼”沿x轴向右平移5个单位长度得到的.
【问题】
如果是纵坐标保持不变,横坐标分别减2呢?画出的“新鱼”与原来的“鱼”相比,有什么变化?
用同样的方法进行分析,会发现这条“新鱼”是由原来的“鱼”沿x轴向左平移2个单位长度得到的.
【总结】
在平面直角坐标系中,如果把图形中所有点的横坐标都加上(或减去)一个正数a,纵坐标保持不变,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
探究4:如果将图中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加3,所得到的“新鱼”与原来的“鱼”相比,有什么变化?
【思考】
先列出新的顶点的坐标,再画出这条“新鱼”.
原顶点 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
新顶点 (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) …
发现:
这条“新鱼”是由原来的“鱼”沿y轴向上平移3个单位长度得到的.
【问题】
如果是横坐标保持不变,纵坐标分别减2呢?画出的“新鱼”与原来的“鱼”相比,有什么变化?
同样的方法进行分析,会发现这条“新鱼”是由原来的“鱼”沿y轴向下平移2个单位长度得到的.
【总结】
在平面直角坐标系中,如果把图形中所有点的纵坐标都加上(或减去)一个正数a,横坐标保持不变,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
课堂练习
1.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点的坐标变化为( )
A.横坐标不变,纵坐标减少3个单位长度
B.纵坐标不变,横坐标减少3个单位长度
C.横、纵坐标都没有变化
D.横、纵坐标都减少3个单位长度
2.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(4,5)、B(1,2)、C(4,2),将△ABC向左平移5个单位长度后,点A的对应点A′的坐标是( )
A.(0,5) B.(-1,5)
C.(9,5) D.(-1,0)
3.如图所示,在直角坐标系中,点A的坐标为(-1,2),点C的坐标为(-3,0),将线段AC沿x轴向右平移3个单位长度,此时点A的对应点的坐标为 .
4.如图所示,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去5,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1,所得△A1B1C1与△ABC的大小、形状和位置上有什么关系?
(2)将△ABC三个顶点的纵坐标都减去4,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
参考答案
1.B 2.B 3.(2,2)
4.解:(1)根据题意,得点A1(-1,3)、B1(-2,1)、C1(-4,2),所得△A1B1C1与△ABC的大小、形状完全一样,只是把△ABC向左平移了5个单位长度.
(2)根据题意,得点A2(4,-1)、B2(3,-3)、C2(1,-2),所得△A2B2C2与△ABC的大小、形状完全一样,只是把△ABC向下平移了4个单位长度.
课堂小结
平移方向 平移距离 对应点的坐标
沿x轴 方向 向右平移 a个单位长 度(a>0) (x+a,y)
向左平移 (x-a,y)
沿y轴 方向 向上平移 (x,y+a)
向下平移 (x,y-a)
布置作业
完成教材习题3.2
板书设计
图形的平移
1.在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变.即左、右平移,横变纵不变,“右加左减”.
2.在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变.即上、下平移,纵变横不变,“上加下减”.
3.在平面直角坐标系中,如果把图形中所有点的横坐标都加上(或减去)一个正数a,纵坐标保持不变,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
4.在平面直角坐标系中,如果把图形中所有点的纵坐标都加上(或减去)一个正数a,横坐标保持不变,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
教学目标
1.能由坐标系中图形的位置变化说出对应点的坐标之间的变化情况(一次变化).
2.能由对应点坐标之间的变化说出坐标系中图形的位置变化情况(一次变化).
3.掌握图形平移在平面直角坐标系中的坐标变化规律,认识图形变换与坐标之间的内在联系.
教学重点难点
重点: 理解和掌握图形平移在直角坐标系中的坐标变化规律.
难点:对图形平移在平面直角坐标系中的坐标变化规律的探究.
教学过程
导入新课
图中的“鱼”是将坐标为:(0,0), (5,4) ,(3,0) ,(5,1), (5,-1) ,(3,0), (4,-2), (0,0)的点用线段依次连接而成的.
【思考】
你能画出将这条“鱼”向右平移5个单位长度的图形吗?你能发现平移前后图形对应点的坐标之间有什么关系吗?
探究新知
一、预习新知
阅读教材P68~P69的内容,回答下列问题.
在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变,可简记为左、右平移,横变纵不变,“右加左减”.反过来也是成立的.
2.在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变,可简记为上、下平移,纵变横不变,“上加下减”.反过来也是成立的.
二、合作探究
探究1:将上面的“鱼”向右平移5个单位长度,平移前后图形对应点的坐标之间有什么关系?
【思考】
先画出将这条“鱼”向右平移5个单位长度的图形.
列出几组对应点的坐标:
平移前 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
平移后 (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) …
发现:
平移前后图形对应点的横坐标都加上5,纵坐标不变.
【问题】如果将原来的“鱼”向左平移4个单位长度呢?平移前后图形对应点的坐标之间又有什么关系?
用同样的思路进行分析,会发现平移前后图形对应点的横坐标都减去4,纵坐标不变.
【总结】
在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变.即左、右平移,横变纵不变,“右加左减”.
探究2:如果将图中的“鱼”向上平移3个单位长度,平移前后图形对应点的坐标之间有什么关系?
【思考】
先画出将这条“鱼”向上平移3个单位长度的图形.
列出几组对应点的坐标:
平移前 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
平移后 (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) …
发现:
平移前后图形对应点的纵坐标都加上3,横坐标不变.
【问题】如果将原来的“鱼”向下平移2个单位长度呢?平移前后图形对应点的坐标之间又有什么关系?
用同样的思路进行分析,会发现平移前后图形对应点的纵坐标都减去2,横坐标不变.
【总结】
在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变.即上、下平移,纵变横不变,“上加下减”.
探究3:将图中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加5,再将得到的点用线段依次连接起来,从而画出一条“新鱼”,这条“新鱼”与原来的“鱼”相比,有什么变化?
【思考】
先列出新的顶点的坐标,再画出这条“新鱼”.
原顶点 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
新顶点 (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) …
发现:
这条“新鱼”是由原来的“鱼”沿x轴向右平移5个单位长度得到的.
【问题】
如果是纵坐标保持不变,横坐标分别减2呢?画出的“新鱼”与原来的“鱼”相比,有什么变化?
用同样的方法进行分析,会发现这条“新鱼”是由原来的“鱼”沿x轴向左平移2个单位长度得到的.
【总结】
在平面直角坐标系中,如果把图形中所有点的横坐标都加上(或减去)一个正数a,纵坐标保持不变,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
探究4:如果将图中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加3,所得到的“新鱼”与原来的“鱼”相比,有什么变化?
【思考】
先列出新的顶点的坐标,再画出这条“新鱼”.
原顶点 (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) …
新顶点 (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) …
发现:
这条“新鱼”是由原来的“鱼”沿y轴向上平移3个单位长度得到的.
【问题】
如果是横坐标保持不变,纵坐标分别减2呢?画出的“新鱼”与原来的“鱼”相比,有什么变化?
同样的方法进行分析,会发现这条“新鱼”是由原来的“鱼”沿y轴向下平移2个单位长度得到的.
【总结】
在平面直角坐标系中,如果把图形中所有点的纵坐标都加上(或减去)一个正数a,横坐标保持不变,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
课堂练习
1.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点的坐标变化为( )
A.横坐标不变,纵坐标减少3个单位长度
B.纵坐标不变,横坐标减少3个单位长度
C.横、纵坐标都没有变化
D.横、纵坐标都减少3个单位长度
2.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(4,5)、B(1,2)、C(4,2),将△ABC向左平移5个单位长度后,点A的对应点A′的坐标是( )
A.(0,5) B.(-1,5)
C.(9,5) D.(-1,0)
3.如图所示,在直角坐标系中,点A的坐标为(-1,2),点C的坐标为(-3,0),将线段AC沿x轴向右平移3个单位长度,此时点A的对应点的坐标为 .
4.如图所示,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去5,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1,所得△A1B1C1与△ABC的大小、形状和位置上有什么关系?
(2)将△ABC三个顶点的纵坐标都减去4,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2,所得△A2B2C2与△ABC的大小、形状和位置上有什么关系?
参考答案
1.B 2.B 3.(2,2)
4.解:(1)根据题意,得点A1(-1,3)、B1(-2,1)、C1(-4,2),所得△A1B1C1与△ABC的大小、形状完全一样,只是把△ABC向左平移了5个单位长度.
(2)根据题意,得点A2(4,-1)、B2(3,-3)、C2(1,-2),所得△A2B2C2与△ABC的大小、形状完全一样,只是把△ABC向下平移了4个单位长度.
课堂小结
平移方向 平移距离 对应点的坐标
沿x轴 方向 向右平移 a个单位长 度(a>0) (x+a,y)
向左平移 (x-a,y)
沿y轴 方向 向上平移 (x,y+a)
向下平移 (x,y-a)
布置作业
完成教材习题3.2
板书设计
图形的平移
1.在平面直角坐标系中,一个图形沿x轴方向向右(或向左)平移a(a>0)个单位长度,平移后的图形与原图形对应点的横坐标都加上(或减去)正数a,纵坐标保持不变.即左、右平移,横变纵不变,“右加左减”.
2.在平面直角坐标系中,一个图形沿y轴方向向上(或向下)平移a(a>0)个单位长度,平移后的图形与原图形对应点的纵坐标都加上(或减去)正数a,横坐标保持不变.即上、下平移,纵变横不变,“上加下减”.
3.在平面直角坐标系中,如果把图形中所有点的横坐标都加上(或减去)一个正数a,纵坐标保持不变,相应的新图形就是把原来的图形沿着x轴向右(或向左)平移a个单位长度.
4.在平面直角坐标系中,如果把图形中所有点的纵坐标都加上(或减去)一个正数a,横坐标保持不变,相应的新图形就是把原来的图形沿着y轴向上(或向下)平移a个单位长度.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
