3.1平面直角坐标系(第1课时 平面直角坐标系) 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 3.1平面直角坐标系(第1课时 平面直角坐标系) 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
第3章 图形与坐标
3.1 平面直角坐标系
第3章 图形与坐标
第1课时 平面直角坐标系
学 习 目 标
1
2
了解平面直角坐标系及相关概念.
知道平面直角坐标系内点与坐标是一一对应的.(难点)
3
用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.(重点)
新课导入
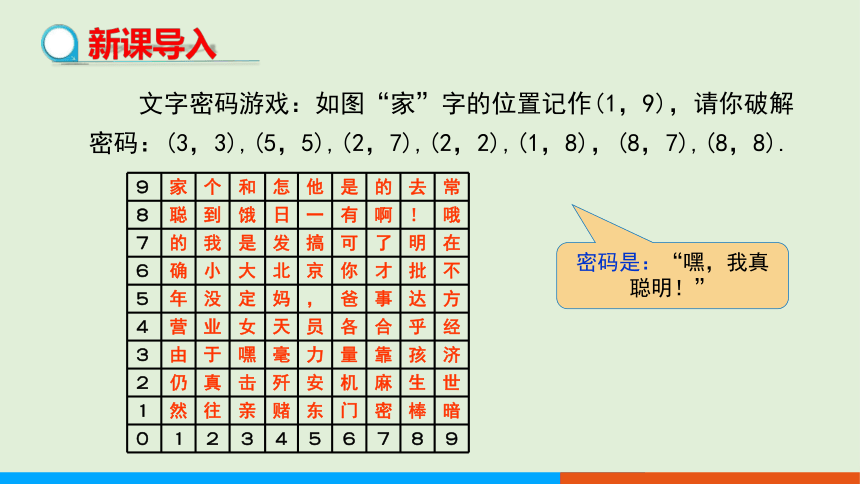
文字密码游戏:如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8).
9 家 个 和 怎 他 是 的 去 常
8 聪 到 饿 日 一 有 啊 ! 哦
7 的 我 是 发 搞 可 了 明 在
6 确 小 大 北 京 你 才 批 不
5 年 没 定 妈 , 爸 事 达 方
4 营 业 女 天 员 各 合 乎 经
3 由 于 嘿 毫 力 量 靠 孩 济
2 仍 真 击 歼 安 机 麻 生 世
1 然 往 亲 赌 东 门 密 棒 暗
0 1 2 3 4 5 6 7 8 9
密码是:“嘿,我真聪明!”
(2,2)
小明
王健
1
2
3
4
5
行
1
2
3
4
5
列
(1,3)
(5,5)
(4,5)
(5,2)
(5,4)
知识讲解
用数对表示位置
问题1: 如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,3),(2,2),(5,5),(4,5),(5,2),(5,4).
问题2: 由上面可知,“第1列第3行”简记为(1,3)(约定列在前,行在后),那么“第3列第5行”能简记成什么?(6,7)表示的含义是什么?
“第3列第5行” 记为(3,5);(6,7)表示的含义是第6列第7行.
平面直角坐标系
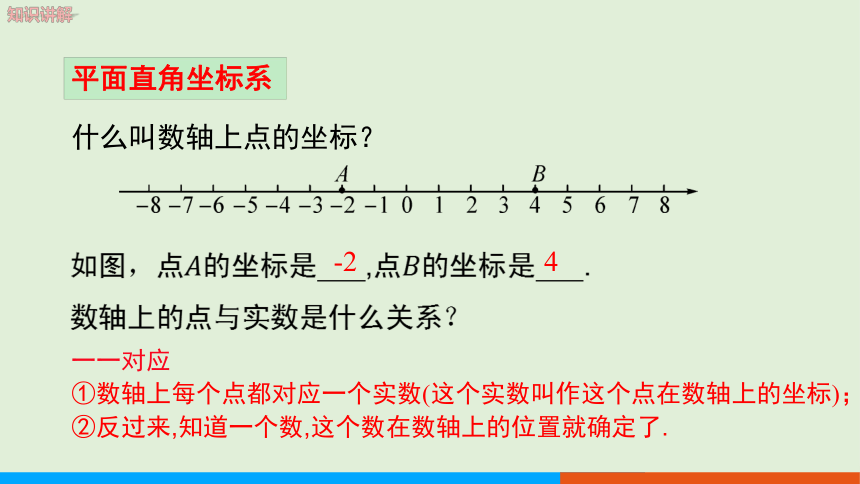
什么叫数轴上点的坐标?
如图,点的坐标是 ,点的坐标是 .
数轴上的点与实数是什么关系?
-2
4
一一对应
①数轴上每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
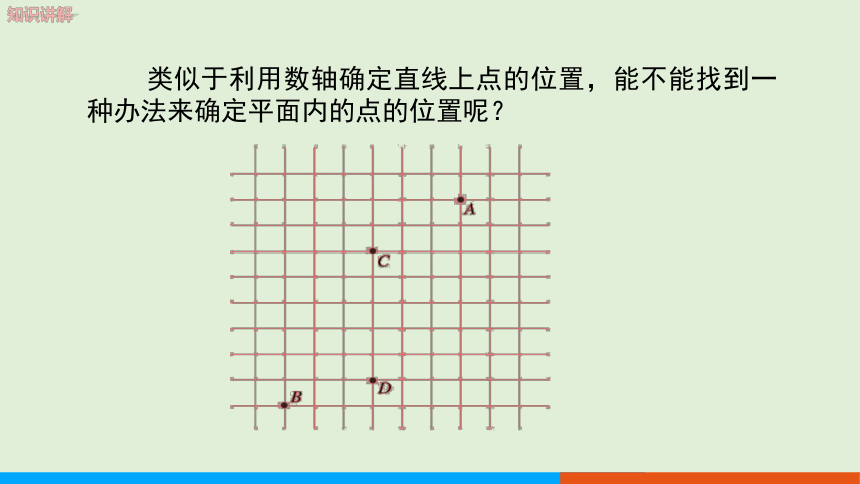
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
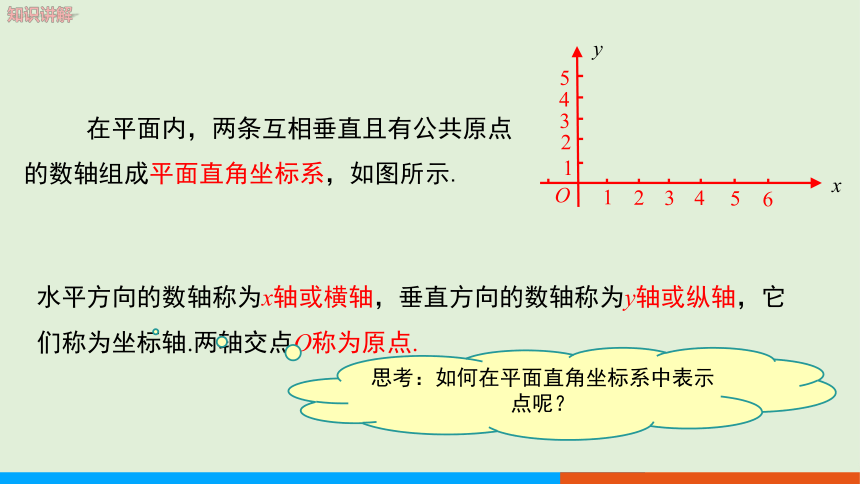
水平方向的数轴称为x轴或横轴,垂直方向的数轴称为y轴或纵轴,它们称为坐标轴.两轴交点O称为原点.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,如图所示.
y
O
x
1
2
3
4
5
1
2
3
4
5
6
思考:如何在平面直角坐标系中表示点呢?
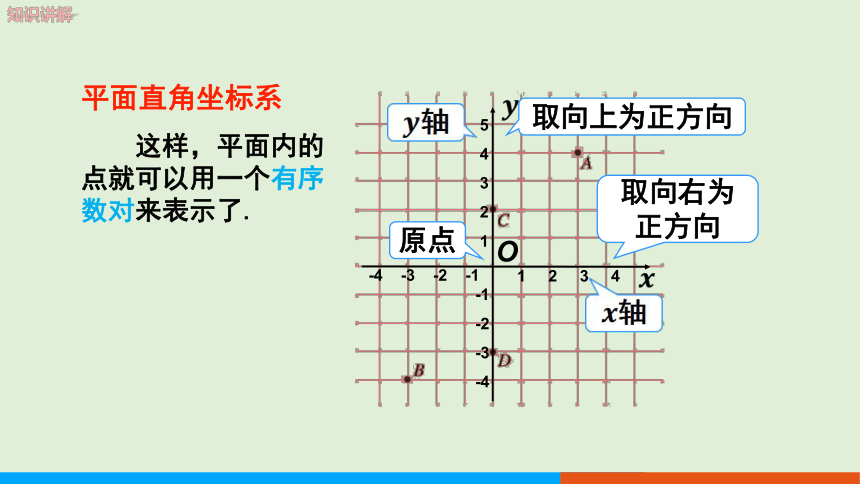
这样,平面内的点就可以用一个有序数对来表示了.
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
轴
轴
原点
平面直角坐标系
取向右为正方向
取向上为正方向
总结:平面直角坐标系中两坐标轴的特征:
①互相垂直;
②原点重合;
③通常取向上、向右为正方向;
④单位长度一般取相同的,在有些实际问题中,两坐标轴上的单位长度可以不同.
点的坐标
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3).
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
再由P点向y轴画垂线,垂足N在y轴上的坐标是3,称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是是-2,称为点的横坐标.
P
N
M
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
原点的坐标是?
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
( , )
0
0
( , )
0
2
( , )
0
-3
.
( , )
-4
0
.
( , )
2
0
.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
思考:在平面直角坐标系中找点A(-2,-3).
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴
的垂线;
(3)垂线的交点就是该坐标对应的点.
A
总结:
A
B
C
E
F
D
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
例1
直角坐标系中点的坐标的特征
坐标平面被两条坐标轴分成 个部分.
四
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
每个部分称为象限.
第一象限
第二象限
第四象限
第三象限
坐标轴上的点不属于任何象限!
交流:不看平面直角坐标系,你能迅速说出 (4,5) , (-2,3), (-4, -1), (2.5,-2), (-5,0),(0,-5),(3,0), (0,3),(0,0)所在的象限吗?你的方法又是什么?
活动: 观察坐标系,找出下列各点所处象限及点的坐标的特征.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
坐标轴上的点的坐标有什么特征呢?
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴 y轴 +
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
思考:坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例2
例3 点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
【方法总结】坐标轴上的点的坐标特点:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值,进而求出点的坐标.
随堂训练
1.写出图中点的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
L
.
M
.
N
.
P
.
Q
.
R
.
2.在图中描出下列各点:(-5,-3), M(4,0), N(-6,2), P(5,-3.5), Q(0,5), R(6,2).
4.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
5.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点
的坐标为 .
3
(5,-4)
-1
3.已知a那么点P(a,-b)在第 象限.
二
6.在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点()的坐标满足;
(2)点的坐标满足;
(3)点的坐标满足;
(4)点的坐标满足.
第一、三象限
第二、四象限
在任意一条坐标轴上
在原点处
课堂小结
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
第3章 图形与坐标
3.1 平面直角坐标系
第3章 图形与坐标
第1课时 平面直角坐标系
学 习 目 标
1
2
了解平面直角坐标系及相关概念.
知道平面直角坐标系内点与坐标是一一对应的.(难点)
3
用象限或坐标轴说明直角坐标系内点的位置,能根据横、纵坐标的符号确定点的位置.(重点)
新课导入
文字密码游戏:如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8).
9 家 个 和 怎 他 是 的 去 常
8 聪 到 饿 日 一 有 啊 ! 哦
7 的 我 是 发 搞 可 了 明 在
6 确 小 大 北 京 你 才 批 不
5 年 没 定 妈 , 爸 事 达 方
4 营 业 女 天 员 各 合 乎 经
3 由 于 嘿 毫 力 量 靠 孩 济
2 仍 真 击 歼 安 机 麻 生 世
1 然 往 亲 赌 东 门 密 棒 暗
0 1 2 3 4 5 6 7 8 9
密码是:“嘿,我真聪明!”
(2,2)
小明
王健
1
2
3
4
5
行
1
2
3
4
5
列
(1,3)
(5,5)
(4,5)
(5,2)
(5,4)
知识讲解
用数对表示位置
问题1: 如图是一个教室平面图,你能根据以下座位找到对应的同学参加数学问题讨论吗?
(1,3),(2,2),(5,5),(4,5),(5,2),(5,4).
问题2: 由上面可知,“第1列第3行”简记为(1,3)(约定列在前,行在后),那么“第3列第5行”能简记成什么?(6,7)表示的含义是什么?
“第3列第5行” 记为(3,5);(6,7)表示的含义是第6列第7行.
平面直角坐标系
什么叫数轴上点的坐标?
如图,点的坐标是 ,点的坐标是 .
数轴上的点与实数是什么关系?
-2
4
一一对应
①数轴上每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
水平方向的数轴称为x轴或横轴,垂直方向的数轴称为y轴或纵轴,它们称为坐标轴.两轴交点O称为原点.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系,如图所示.
y
O
x
1
2
3
4
5
1
2
3
4
5
6
思考:如何在平面直角坐标系中表示点呢?
这样,平面内的点就可以用一个有序数对来表示了.
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
轴
轴
原点
平面直角坐标系
取向右为正方向
取向上为正方向
总结:平面直角坐标系中两坐标轴的特征:
①互相垂直;
②原点重合;
③通常取向上、向右为正方向;
④单位长度一般取相同的,在有些实际问题中,两坐标轴上的单位长度可以不同.
点的坐标
这样P点的横坐标是-2,纵坐标是3,规定把横坐标写在前,纵坐标在后,记作:P(-2,3).
P(-2,3)就叫做点P在平面直角坐标系中的坐标,简称点P的坐标.
-4 -3 -2 -1 0 1 2 3
1
2
3
4
-1
-2
-3
-4
x
y
思考:如图点P如何表示呢?
再由P点向y轴画垂线,垂足N在y轴上的坐标是3,称为P点的纵坐标.
先由P点向x轴画垂线,垂足M在x轴上的坐标是是-2,称为点的横坐标.
P
N
M
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
原点的坐标是?
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
( , )
0
0
( , )
0
2
( , )
0
-3
.
( , )
-4
0
.
( , )
2
0
.
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
思考:在平面直角坐标系中找点A(-2,-3).
由坐标找点的方法:
(1)先找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴
的垂线;
(3)垂线的交点就是该坐标对应的点.
A
总结:
A
B
C
E
F
D
写出下图中的多边形ABCDEF各个顶点的坐标.
1
2
3
4
-1
-2
1
2
3
-1
-2
-3
【答案】
A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
y
O
x
例1
直角坐标系中点的坐标的特征
坐标平面被两条坐标轴分成 个部分.
四
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
每个部分称为象限.
第一象限
第二象限
第四象限
第三象限
坐标轴上的点不属于任何象限!
交流:不看平面直角坐标系,你能迅速说出 (4,5) , (-2,3), (-4, -1), (2.5,-2), (-5,0),(0,-5),(3,0), (0,3),(0,0)所在的象限吗?你的方法又是什么?
活动: 观察坐标系,找出下列各点所处象限及点的坐标的特征.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
坐标轴上的点的坐标有什么特征呢?
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴 y轴 +
+
-
+
-
-
+
-
纵坐标为0
横坐标为0
思考:坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例2
例3 点A(m+3,m+1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
【解析】点A(m+3,m+1)在x轴上,根据x轴上点的坐标特征知m+1=0,求出m的值代入m+3中即可.
B
【方法总结】坐标轴上的点的坐标特点:x轴上的点的纵坐标为0,y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值,进而求出点的坐标.
随堂训练
1.写出图中点的坐标.
(-2,-2)
(-5,4)
(5,-4)
(2,5)
(-3,0)
(0,-3)
L
.
M
.
N
.
P
.
Q
.
R
.
2.在图中描出下列各点:(-5,-3), M(4,0), N(-6,2), P(5,-3.5), Q(0,5), R(6,2).
4.已知P点坐标为(a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
5.若点P(x,y)在第四象限,|x|=5,|y|=4,则P点
的坐标为 .
3
(5,-4)
-1
3.已知a
二
6.在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限或哪条坐标轴上:
(1)点()的坐标满足;
(2)点的坐标满足;
(3)点的坐标满足;
(4)点的坐标满足.
第一、三象限
第二、四象限
在任意一条坐标轴上
在原点处
课堂小结
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
