4.5 利用三角形全等测距离教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 4.5 利用三角形全等测距离教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览







文档简介
(共22张PPT)
第 四章 三角形
第四章 三角形
5 利用三角形全等测距离
学 习 目 标
1.复习并归纳三角形全等的判定及性质;
2.能够根据三角形全等测定两点间的距离,并解
决实际问题.(重点,难点)
复习导入
1.要证明两个三角形全等应有哪些必要条件?
(1)“SSS”:三边对应相等的两个三角形全等.
(2)“ASA”:两角和它们的夹边对应相等的两个三角形全等.
(3)“AAS”:两角和其中一角的对边对应相等的两个三角
形全等.
(4)“SAS”:两边和它们的夹角对应相等的两个三角形全等.
2.两个全等的三角形有哪些性质?
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等.
知识讲解
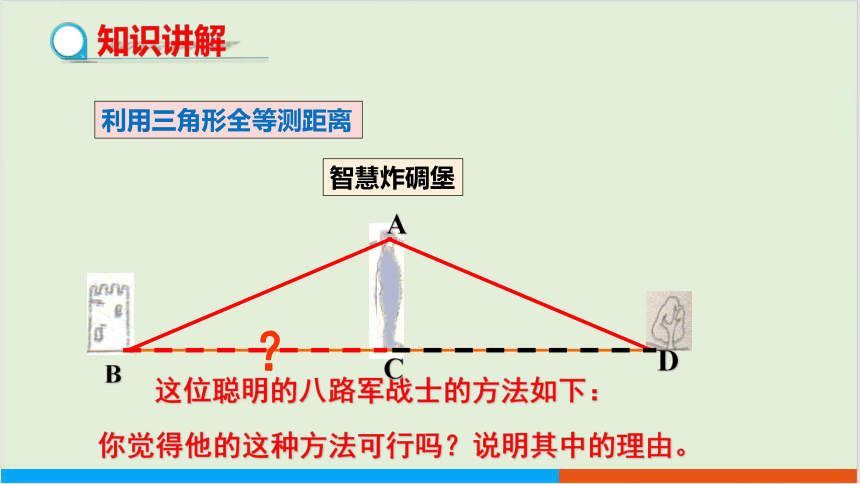
利用三角形全等测距离
智慧炸碉堡
这位聪明的八路军战士的方法如下:
A
C
B
D
?
你觉得他的这种方法可行吗?说明其中的理由。
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
你觉得他的这种方法可行吗?说明其中的理由。
( )
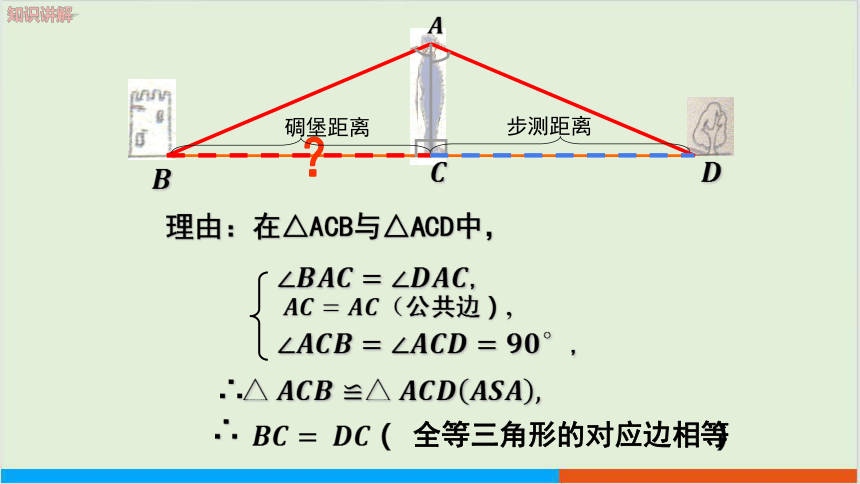
?
理由:在△ACB与△ACD中,
,
(公共边),
,
全等三角形的对应边相等
步测距离
碉堡距离
∴
∴
1、碉堡距离为什么等于步测距离?
?
步测距离
碉堡距离
2、这类题的关键是什么?
三角形全等
构建全等三角形
例 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,你能帮小明设计一个方案,解决此问题吗?
1.说出你的设计方案;
2.你能用所学知识说明你设计方案的理由是什么吗?
1.先在地上取一个可以直接到达点A和B的点C,连接AC并 延长到D,使AC=CD.
2.连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,测得DE的长度就是A、B 间的距离.
C
D
E
B
A
·
1.你能设计出其他的方案来吗?(构建全等三角形)
2.已知条件是什么?结论又是什么?
3.你能说明设计出方案的理由吗?
B
A
·
·
C
D
E
在△ABC与△DEC中,已知:AB⊥BE,DE⊥BE,BE=EC,结论:AB=DE.
·
所以AB = CD.
方
案
二
1
2
解:连结BD,因为AD∥CB,
所以∠1=∠2.
在△ABD与△CDB中,
如图,先作三角形,再找一点C,使BC∥AD,并使AD=BC,连结CD,量CD的长即得的长.
B
C
D
A
∠1=∠2,
AD=CB,
BD=DB,
所以△ABD≌△CDB(SAS)
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长.
解:连接AB.
在Rt△ADB与Rt△CDB中,
所以 △ADB≌△CDB(SAS),
所以BA=BC.
BD=BD,
∠ADB=∠CDB,
AD=CD,
方
案
三
1.如图,工人师傅要计算一个圆柱
形容器的容积,需要测量其内径.
现在有两根同样长的木棒、一条
橡皮绳和一把带有刻度的直尺,
你能想法帮助他完成吗?
·
中点C
A
B
练一练
2.一个人站在路中央,先往左看了看,又往右看了看,
然后说知道纪念碑相当于5层楼那么高,你知道他是
怎么做到的吗?
随堂训练
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS
B.ASA
C.AAS
D.SAS
B
A
●
●
D
C
E
F
B
2.如图所示小明设计了一种测工件内径AB的卡钳,问:
在卡钳的设计中,AO、BO、CO、DO 应满足下列
的哪个条件?( )
A. AO=CO
B. BO=DO
C. AC=BD
D. AO=CO且BO=DO
O
D
C
B
A
D
3.如图所示,已知AC=DB,AO=DO,CD=100 m,
则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
C
4.如图,公园里有一条“Z”字型道路ABCD,其中AB∥CD,在AB,BC,CD三段道路旁各有一只小石凳E,M,F,M恰为BC的中点,且E,M,F在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B,E之间的距离,你能想出解决的方法吗?请说明其中的道理.
解:因为AB∥CD,所以∠B=∠C.
在△BME和△CMF中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BME≌△CMF(ASA),所以BE=CF.
故只要测量CF即可得B,E之间的距离.
课堂小结
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
第 四章 三角形
第四章 三角形
5 利用三角形全等测距离
学 习 目 标
1.复习并归纳三角形全等的判定及性质;
2.能够根据三角形全等测定两点间的距离,并解
决实际问题.(重点,难点)
复习导入
1.要证明两个三角形全等应有哪些必要条件?
(1)“SSS”:三边对应相等的两个三角形全等.
(2)“ASA”:两角和它们的夹边对应相等的两个三角形全等.
(3)“AAS”:两角和其中一角的对边对应相等的两个三角
形全等.
(4)“SAS”:两边和它们的夹角对应相等的两个三角形全等.
2.两个全等的三角形有哪些性质?
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等.
知识讲解
利用三角形全等测距离
智慧炸碉堡
这位聪明的八路军战士的方法如下:
A
C
B
D
?
你觉得他的这种方法可行吗?说明其中的理由。
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
你觉得他的这种方法可行吗?说明其中的理由。
( )
?
理由:在△ACB与△ACD中,
,
(公共边),
,
全等三角形的对应边相等
步测距离
碉堡距离
∴
∴
1、碉堡距离为什么等于步测距离?
?
步测距离
碉堡距离
2、这类题的关键是什么?
三角形全等
构建全等三角形
例 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,你能帮小明设计一个方案,解决此问题吗?
1.说出你的设计方案;
2.你能用所学知识说明你设计方案的理由是什么吗?
1.先在地上取一个可以直接到达点A和B的点C,连接AC并 延长到D,使AC=CD.
2.连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,测得DE的长度就是A、B 间的距离.
C
D
E
B
A
·
1.你能设计出其他的方案来吗?(构建全等三角形)
2.已知条件是什么?结论又是什么?
3.你能说明设计出方案的理由吗?
B
A
·
·
C
D
E
在△ABC与△DEC中,已知:AB⊥BE,DE⊥BE,BE=EC,结论:AB=DE.
·
所以AB = CD.
方
案
二
1
2
解:连结BD,因为AD∥CB,
所以∠1=∠2.
在△ABD与△CDB中,
如图,先作三角形,再找一点C,使BC∥AD,并使AD=BC,连结CD,量CD的长即得的长.
B
C
D
A
∠1=∠2,
AD=CB,
BD=DB,
所以△ABD≌△CDB(SAS)
如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长.
解:连接AB.
在Rt△ADB与Rt△CDB中,
所以 △ADB≌△CDB(SAS),
所以BA=BC.
BD=BD,
∠ADB=∠CDB,
AD=CD,
方
案
三
1.如图,工人师傅要计算一个圆柱
形容器的容积,需要测量其内径.
现在有两根同样长的木棒、一条
橡皮绳和一把带有刻度的直尺,
你能想法帮助他完成吗?
·
中点C
A
B
练一练
2.一个人站在路中央,先往左看了看,又往右看了看,
然后说知道纪念碑相当于5层楼那么高,你知道他是
怎么做到的吗?
随堂训练
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS
B.ASA
C.AAS
D.SAS
B
A
●
●
D
C
E
F
B
2.如图所示小明设计了一种测工件内径AB的卡钳,问:
在卡钳的设计中,AO、BO、CO、DO 应满足下列
的哪个条件?( )
A. AO=CO
B. BO=DO
C. AC=BD
D. AO=CO且BO=DO
O
D
C
B
A
D
3.如图所示,已知AC=DB,AO=DO,CD=100 m,
则A,B两点间的距离( )
A.大于100 m B.等于100 m
C.小于100 m D.无法确定
C
4.如图,公园里有一条“Z”字型道路ABCD,其中AB∥CD,在AB,BC,CD三段道路旁各有一只小石凳E,M,F,M恰为BC的中点,且E,M,F在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B,E之间的距离,你能想出解决的方法吗?请说明其中的道理.
解:因为AB∥CD,所以∠B=∠C.
在△BME和△CMF中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BME≌△CMF(ASA),所以BE=CF.
故只要测量CF即可得B,E之间的距离.
课堂小结
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
