3.2图形的旋转(第2课时)教学详案--北师大版初中数学八年级(下)
文档属性
| 名称 | 3.2图形的旋转(第2课时)教学详案--北师大版初中数学八年级(下) |

|
|
| 格式 | docx | ||
| 文件大小 | 820.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:11 | ||
图片预览


文档简介
3.2 图形的旋转(第2课时 旋转作图)
教学目标
1.进一步理解并掌握旋转的意义和性质.
2.能够根据旋转的性质作出一些简单的平面图形旋转后的图形.
3.能够综合运用平移和旋转分析、解释一些简单图形的变换.
教学重点难点
重点:根据旋转的性质作出一些简单的平面图形旋转后的图形.
难点:综合运用平移和旋转分析、解释一些简单图形的变换.
教学过程
复习巩固
1.旋转:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.
2.旋转的性质:
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.
导入新课
我们学习了旋转的定义与性质,你能准确地找到一个图形绕点旋转后的位置,进而作出它旋转后的图形吗?这是本节课学习的内容.
探究新知
探究点一:旋转作图
类型一:简单的旋转作图
活动1 动手操作
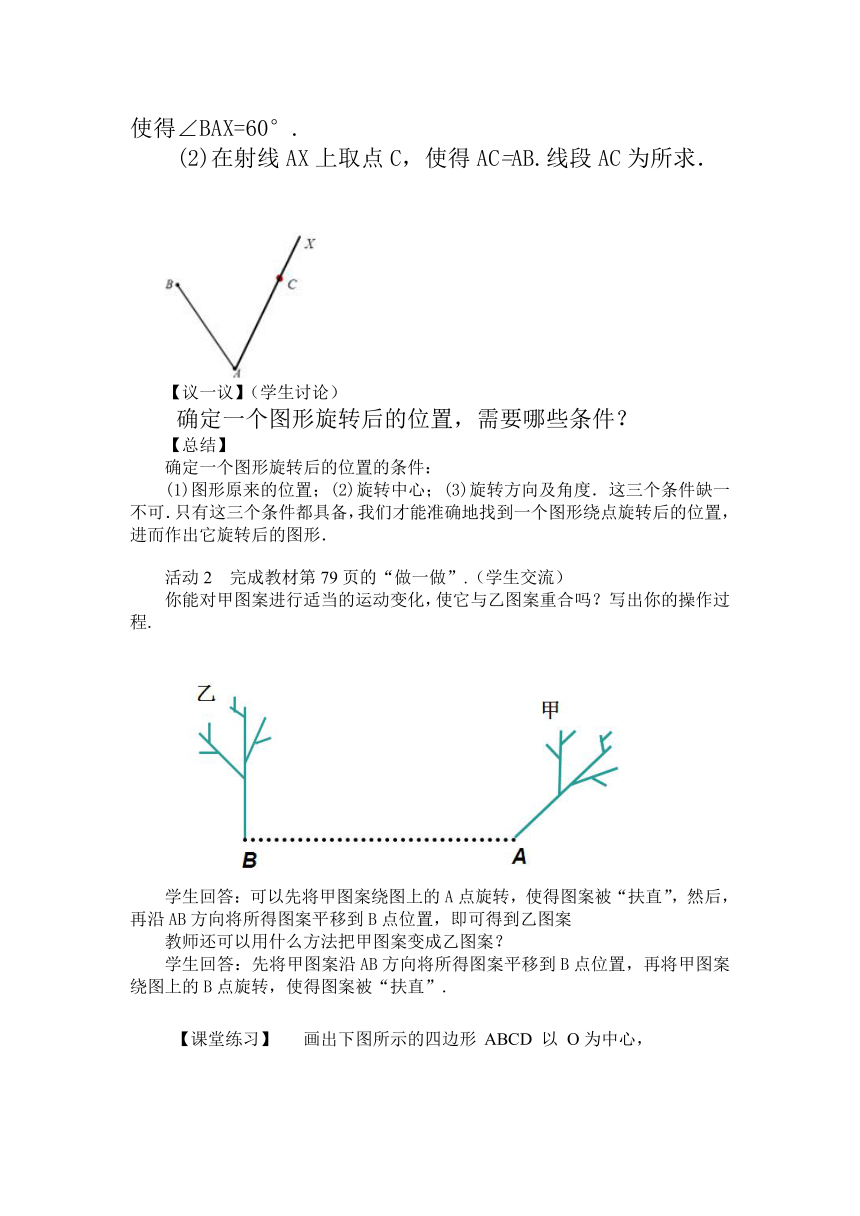
【画一画】如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
【议一议】(学生讨论)
确定一个图形旋转后的位置,需要哪些条件?
【总结】
确定一个图形旋转后的位置的条件:
(1)图形原来的位置;(2)旋转中心;(3)旋转方向及角度.这三个条件缺一不可.只有这三个条件都具备,我们才能准确地找到一个图形绕点旋转后的位置,进而作出它旋转后的图形.
活动2 完成教材第79页的“做一做”.(学生交流)
你能对甲图案进行适当的运动变化,使它与乙图案重合吗?写出你的操作过程.
学生回答:可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
教师还可以用什么方法把甲图案变成乙图案?
学生回答:先将甲图案沿AB方向将所得图案平移到B点位置,再将甲图案绕图上的B点旋转,使得图案被“扶直”.
【课堂练习】 画出下图所示的四边形 ABCD 以 O为中心,
旋转角都为 60°的旋转图形.
参考答案
【总结】
旋转作图一般步骤:
(1)找:分析题目要求,找出旋转中心、旋转角以及构成图形的关键点;
(2)连:连接图形中每一个关键点与旋转中心;
(3)转:把连线绕旋转中心按旋转方向分别旋转相同的角度(旋转角的度数);
(4)截:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点;
(5)作:按原图顺序依次连接各个关键点的对应点,并标上相应的字母;
(6)写:写出结论.
活动3 探究应用 (教师引导,学生互学)
【例1】
将一个直角三角板绕30°角的顶点顺时针旋转,使一直角边与原斜边在同一条直线上(如图所示).你知道旋转角是多少吗?连接BB′,△ABB′有什么特征?
解:由旋转可知,旋转角为∠BAB′,它的度数为180°-30°=150°. 连接BB′,△ABB′为顶角为150°的等腰三角形.
活动4 拓展提升
类型二:直角坐标系中的旋转作图
【例2】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
【探索分析】(引发学生思考)(1)根据网格结构找出点A、B、C旋转180°后的对应点A1、B1、C1的位置,然后顺次连接即可.找出平移后的对应点A2、B2、C2的位置,然后顺次连接即可.
(2)根据旋转的定义结合图形,连接两对对应点,交点即为旋转中心.
【解】(1)△A1B1C1、△A2B2C2如图所示.
(2)如上图,旋转中心为.
【题后总结】(学生总结,老师点评)本题考查了利用旋转变换和轴对称变换作图,熟练掌握网格结构,准确找出对应点的位置是解题关键.
活动5 小组讨论
探究点二:平移、旋转的异同
【问题】(学生交流)
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗 能经过平移吗 能经过轴对称吗 还有其他方式吗
思考:1.平移的两个要素:
平移的方向,平移的距离
2.旋转的三要素:
旋转中心、旋转方向、旋转角
回答:整个图形可以看作是左边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的.
【总结】
相同:都是一种运动;运动前后不改变图形的形状和大小.
不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
活动2 【课堂练习】
1.△ABC是等腰直角三角形,其中∠ACB是直角,将△ABC绕着点A逆时针旋转45°,旋转前后的图形组成图1;再将图1作为“基本图形”绕着点A经过逆时针连续旋转得到图2.三次旋转的角度分别为( )
A.90°,180°,270° B.90°,45°,180°
C.60°,30°,90° D.30°,60°,180°
2.下列选项中,甲图案变成乙图案,既能用平移,又能用旋转的是( )
A.
B.
C.
D.
3. 如图,四边形ABCD绕O点旋转后,顶点A的对应点
为E,试确定B、C、D对应的点的位置,以及旋转
后的四边形.
参考答案:
1.A 解析:将△ABC绕着点A逆时针旋转45°,旋转前后的图形组成图1;再将图1作为“基本图形”绕着点A经过逆时针连续旋转得到图2.三次旋转的角度分别为 90°,180°,270°.
2. B 解析:A.甲图案变成乙图案只能用轴对称,不能用平移、旋转,错误;B.甲图案变成乙图案既能用平移,又能用旋转,正确;C.甲图案变成乙图案只能用轴对称,不能用平移、旋转,错误;D.甲图案变成乙图案只能用平移,不能用旋转,错误.故选B.
3. 解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,
使∠BOF = ∠COG= ∠DOH = ∠AOE;
(3)分别在射线OF ,OG ,OH上,截取OF=OB ,OG=OC,OH=OD;
(4)连接EF ,FG ,GH ,HE ,
所以四边形EFGH就是四边形ABCD绕O点旋转后的图形.
课堂小结
(学生总结,老师点评)
旋转作图一般步骤
(1)明确旋转三要素:
旋转中心、旋转方向和旋转角度.
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
布置作业
教材第79页习题3.5
板书设计
2图形的旋转
一、旋转作图
简单图形的旋转作图
直角坐标系中的旋转作图
旋转作图一般步骤
二、平移与旋转的异同
教学目标
1.进一步理解并掌握旋转的意义和性质.
2.能够根据旋转的性质作出一些简单的平面图形旋转后的图形.
3.能够综合运用平移和旋转分析、解释一些简单图形的变换.
教学重点难点
重点:根据旋转的性质作出一些简单的平面图形旋转后的图形.
难点:综合运用平移和旋转分析、解释一些简单图形的变换.
教学过程
复习巩固
1.旋转:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.
2.旋转的性质:
一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.
导入新课
我们学习了旋转的定义与性质,你能准确地找到一个图形绕点旋转后的位置,进而作出它旋转后的图形吗?这是本节课学习的内容.
探究新知
探究点一:旋转作图
类型一:简单的旋转作图
活动1 动手操作
【画一画】如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
【议一议】(学生讨论)
确定一个图形旋转后的位置,需要哪些条件?
【总结】
确定一个图形旋转后的位置的条件:
(1)图形原来的位置;(2)旋转中心;(3)旋转方向及角度.这三个条件缺一不可.只有这三个条件都具备,我们才能准确地找到一个图形绕点旋转后的位置,进而作出它旋转后的图形.
活动2 完成教材第79页的“做一做”.(学生交流)
你能对甲图案进行适当的运动变化,使它与乙图案重合吗?写出你的操作过程.
学生回答:可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
教师还可以用什么方法把甲图案变成乙图案?
学生回答:先将甲图案沿AB方向将所得图案平移到B点位置,再将甲图案绕图上的B点旋转,使得图案被“扶直”.
【课堂练习】 画出下图所示的四边形 ABCD 以 O为中心,
旋转角都为 60°的旋转图形.
参考答案
【总结】
旋转作图一般步骤:
(1)找:分析题目要求,找出旋转中心、旋转角以及构成图形的关键点;
(2)连:连接图形中每一个关键点与旋转中心;
(3)转:把连线绕旋转中心按旋转方向分别旋转相同的角度(旋转角的度数);
(4)截:沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点;
(5)作:按原图顺序依次连接各个关键点的对应点,并标上相应的字母;
(6)写:写出结论.
活动3 探究应用 (教师引导,学生互学)
【例1】
将一个直角三角板绕30°角的顶点顺时针旋转,使一直角边与原斜边在同一条直线上(如图所示).你知道旋转角是多少吗?连接BB′,△ABB′有什么特征?
解:由旋转可知,旋转角为∠BAB′,它的度数为180°-30°=150°. 连接BB′,△ABB′为顶角为150°的等腰三角形.
活动4 拓展提升
类型二:直角坐标系中的旋转作图
【例2】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
【探索分析】(引发学生思考)(1)根据网格结构找出点A、B、C旋转180°后的对应点A1、B1、C1的位置,然后顺次连接即可.找出平移后的对应点A2、B2、C2的位置,然后顺次连接即可.
(2)根据旋转的定义结合图形,连接两对对应点,交点即为旋转中心.
【解】(1)△A1B1C1、△A2B2C2如图所示.
(2)如上图,旋转中心为.
【题后总结】(学生总结,老师点评)本题考查了利用旋转变换和轴对称变换作图,熟练掌握网格结构,准确找出对应点的位置是解题关键.
活动5 小组讨论
探究点二:平移、旋转的异同
【问题】(学生交流)
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗 能经过平移吗 能经过轴对称吗 还有其他方式吗
思考:1.平移的两个要素:
平移的方向,平移的距离
2.旋转的三要素:
旋转中心、旋转方向、旋转角
回答:整个图形可以看作是左边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的.
【总结】
相同:都是一种运动;运动前后不改变图形的形状和大小.
不同
图形变换 运动方向 运动量的衡量
平移 直线 移动一定距离
旋转 顺时针或逆时针 转动一定的角度
活动2 【课堂练习】
1.△ABC是等腰直角三角形,其中∠ACB是直角,将△ABC绕着点A逆时针旋转45°,旋转前后的图形组成图1;再将图1作为“基本图形”绕着点A经过逆时针连续旋转得到图2.三次旋转的角度分别为( )
A.90°,180°,270° B.90°,45°,180°
C.60°,30°,90° D.30°,60°,180°
2.下列选项中,甲图案变成乙图案,既能用平移,又能用旋转的是( )
A.
B.
C.
D.
3. 如图,四边形ABCD绕O点旋转后,顶点A的对应点
为E,试确定B、C、D对应的点的位置,以及旋转
后的四边形.
参考答案:
1.A 解析:将△ABC绕着点A逆时针旋转45°,旋转前后的图形组成图1;再将图1作为“基本图形”绕着点A经过逆时针连续旋转得到图2.三次旋转的角度分别为 90°,180°,270°.
2. B 解析:A.甲图案变成乙图案只能用轴对称,不能用平移、旋转,错误;B.甲图案变成乙图案既能用平移,又能用旋转,正确;C.甲图案变成乙图案只能用轴对称,不能用平移、旋转,错误;D.甲图案变成乙图案只能用平移,不能用旋转,错误.故选B.
3. 解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,
使∠BOF = ∠COG= ∠DOH = ∠AOE;
(3)分别在射线OF ,OG ,OH上,截取OF=OB ,OG=OC,OH=OD;
(4)连接EF ,FG ,GH ,HE ,
所以四边形EFGH就是四边形ABCD绕O点旋转后的图形.
课堂小结
(学生总结,老师点评)
旋转作图一般步骤
(1)明确旋转三要素:
旋转中心、旋转方向和旋转角度.
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
布置作业
教材第79页习题3.5
板书设计
2图形的旋转
一、旋转作图
简单图形的旋转作图
直角坐标系中的旋转作图
旋转作图一般步骤
二、平移与旋转的异同
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
