3.3轴对称和平移的坐标表示(第2课时 平移的坐标表示) 教学课件--湘教版数学八年级(下)
文档属性
| 名称 | 3.3轴对称和平移的坐标表示(第2课时 平移的坐标表示) 教学课件--湘教版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第3章 图形与坐标
3.3 轴对称和平移的坐标表示
第3章 图形与坐标
第2课时 平移的坐标表示
学 习 目 标
1
2
掌握图形在平面直角坐标系中平移前后点的坐标的变化规律;
体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念.
3
用点的坐标变化表示图形的平移;
复习巩固
如图,数轴上点表示的数是 ,点A 向右平移两个单位后表示的数是 .点B表示的数是 ,点B向左平移3个单位后表示的数是 .
从数轴上的点的平移你发现了什么?说出来与大家分享你的重大发现.
-3
-1
1
-2
新课导入
问题 你会下象棋吗 如果下一步红棋下“马走日”,你觉得应该走到哪里呢?
知识讲解
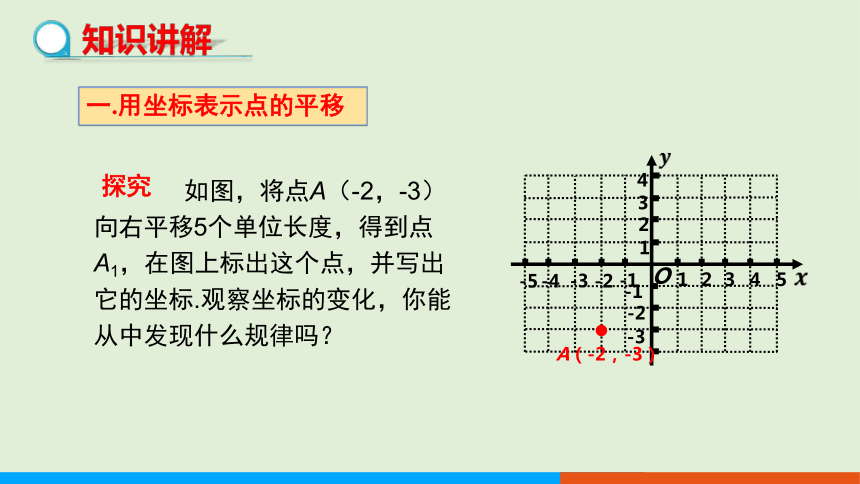
如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.观察坐标的变化,你能从中发现什么规律吗?
探究
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
一.用坐标表示点的平移
A1(3,-3)
观察点A,点A1的坐标可以发现:点A1的横坐标等于点A的横坐标加5, 点A1的纵坐标等于点A的纵坐标.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
把点A向上平移4个单位长度呢?
点A2的纵坐标等于点A的纵坐标加4,点A2的横坐标等于点A的横坐标.
A2(-2,1)
把点A向左或向下平移呢?再找几个点,对它们进行平移,观察它们的坐标是否按你发现的规律而变化?
变化规律仍然成立.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
(1)在平面直角坐标系中,将点(,)向右(或左)平移个单位长度,可以得到对应点的坐标是() 或( ,) ;
(2)将点()向上(或下)平移个单位长度,可以得到对应点的坐标是()或().
左右平移→左减右加纵不变
上下平移→上加下减横不变
归纳
平面直角坐标系中,将点A(-3,-5)向上平移4个 单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向
左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
例1
C
如图,ABC 在坐标平面内平移后得到新图形A1B1C1.
(1)移动的方向怎样?
向左平移了5个单位.
(2)写出ABC与A1B1C1各顶点坐标.比较对应点的坐标,看有怎样的变化?
A(2,7)
B(0,5)
C(4,1)
A1(-3,7)
B1(-5,5)
C1(-1,1)
向左平移了5个单位
横坐标减5,
纵坐标不变
二.图形左右平移时点的坐标变化
ABC 在坐标平面内平移后得到新图形A1B1C1.如果把ABC向右平移2个单位,得到A2B2C2.
写出这时各顶点 坐标,比较两者对应点坐标,看有怎样的变化.
A(2,7)
B(0,5)
C(4,1)
向右平移
了2个单位
横坐标加2,
纵坐标不变
A2(4,7)
B2(2,5)
C2(6,1)
A1(-3,7)
B1(-5,5)
C1(-1,1)
A(2,7)
B(0,5)
C(4,1)
向左平移了5个单位.
横坐标减5,
纵坐标不变
A2(4,7)
B2(2,5)
C2(6,1)
向右平移了2个单位.
横坐标加2,
纵坐标不变
总结与归纳:观察上面数据,你发现了什么?
点左右平移时,横坐标”左减右加“,纵坐标不变.
思考1:把平面直角坐标系中的一个图形,向左或向右移动(>0)个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
左右移动()个单位
横坐标改变,纵坐标不变
左减
右加
如果ABC向下平移2个单位,得到A1B1C1.
O
2
4
-2
-4
-2
2
4
6
8
A
B
C
A1
B1
写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化.
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
A(2,7)
B(0,5)
C(4,1)
三.图形上下平移时点的坐标变化
C1
写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化.
O
x
y
2
4
-2
-4
-2
2
4
6
8
A
B
C
A(2,7)
B(0,5)
C(4,1)
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
A2
B2
C2
A2(2,8)
B2(0,6)
C2(4,2)
向上平移了1个单位.
横坐标不变,
纵坐标加1
如果ABC向上平移1个单位,得到A2B2C2.
A(2,7)
B(0,5)
C(4,1)
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
向上平移了1个单位.
横坐标不变,
纵坐标加1
总结与归纳:观察上面数据,你发现了什么?
A2(2,8)
B2(0,6)
C2(4,2)
点上下平移时,横坐标不变,纵坐标“上加下减“.
思考 2:把平面直角坐标系中的一个图形,向上或向下移动个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
上下移动个单位
横坐标不变,纵坐标改变
上加
下减
思考 3:把平面直角坐标系中的一个图形,向左或向右移动个单位,再向上或向下移动个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
先向左平移个单位 , 再向上平移个单位
先向左平移个单位 , 再向下平移个单位
先向右平移个单位 , 再向上平移个单位
先向右平移个单位 , 再向下平移个单位
例 2 如图,将ABC先向右平移6个单位,再向下平移2个单位得到A1B1C1,写出各顶点变动前后的坐标.
解:
用箭头代表平移,有
A(-2,6)
(4,6)
A1(4,4)
B(-4,4)
(2,4)
B1(2,2)
C(1,1)
(7,1)
C1(7,-1)
1.线段AB两端点的坐标分别为A(-1,4),B(-4,1),现将它向左平移4个单位长度,得到线段A1B1,则点A1,B1的坐标分别为( )
A.A1(3,4),B1(0,1)
B.A1(-5,4),B1(-8,1)
C.A1(3,7),B1(0,5)
D.A1(-5,0),B1(-8,-3)
B
随堂训练
2.下面每个图形中的图 是由图 平移得到的,描述各图是如何移动的,并写出图 、图 各定点的坐标.
图②是由图①先向下平移6个单位,再向右平移5个单位得到的.
图①各顶点的坐标分别为;
图②各顶点的坐标分别为
3.如图,已知ABC,经下列平移后,求它的顶点的坐标.
(1)右移2个单位,再下移1个单位;
A(2,1),B(1,-1),C(5,-2) .
(2)左移3个单位,再上移4个单位;
A(-3,6),B(-4,4),C(0,3) .
4.写出点P(4,5)在作出下列平移后得到的点P1的坐标,并说出点P到点P1是怎样平移的.
(1) P()→P1();
(2) P()→P1();
解:(1)P(4,5)→P1(5,7);
(2)P(4,5)→P1(1,4);
点P先向右平移1个单位,再向上平移2个单位得到点P1.
点先向左平移3个单位,再向下平移1个单位得到点P1.
5.如图,A′B′C′是由ABC平移得到的,已知ABC中任意一点)经平移后的对应点为P′().
(1)试说明A′B′C′是如何由ABC平移得到的.
解:根据对应点坐标平移的规律即可得出:
ABC先向右平移5个单位,
再向下平移2个单位得到A′B′C′.
(2)已知点A(-1,2),B(-4,5),C(-3,0),请写出点A′,B′,C′ 的坐标;
点A′ 的坐标为(4,0),
点B′ 的坐标为(1,3),
点C′ 的坐标为(2,-2).
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
第3章 图形与坐标
3.3 轴对称和平移的坐标表示
第3章 图形与坐标
第2课时 平移的坐标表示
学 习 目 标
1
2
掌握图形在平面直角坐标系中平移前后点的坐标的变化规律;
体会平面直角坐标系是数与形之间的桥梁,感受代数与几何的相互转化,初步建立空间概念.
3
用点的坐标变化表示图形的平移;
复习巩固
如图,数轴上点表示的数是 ,点A 向右平移两个单位后表示的数是 .点B表示的数是 ,点B向左平移3个单位后表示的数是 .
从数轴上的点的平移你发现了什么?说出来与大家分享你的重大发现.
-3
-1
1
-2
新课导入
问题 你会下象棋吗 如果下一步红棋下“马走日”,你觉得应该走到哪里呢?
知识讲解
如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.观察坐标的变化,你能从中发现什么规律吗?
探究
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
一.用坐标表示点的平移
A1(3,-3)
观察点A,点A1的坐标可以发现:点A1的横坐标等于点A的横坐标加5, 点A1的纵坐标等于点A的纵坐标.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
把点A向上平移4个单位长度呢?
点A2的纵坐标等于点A的纵坐标加4,点A2的横坐标等于点A的横坐标.
A2(-2,1)
把点A向左或向下平移呢?再找几个点,对它们进行平移,观察它们的坐标是否按你发现的规律而变化?
变化规律仍然成立.
1
1
-1
-2
-3
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
O
A(-2,-3)
(1)在平面直角坐标系中,将点(,)向右(或左)平移个单位长度,可以得到对应点的坐标是() 或( ,) ;
(2)将点()向上(或下)平移个单位长度,可以得到对应点的坐标是()或().
左右平移→左减右加纵不变
上下平移→上加下减横不变
归纳
平面直角坐标系中,将点A(-3,-5)向上平移4个 单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向
左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
例1
C
如图,ABC 在坐标平面内平移后得到新图形A1B1C1.
(1)移动的方向怎样?
向左平移了5个单位.
(2)写出ABC与A1B1C1各顶点坐标.比较对应点的坐标,看有怎样的变化?
A(2,7)
B(0,5)
C(4,1)
A1(-3,7)
B1(-5,5)
C1(-1,1)
向左平移了5个单位
横坐标减5,
纵坐标不变
二.图形左右平移时点的坐标变化
ABC 在坐标平面内平移后得到新图形A1B1C1.如果把ABC向右平移2个单位,得到A2B2C2.
写出这时各顶点 坐标,比较两者对应点坐标,看有怎样的变化.
A(2,7)
B(0,5)
C(4,1)
向右平移
了2个单位
横坐标加2,
纵坐标不变
A2(4,7)
B2(2,5)
C2(6,1)
A1(-3,7)
B1(-5,5)
C1(-1,1)
A(2,7)
B(0,5)
C(4,1)
向左平移了5个单位.
横坐标减5,
纵坐标不变
A2(4,7)
B2(2,5)
C2(6,1)
向右平移了2个单位.
横坐标加2,
纵坐标不变
总结与归纳:观察上面数据,你发现了什么?
点左右平移时,横坐标”左减右加“,纵坐标不变.
思考1:把平面直角坐标系中的一个图形,向左或向右移动(>0)个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
左右移动()个单位
横坐标改变,纵坐标不变
左减
右加
如果ABC向下平移2个单位,得到A1B1C1.
O
2
4
-2
-4
-2
2
4
6
8
A
B
C
A1
B1
写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化.
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
A(2,7)
B(0,5)
C(4,1)
三.图形上下平移时点的坐标变化
C1
写出这时各顶点坐标,比较两者对应点坐标,看有怎样的变化.
O
x
y
2
4
-2
-4
-2
2
4
6
8
A
B
C
A(2,7)
B(0,5)
C(4,1)
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
A2
B2
C2
A2(2,8)
B2(0,6)
C2(4,2)
向上平移了1个单位.
横坐标不变,
纵坐标加1
如果ABC向上平移1个单位,得到A2B2C2.
A(2,7)
B(0,5)
C(4,1)
A1(2,5)
B1(0,3)
C1(4,-1)
向下平移了2个单位.
横坐标不变,
纵坐标减2
向上平移了1个单位.
横坐标不变,
纵坐标加1
总结与归纳:观察上面数据,你发现了什么?
A2(2,8)
B2(0,6)
C2(4,2)
点上下平移时,横坐标不变,纵坐标“上加下减“.
思考 2:把平面直角坐标系中的一个图形,向上或向下移动个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
上下移动个单位
横坐标不变,纵坐标改变
上加
下减
思考 3:把平面直角坐标系中的一个图形,向左或向右移动个单位,再向上或向下移动个单位,那么图形上任何一个点的坐标()是如何变化的?
点()
先向左平移个单位 , 再向上平移个单位
先向左平移个单位 , 再向下平移个单位
先向右平移个单位 , 再向上平移个单位
先向右平移个单位 , 再向下平移个单位
例 2 如图,将ABC先向右平移6个单位,再向下平移2个单位得到A1B1C1,写出各顶点变动前后的坐标.
解:
用箭头代表平移,有
A(-2,6)
(4,6)
A1(4,4)
B(-4,4)
(2,4)
B1(2,2)
C(1,1)
(7,1)
C1(7,-1)
1.线段AB两端点的坐标分别为A(-1,4),B(-4,1),现将它向左平移4个单位长度,得到线段A1B1,则点A1,B1的坐标分别为( )
A.A1(3,4),B1(0,1)
B.A1(-5,4),B1(-8,1)
C.A1(3,7),B1(0,5)
D.A1(-5,0),B1(-8,-3)
B
随堂训练
2.下面每个图形中的图 是由图 平移得到的,描述各图是如何移动的,并写出图 、图 各定点的坐标.
图②是由图①先向下平移6个单位,再向右平移5个单位得到的.
图①各顶点的坐标分别为;
图②各顶点的坐标分别为
3.如图,已知ABC,经下列平移后,求它的顶点的坐标.
(1)右移2个单位,再下移1个单位;
A(2,1),B(1,-1),C(5,-2) .
(2)左移3个单位,再上移4个单位;
A(-3,6),B(-4,4),C(0,3) .
4.写出点P(4,5)在作出下列平移后得到的点P1的坐标,并说出点P到点P1是怎样平移的.
(1) P()→P1();
(2) P()→P1();
解:(1)P(4,5)→P1(5,7);
(2)P(4,5)→P1(1,4);
点P先向右平移1个单位,再向上平移2个单位得到点P1.
点先向左平移3个单位,再向下平移1个单位得到点P1.
5.如图,A′B′C′是由ABC平移得到的,已知ABC中任意一点)经平移后的对应点为P′().
(1)试说明A′B′C′是如何由ABC平移得到的.
解:根据对应点坐标平移的规律即可得出:
ABC先向右平移5个单位,
再向下平移2个单位得到A′B′C′.
(2)已知点A(-1,2),B(-4,5),C(-3,0),请写出点A′,B′,C′ 的坐标;
点A′ 的坐标为(4,0),
点B′ 的坐标为(1,3),
点C′ 的坐标为(2,-2).
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
