5.2 探索轴对称的性质教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 5.2 探索轴对称的性质教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:07:33 | ||
图片预览




文档简介
(共28张PPT)
第五章 生活中的轴对称
第五章 生活中的轴对称
5.2探索轴对称的性质
学 习 目 标
1
2
探索并掌握轴对称的性质. (重点)
会利用轴对称的性质作对称点、对称图形、对称轴等. (难点)
1、轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫作轴对称图形.这条直线叫这个图形的对称轴.
2、轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称.这条直线就是对称轴.
知识回顾
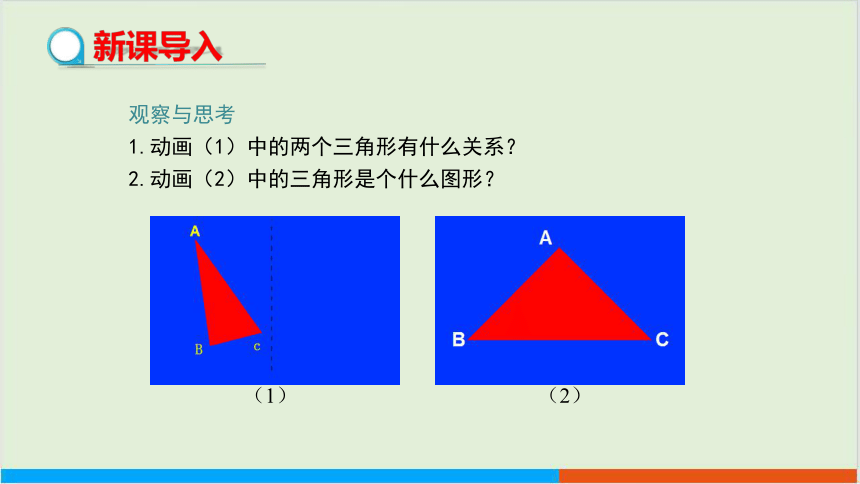
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
新课导入
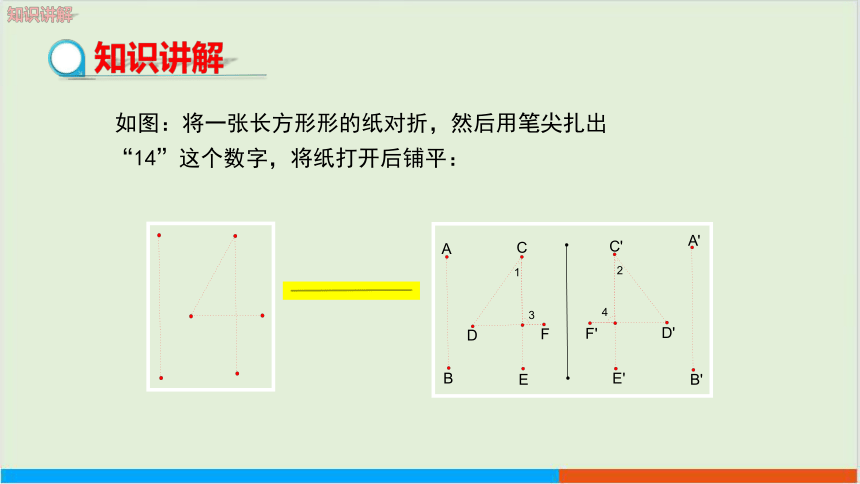
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
知识讲解
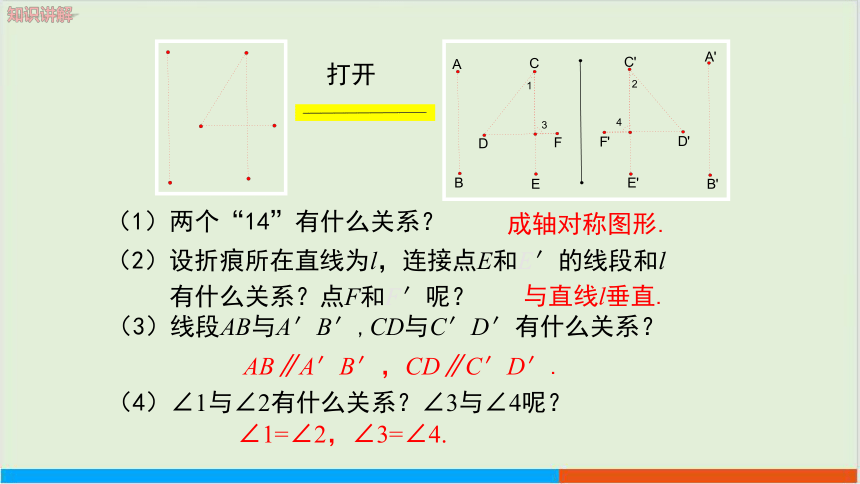
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l
有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
与直线l垂直.
AB∥A′B′,CD∥C′D′.
∠1=∠2,∠3=∠4.
成轴对称图形.
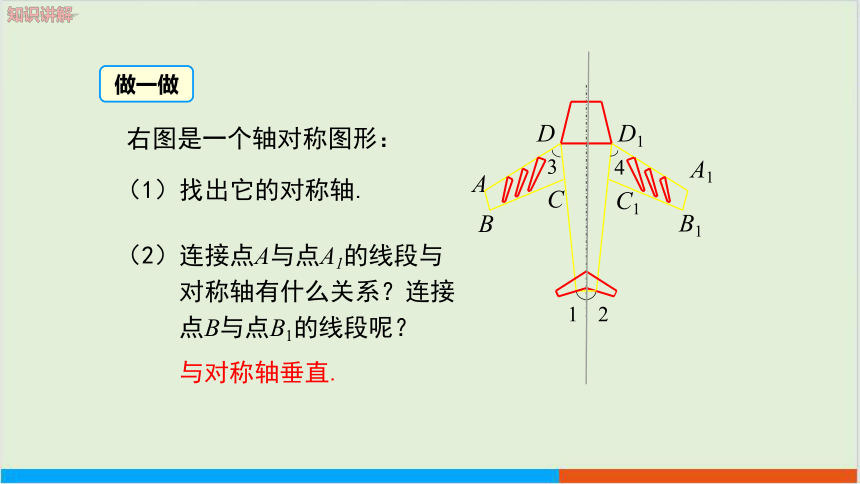
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与
对称轴有什么关系?连接
点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
做一做
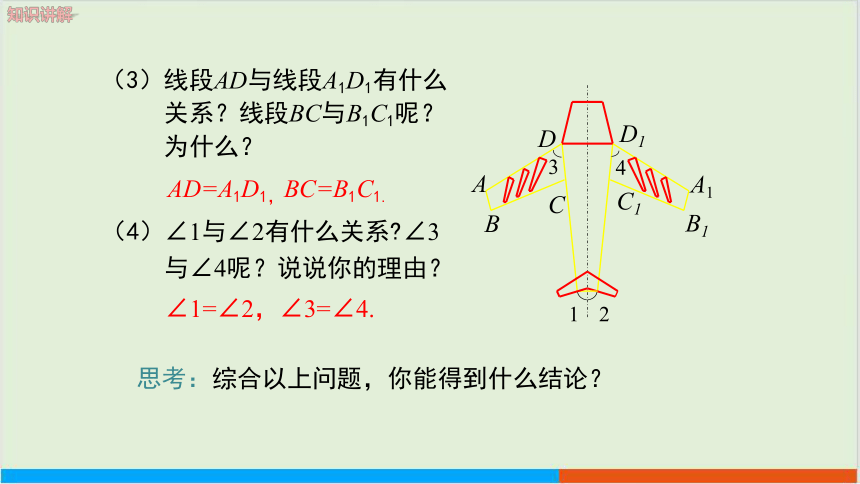
(3)线段AD与线段A1D1有什么
关系?线段BC与B1C1呢?
为什么?
(4)∠1与∠2有什么关系 ∠3
与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
思考:综合以上问题,你能得到什么结论?
A
A1
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
总结归纳
图5-7是一个图案的一半,其中的
虚线是这个图案的对称轴,画出这个
图案的另一半.
做一做
例1 画出△ABC关于直线l的对称图形.
解:如图所示.
方法总结:先确定一些特殊的点,然后作这些
特殊点的对称点,顺次连接即可.
例题讲解
例2 如图,一种滑翔伞的形状是左右成轴对称
的四边形ABCD,其中∠BAD=150°,∠B=40°,
则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
解析:∵这种滑翔伞的形状是左右成轴对称的
四边形ABCD,其中∠BAD=150°,∠B=40°,∴∠D=40°,∴∠BCD=360°-150°-40°-40°=130°.
A
例3 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).故选B.
B
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
1.如果两个图形关于某条直线对称,那么对应点所
连的线段被__________垂直平分.
2.下图是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
对称轴
AB=CD,
BE=CE
∠B=∠C
随堂训练
3.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
解析:由轴对称的性质可得∠A1=∠A=50°, ∠C=∠C1=30°,所以∠B=∠B1=180°-50°-30°=100°.
100°
4.下面两个轴对称图形分别只画出了一半,请画
出它们的另一半(直线L为对称轴).
解:如图所示.
1.如图,已知点A、B直线MN同侧两点,点A1、A
关于直线MN对称.连接A1B交直线MN于点P,连
接AP.
(1)若A1B=5cm,则AP+BP的长为 .
5cm
A
B
P
A1
N
M
拓展提升
(2)某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B.为了节约资金,使修建的水渠最短,应将缺口P修建在哪里 请你利用所学知识解决这一问题,并用红色线段画出水渠.
A
B
P
M
N
A
B
M
A1
2.如图,已知点P是∠AOB内任意一点,点P1,P
关于OA对称,点P2,P关于OB对称.连接P1P2,分
别交OA,OB于C, D.连接PC,PD.若P1P2=10cm,
则△PCD的周长为 .
10cm
.
.
P2
P
.
P1
C
D
B
A
O
课堂小结
轴对称的性质
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
1.如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
解析:△HEC关于CD对称;△FDB关于BE对称;△GED关于HF对称;关于AG对称的是它本身.所以共3个.故选C.
当堂检测
2.作△ABC关于直线l对称的△A′B′C′,点A,B,C的对称点分别是A′,B′,C′,则下列说法中正确的是( )
A. AA′垂直平分对称轴
B. △ABC和△A′B′C′的周长相等
C. 线段AB′被对称轴平分
D. △ABC的面积被对称轴平分
B
3.如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B= .
解析:∵△ABC 与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,∴∠C=∠C′=60°,
∵∠A=30°,∴∠B=180°-∠A-∠C=180°-30°-60°=90°.
故答案为:90°.
90°
5.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
第五章 生活中的轴对称
第五章 生活中的轴对称
5.2探索轴对称的性质
学 习 目 标
1
2
探索并掌握轴对称的性质. (重点)
会利用轴对称的性质作对称点、对称图形、对称轴等. (难点)
1、轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫作轴对称图形.这条直线叫这个图形的对称轴.
2、轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称.这条直线就是对称轴.
知识回顾
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
新课导入
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
知识讲解
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l
有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
与直线l垂直.
AB∥A′B′,CD∥C′D′.
∠1=∠2,∠3=∠4.
成轴对称图形.
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与
对称轴有什么关系?连接
点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
做一做
(3)线段AD与线段A1D1有什么
关系?线段BC与B1C1呢?
为什么?
(4)∠1与∠2有什么关系 ∠3
与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
思考:综合以上问题,你能得到什么结论?
A
A1
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
总结归纳
图5-7是一个图案的一半,其中的
虚线是这个图案的对称轴,画出这个
图案的另一半.
做一做
例1 画出△ABC关于直线l的对称图形.
解:如图所示.
方法总结:先确定一些特殊的点,然后作这些
特殊点的对称点,顺次连接即可.
例题讲解
例2 如图,一种滑翔伞的形状是左右成轴对称
的四边形ABCD,其中∠BAD=150°,∠B=40°,
则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
解析:∵这种滑翔伞的形状是左右成轴对称的
四边形ABCD,其中∠BAD=150°,∠B=40°,∴∠D=40°,∴∠BCD=360°-150°-40°-40°=130°.
A
例3 如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
解析:根据正方形的轴对称性可得,阴影部分的面积等于正方形ABCD面积的一半,∵正方形ABCD的边长为4cm,∴S阴影=42÷2=8(cm2).故选B.
B
方法归纳:正方形是轴对称图形,在轴对称图形中求不规则的阴影部分的面积时,一般可以利用轴对称变换,将其转换为规则图形后再进行计算.
1.如果两个图形关于某条直线对称,那么对应点所
连的线段被__________垂直平分.
2.下图是轴对称图形,相等的线段是____________
________,相等的角是__________.
A
B
C
D
E
对称轴
AB=CD,
BE=CE
∠B=∠C
随堂训练
3.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
解析:由轴对称的性质可得∠A1=∠A=50°, ∠C=∠C1=30°,所以∠B=∠B1=180°-50°-30°=100°.
100°
4.下面两个轴对称图形分别只画出了一半,请画
出它们的另一半(直线L为对称轴).
解:如图所示.
1.如图,已知点A、B直线MN同侧两点,点A1、A
关于直线MN对称.连接A1B交直线MN于点P,连
接AP.
(1)若A1B=5cm,则AP+BP的长为 .
5cm
A
B
P
A1
N
M
拓展提升
(2)某乡为了解决所辖范围内张家村A和李家村B的饮水问题,决定在河MN边打开一个缺口P将河水引入到张家村A和李家村B.为了节约资金,使修建的水渠最短,应将缺口P修建在哪里 请你利用所学知识解决这一问题,并用红色线段画出水渠.
A
B
P
M
N
A
B
M
A1
2.如图,已知点P是∠AOB内任意一点,点P1,P
关于OA对称,点P2,P关于OB对称.连接P1P2,分
别交OA,OB于C, D.连接PC,PD.若P1P2=10cm,
则△PCD的周长为 .
10cm
.
.
P2
P
.
P1
C
D
B
A
O
课堂小结
轴对称的性质
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
1.如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A. 1个 B. 2个 C. 3个 D. 4个
C
解析:△HEC关于CD对称;△FDB关于BE对称;△GED关于HF对称;关于AG对称的是它本身.所以共3个.故选C.
当堂检测
2.作△ABC关于直线l对称的△A′B′C′,点A,B,C的对称点分别是A′,B′,C′,则下列说法中正确的是( )
A. AA′垂直平分对称轴
B. △ABC和△A′B′C′的周长相等
C. 线段AB′被对称轴平分
D. △ABC的面积被对称轴平分
B
3.如图,∠A=30°,∠C′=60°,△ABC 与△A′B′C′关于直线l对称,则∠B= .
解析:∵△ABC 与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,∴∠C=∠C′=60°,
∵∠A=30°,∴∠B=180°-∠A-∠C=180°-30°-60°=90°.
故答案为:90°.
90°
5.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.
解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°
∴∠ABC=2∠C=60°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
