5.3 简单的轴对称图形(第1课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 5.3 简单的轴对称图形(第1课时)教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第五章 生活中的轴对称
第五章 生活中的轴对称
5.3简单的轴对称图形
(第1课时)
学 习 目 标
1
2
经历剪纸、折纸等 活动,进一步认识等腰三角形,了解等腰三角形是 轴对称图形. (重点)
能够探索、归纳、验证等腰三角形的性质,并学会应用等腰三角形的性质. (重、难点)
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
情景导入
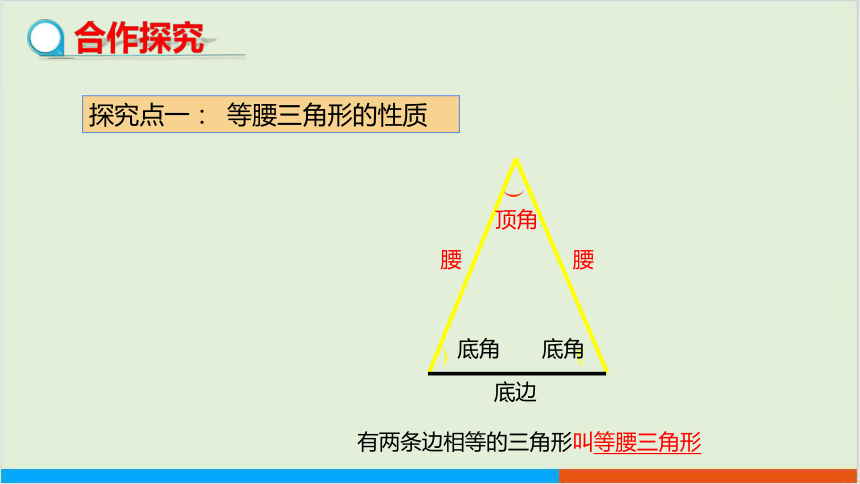
有两条边相等的三角形叫等腰三角形
(
(
顶角
底角
底角
腰
腰
底边
)
合作探究
探究点一: 等腰三角形的性质
生活中的等腰三角形
1.等腰三角形是轴对称图形吗?找出对称轴.
2.顶角的平分线所在的直线是等腰三角形的对称轴吗?
3.底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由.
思考
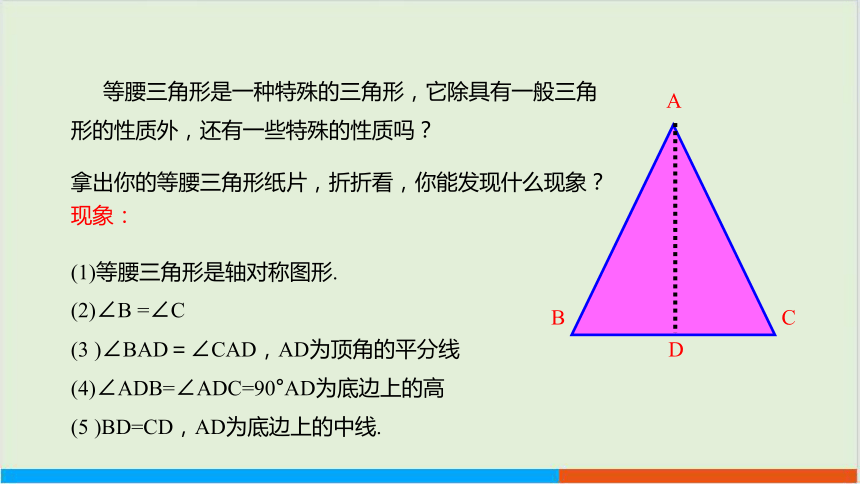
(1)等腰三角形是轴对称图形.
(2)∠B =∠C
(3 )∠BAD=∠CAD,AD为顶角的平分线
(4)∠ADB=∠ADC=90°AD为底边上的高
(5 )BD=CD,AD为底边上的中线.
A
B
C
D
现象:
等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊的性质吗?
拿出你的等腰三角形纸片,折折看,你能发现什么现象?
A
B
C
D
现象(3)、(4)、(5)能用一句话归纳出来吗?
现象(2)能用一句话归纳出来吗?
等腰三角形的两个底角相等
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)
归纳
A
B
C
D
在ΔABC中∵ AD是角平分线,
∴∠BAD=∠CAD.
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD
∴BD=CD, ∠ADB=∠ADC=90
∴AD是ΔABC的角平分线、底边上的中线、底边上的高.
三线合一吗?
证明
等腰三角形的性质
1.等腰三角形是轴对称图形.
3.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
知识讲解
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
合作探究
探究点一: 等边三角形的性质
等边三角形的性质:
1.等边三角形是轴对称图形.
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴.
等边三角形共有三条对称轴.
3.等边三角形的各角都相等,都等于60°
知识讲解
例1 .如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, 求:△ABC各角的度数.
解:因为AB=AC,BD=BC=AD,
所以∠ABC=∠C=∠BDC.
∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°.
在△ABC中,∠A=35°,∠ABC=∠C=72°
例题讲解
三条边相等
1、等边对等角
(等腰三角形的两底角相等)
2、三线合一(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
1、每个内角都等于60o
2、三组“三线合一”
(每个角的平分线都与它对边上的中线及高互相重合)
课堂小结
等腰三角形
等边三角形
1、等腰三角形的顶角是36度,则底角是_____________.
2、若等腰三角形的两边长分别是3m和6cm ,则其周长是____________.
3.下列命题中:(1)等腰三角形的两角相等;(2)等腰三角形的顶角平分线必平分底边;(3)等腰三角形一边上的中线也是这边上的高线; (4) 等腰三角形底边上的高线平分顶角.其中正确的有( )
A. (1)(3) B. (2)(4)
C. (1)(2)(4) D. (2)(3)(4)
15
B
72°
当堂检测
4. 如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC.
解:(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°.
第五章 生活中的轴对称
第五章 生活中的轴对称
5.3简单的轴对称图形
(第1课时)
学 习 目 标
1
2
经历剪纸、折纸等 活动,进一步认识等腰三角形,了解等腰三角形是 轴对称图形. (重点)
能够探索、归纳、验证等腰三角形的性质,并学会应用等腰三角形的性质. (重、难点)
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
情景导入
有两条边相等的三角形叫等腰三角形
(
(
顶角
底角
底角
腰
腰
底边
)
合作探究
探究点一: 等腰三角形的性质
生活中的等腰三角形
1.等腰三角形是轴对称图形吗?找出对称轴.
2.顶角的平分线所在的直线是等腰三角形的对称轴吗?
3.底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在直线呢?
4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由.
思考
(1)等腰三角形是轴对称图形.
(2)∠B =∠C
(3 )∠BAD=∠CAD,AD为顶角的平分线
(4)∠ADB=∠ADC=90°AD为底边上的高
(5 )BD=CD,AD为底边上的中线.
A
B
C
D
现象:
等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊的性质吗?
拿出你的等腰三角形纸片,折折看,你能发现什么现象?
A
B
C
D
现象(3)、(4)、(5)能用一句话归纳出来吗?
现象(2)能用一句话归纳出来吗?
等腰三角形的两个底角相等
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)
归纳
A
B
C
D
在ΔABC中∵ AD是角平分线,
∴∠BAD=∠CAD.
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD
∴BD=CD, ∠ADB=∠ADC=90
∴AD是ΔABC的角平分线、底边上的中线、底边上的高.
三线合一吗?
证明
等腰三角形的性质
1.等腰三角形是轴对称图形.
3.等腰三角形的两个底角相等.
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
知识讲解
三边都相等的三角形是等边三角形也叫正三角形
(1)等边三角形是轴对称图形吗?找出对称轴
(2)你能发现它的哪些特征?
合作探究
探究点一: 等边三角形的性质
等边三角形的性质:
1.等边三角形是轴对称图形.
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴.
等边三角形共有三条对称轴.
3.等边三角形的各角都相等,都等于60°
知识讲解
例1 .如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD, 求:△ABC各角的度数.
解:因为AB=AC,BD=BC=AD,
所以∠ABC=∠C=∠BDC.
∠A=∠ABD(等边对等角).
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°.
在△ABC中,∠A=35°,∠ABC=∠C=72°
例题讲解
三条边相等
1、等边对等角
(等腰三角形的两底角相等)
2、三线合一(等腰三角形顶角平分线、底边上的中线、底边上的高互相重合)
1、每个内角都等于60o
2、三组“三线合一”
(每个角的平分线都与它对边上的中线及高互相重合)
课堂小结
等腰三角形
等边三角形
1、等腰三角形的顶角是36度,则底角是_____________.
2、若等腰三角形的两边长分别是3m和6cm ,则其周长是____________.
3.下列命题中:(1)等腰三角形的两角相等;(2)等腰三角形的顶角平分线必平分底边;(3)等腰三角形一边上的中线也是这边上的高线; (4) 等腰三角形底边上的高线平分顶角.其中正确的有( )
A. (1)(3) B. (2)(4)
C. (1)(2)(4) D. (2)(3)(4)
15
B
72°
当堂检测
4. 如图,在等腰△ABC中,∠A=80°,∠B和∠C的平分线相交于点O
(1)连接OA,求∠OAC的度数;
(2)求:∠BOC.
解:(1)连接AO,
∵在等腰△ABC中,∠B和∠C的平分线相交于点O,
∴等腰△ABC关于线段AO所在的直线对称,
∵∠A=80°,
∴∠OAC=40°
(2)∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC= ∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-( ∠ABC+∠ACB)
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+∠A。
∴当∠A=80°时,
∠BOC=180° (∠B+∠C)=90°+∠A=130°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
