1.2 幂的乘方与积的乘方(第2课时)教学课件 北师大版中学数学七年级(下)
文档属性
| 名称 | 1.2 幂的乘方与积的乘方(第2课时)教学课件 北师大版中学数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第 一 章 整式的乘除
第一章 整式的乘除
1.2 幂的乘方与积的乘方
第2课时 积的乘方
学 习 目 标
1.经历探索积的乘方运算性质的过程,理解并掌握积的乘方法则.(重点)
2.会运用积的乘方的运算性质进行运算.(难点)
想一想:
新课导入
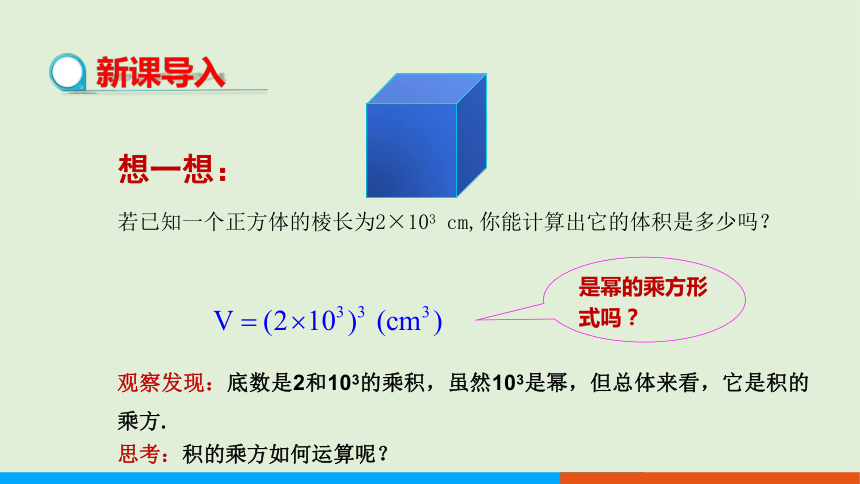
若已知一个正方体的棱长为2×103 cm,你能计算出它的体积是多少吗?
观察发现:底数是2和103的乘积,虽然103是幂,但总体来看,它是积的乘方.
是幂的乘方形式吗?
思考:积的乘方如何运算呢?
1.剪一剪,想一想
a
2a
a
2a
2.切一切,议一议
探究活动
(2a)2=4a2
(2a) 3=8a3
知识讲解
问题:填空,看看运算过程用到哪些运算律,从运算结果看能发现什么规律?
猜想:积的乘方(ab)n = anbn (n为正整数)
(1)()2=()·()=(·)·(·)
=( )( )
(2)()3=_______________
=___________
=( )( )
2
2
()·( )·( )
()·()
3
3
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
推导过程
个
个
个
语言表述:
积的乘方的运算性质
积的乘方,等于把积中的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
想一想:三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
积的乘方的运算性质的逆用
anbn = (ab)n (n为正整数)
计算:
例1
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
.
=-125b3.
=x2y4.
=16x12.
(-5)3·b3
x2·(y2)2
(-2)4·(x3)4
注意:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
例2
计算:
(1) 3 · 4· +(2)4+(-2 4)2
(2) 2(3)2 · 3-(3 3)3+(5 )2 · 7
解: (1)原式= 3+4+1+ 2×4+(-2)2 · (4)2
(2)原式=2 6 · 3-27 9+25 2 · 7
注意:运算顺序是先乘方,再乘除,最后算加减。
= 8+ 8+4 8
=6 8
=2 9-27 9+25 9
=0
例3
计算:(0.04)100×[(-5)100]2
=(0.22)100 × 5200
=(0.2)200 × 5200
=(0.2×5)200
=1200
(0.04)100×[(-5)100]2
=1.
解法一:
=(0.04)100× [(-5)2]100
=(0.04×25)100
=1100
=1.
= (0.04)100 ×(25)100
(0.04)100×[(-5)100]2
解法二:
随堂训练
1.
下列各式中正确的有几个?( )
A.1个 B.2个 C.3个 D.4个
A
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) -(-ab2)2=a2b4 ( )
2.判断:
√
( )
)
)
7
(
)
5
(
-
-
1
7
3
3
7
(
)
7
3
(
3
5
5
5
=
-
=
(
-
×
计算:
(1)(-223)3
(2) (-332)4
3.
解:(1)原式=(-2)3 ·(2)3 ·(3)3
(2)原式=(-3)4 ·(3)4 ·(2)4 · 4
=-869
= 81 1284
4.如果(an·bm·b)3=a9b15,求m,n的值.
(an)3·(bm)3·b3=a9b15,
a3n ·b3m·b3=a9b15 ,
a3n ·b3m+3=a9b15,
3n=9 ,3m+3=15,
n=3,m=4.
解:∵(an·bm·b)3=a9b15,
已知=5,=3,求(-)的值.
练一练:
课堂小结
1、积的乘方的运算性质
语言表述:
积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
(abc)n = anbncn (n为正整数)
2.积的乘方运算性质的推广
3.积的乘方运算性质的逆用
anbn = (ab)n (n为正整数)
第 一 章 整式的乘除
第一章 整式的乘除
1.2 幂的乘方与积的乘方
第2课时 积的乘方
学 习 目 标
1.经历探索积的乘方运算性质的过程,理解并掌握积的乘方法则.(重点)
2.会运用积的乘方的运算性质进行运算.(难点)
想一想:
新课导入
若已知一个正方体的棱长为2×103 cm,你能计算出它的体积是多少吗?
观察发现:底数是2和103的乘积,虽然103是幂,但总体来看,它是积的乘方.
是幂的乘方形式吗?
思考:积的乘方如何运算呢?
1.剪一剪,想一想
a
2a
a
2a
2.切一切,议一议
探究活动
(2a)2=4a2
(2a) 3=8a3
知识讲解
问题:填空,看看运算过程用到哪些运算律,从运算结果看能发现什么规律?
猜想:积的乘方(ab)n = anbn (n为正整数)
(1)()2=()·()=(·)·(·)
=( )( )
(2)()3=_______________
=___________
=( )( )
2
2
()·( )·( )
()·()
3
3
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
推导过程
个
个
个
语言表述:
积的乘方的运算性质
积的乘方,等于把积中的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
想一想:三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
积的乘方的运算性质的逆用
anbn = (ab)n (n为正整数)
计算:
例1
(1) (2a)3 ; (2) (-5b)3 ;
(3) (xy2)2 ; (4) (-2x3)4.
解:(1)原式=
(2)原式=
(3)原式=
(4)原式=
.
=-125b3.
=x2y4.
=16x12.
(-5)3·b3
x2·(y2)2
(-2)4·(x3)4
注意:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
例2
计算:
(1) 3 · 4· +(2)4+(-2 4)2
(2) 2(3)2 · 3-(3 3)3+(5 )2 · 7
解: (1)原式= 3+4+1+ 2×4+(-2)2 · (4)2
(2)原式=2 6 · 3-27 9+25 2 · 7
注意:运算顺序是先乘方,再乘除,最后算加减。
= 8+ 8+4 8
=6 8
=2 9-27 9+25 9
=0
例3
计算:(0.04)100×[(-5)100]2
=(0.22)100 × 5200
=(0.2)200 × 5200
=(0.2×5)200
=1200
(0.04)100×[(-5)100]2
=1.
解法一:
=(0.04)100× [(-5)2]100
=(0.04×25)100
=1100
=1.
= (0.04)100 ×(25)100
(0.04)100×[(-5)100]2
解法二:
随堂训练
1.
下列各式中正确的有几个?( )
A.1个 B.2个 C.3个 D.4个
A
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) -(-ab2)2=a2b4 ( )
2.判断:
√
( )
)
)
7
(
)
5
(
-
-
1
7
3
3
7
(
)
7
3
(
3
5
5
5
=
-
=
(
-
×
计算:
(1)(-223)3
(2) (-332)4
3.
解:(1)原式=(-2)3 ·(2)3 ·(3)3
(2)原式=(-3)4 ·(3)4 ·(2)4 · 4
=-869
= 81 1284
4.如果(an·bm·b)3=a9b15,求m,n的值.
(an)3·(bm)3·b3=a9b15,
a3n ·b3m·b3=a9b15 ,
a3n ·b3m+3=a9b15,
3n=9 ,3m+3=15,
n=3,m=4.
解:∵(an·bm·b)3=a9b15,
已知=5,=3,求(-)的值.
练一练:
课堂小结
1、积的乘方的运算性质
语言表述:
积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
(abc)n = anbncn (n为正整数)
2.积的乘方运算性质的推广
3.积的乘方运算性质的逆用
anbn = (ab)n (n为正整数)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
