6.4多边形的内角和与外角和(第1课时)教学详案--北师大版初中数学八年级(下)
文档属性
| 名称 | 6.4多边形的内角和与外角和(第1课时)教学详案--北师大版初中数学八年级(下) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:11 | ||
图片预览

文档简介
6.4 多边形的内角和与外角和(第1课时 多边形的内角和)
教学目标
1.理解并掌握多边形的内角和定理,且能够证明它.
2.能够应用多边形的内角和定理解决有关的问题.
3.经历多边形的内角和定理的探究过程,进一步体会转化的数学思想.
教学重点难点
重点:应用多边形内角和解决有关的问题.
难点:多边形的内角和公式的推导.
教学过程
知识回顾
【问题】(学生自主完成,老师引导)
1.△ABC中,∠A=50°,∠B=30°,则∠C=_____.
2.正方形的内角和等于多少度?长方形呢?
3.如图,对于任意形状的四边形它的内角和是多少度呢?你是怎么得到的?
探究新知
【问题】(激发学习兴趣) 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
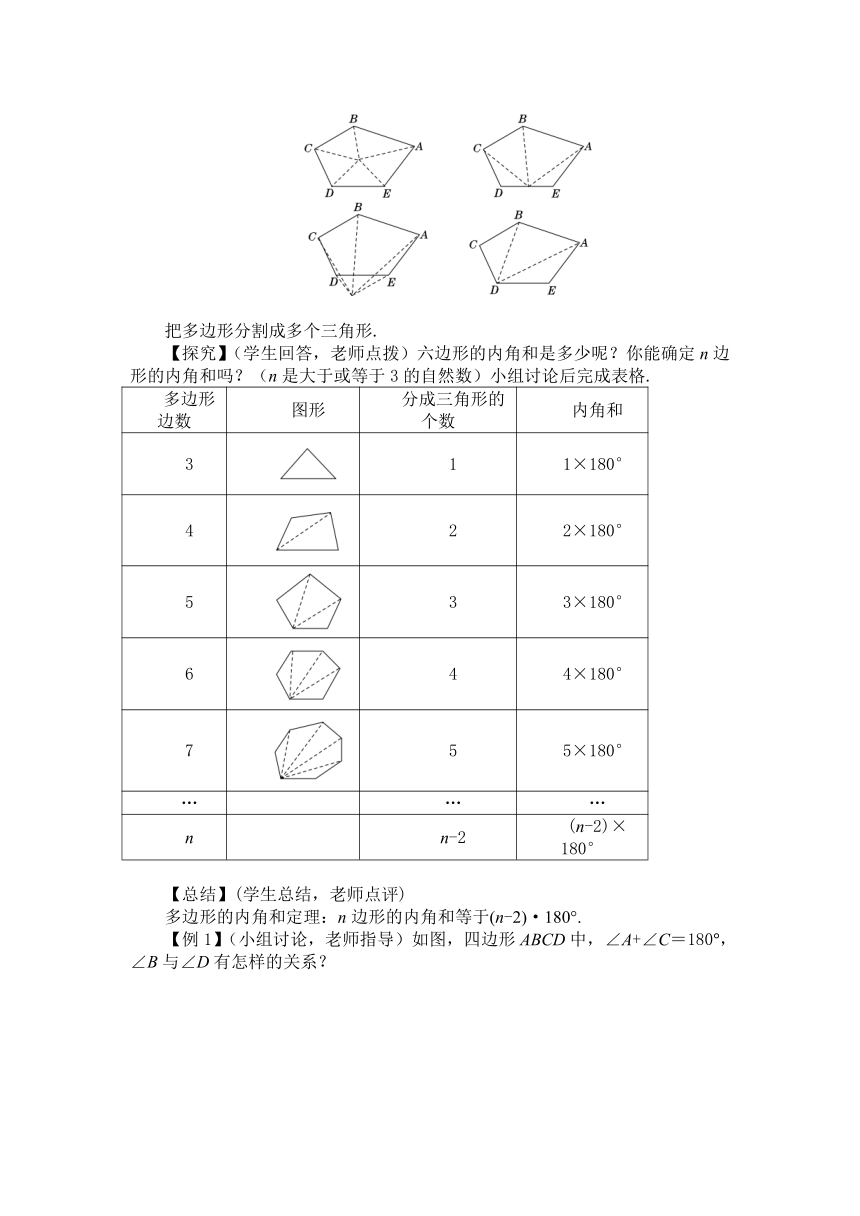
【探究】(小组讨论,老师点拨)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
把多边形分割成多个三角形.
【探究】(学生回答,老师点拨)六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
多边形边数 图形 分成三角形的个数 内角和
3 1 1×180°
4 2 2×180°
5 3 3×180°
6 4 4×180°
7 5 5×180°
… … …
n n-2 (n-2)×180°
【总结】(学生总结,老师点评)
多边形的内角和定理:n边形的内角和等于(n-2)·180°.
【例1】(小组讨论,老师指导)如图,四边形ABCD中,∠A+∠C=180,∠B与∠D有怎样的关系?
∠B+∠D=180.
结论:如果四边形的一组对角互补,那么另一组对角也互补.
【例2】(合作探究,解决问题)一个多边形的内角和为1 440,则它是几边形?
解:设这个多边形是n边形,则180·(n-2)=1 440,
∴ n=10,
∴这个多边形是十边形.
【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解.
【练习】(学生独立完成)1.六边形的内角和为( )
A.1 260° B.1 080°
C.900° D.720°
2.八边形的七个内角都为150,则第八个内角=________.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
答案:
1.D 2.30° 3.七边形 900°
【探究】(小组讨论)1.正三角形(等边三角形)的每个内角等于多少度?你是怎么计算的?
2.正四边形(正方形)的每个内角等于多少度?你是怎么计算的?
3.正五边形、正六边形、正八边形呢?…正n边形呢?
正n边形的每个内角度数为:.
【练习】一个多边形的每个内角均为120,则这个多边形是( )
A.正四边形 B.正五边形 C.正六边形 D正.七边形
答案:C
【拓展】(学生动手实践)截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
不过顶点 五边形 过一顶点 四边形 过两顶点 三角形
【总结】截一个多边形的一个角时,一定注意截法,注意分类讨论.
课堂练习
1.一个多边形的内角和为540°,则它是( )
A.四边形 B.五边形
C.六边形 D.七边形
2.一个多边形的内角和为1 800°, 截去一个角后, 得到的多边形的内角和 为( )
A.1 620° B.1 800°
C.1 980° D.以上答案都有可能
3.多边形每一个内角都等于150°,则该多边形的边数是( )
A.10 B.11
C.12 D.13
4.m边形与n边形内角和的差为720°,则m与n的差为( )
A.2 B.3
C.4 D.5
5.已知甲多边形的内角和是乙多边形内角和的2倍,而从甲多边形一个顶点出发所引对角线的条数与从乙多边形一个顶点出发所引对角线的条数的比是 7∶3,如果甲是十边形,那么乙是 边形.
6.一个同学在进行多边形的内角和计算时,求得内角和为1 125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
7.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在模板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,判断此模板是否合格?为什么?
参考答案
1.B 2.D 3.C 4.C 5.六
6. 解:设此多边形的内角和为x,则有
1 125<x<1 125+180,
即180×6+45<x<180×7+45.
∵x为多边形的内角和,∴x=180°×7=1 260.
∴7+2=9,1 260-1 125=135°.
∴少算的这个内角是135,这个多边形是九边形.
7.解:不合格,组成的五边形的内角和不是540°.
课堂小结
1.多边形的内角和定理:n边形的内角和等于(n - 2)·180°.
2.正n边形的每个内角度数为:.
布置作业
教材习题6.7题1、题2、题3.
板书设计
4 多边形的内角和与外角和
第1课时 多边形的内角和
1.多边形的内角和定理:n边形的内角和等于(n-2)·180°.
例1如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例2 一个多边形的内角和为1 440°,则它是几边形?
2.正n边形的每个内角度数为:.
拓展 截去一张长方形纸片的一个角后,纸片还剩几个角?
教学目标
1.理解并掌握多边形的内角和定理,且能够证明它.
2.能够应用多边形的内角和定理解决有关的问题.
3.经历多边形的内角和定理的探究过程,进一步体会转化的数学思想.
教学重点难点
重点:应用多边形内角和解决有关的问题.
难点:多边形的内角和公式的推导.
教学过程
知识回顾
【问题】(学生自主完成,老师引导)
1.△ABC中,∠A=50°,∠B=30°,则∠C=_____.
2.正方形的内角和等于多少度?长方形呢?
3.如图,对于任意形状的四边形它的内角和是多少度呢?你是怎么得到的?
探究新知
【问题】(激发学习兴趣) 某小区健身广场中心的边缘是一个五边形(如图),你能求出它的五个内角的和吗?
【探究】(小组讨论,老师点拨)小明、小亮分别利用下面的图形求出了五边形的五个内角的和.你知道他们是怎样做的吗?
把多边形分割成多个三角形.
【探究】(学生回答,老师点拨)六边形的内角和是多少呢?你能确定n边形的内角和吗?(n是大于或等于3的自然数)小组讨论后完成表格.
多边形边数 图形 分成三角形的个数 内角和
3 1 1×180°
4 2 2×180°
5 3 3×180°
6 4 4×180°
7 5 5×180°
… … …
n n-2 (n-2)×180°
【总结】(学生总结,老师点评)
多边形的内角和定理:n边形的内角和等于(n-2)·180°.
【例1】(小组讨论,老师指导)如图,四边形ABCD中,∠A+∠C=180,∠B与∠D有怎样的关系?
∠B+∠D=180.
结论:如果四边形的一组对角互补,那么另一组对角也互补.
【例2】(合作探究,解决问题)一个多边形的内角和为1 440,则它是几边形?
解:设这个多边形是n边形,则180·(n-2)=1 440,
∴ n=10,
∴这个多边形是十边形.
【总结】已知多边形内角和求边数时,一般是设出多边形的边数,根据多边形内角和公式列方程求解.
【练习】(学生独立完成)1.六边形的内角和为( )
A.1 260° B.1 080°
C.900° D.720°
2.八边形的七个内角都为150,则第八个内角=________.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
答案:
1.D 2.30° 3.七边形 900°
【探究】(小组讨论)1.正三角形(等边三角形)的每个内角等于多少度?你是怎么计算的?
2.正四边形(正方形)的每个内角等于多少度?你是怎么计算的?
3.正五边形、正六边形、正八边形呢?…正n边形呢?
正n边形的每个内角度数为:.
【练习】一个多边形的每个内角均为120,则这个多边形是( )
A.正四边形 B.正五边形 C.正六边形 D正.七边形
答案:C
【拓展】(学生动手实践)截去一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.
不过顶点 五边形 过一顶点 四边形 过两顶点 三角形
【总结】截一个多边形的一个角时,一定注意截法,注意分类讨论.
课堂练习
1.一个多边形的内角和为540°,则它是( )
A.四边形 B.五边形
C.六边形 D.七边形
2.一个多边形的内角和为1 800°, 截去一个角后, 得到的多边形的内角和 为( )
A.1 620° B.1 800°
C.1 980° D.以上答案都有可能
3.多边形每一个内角都等于150°,则该多边形的边数是( )
A.10 B.11
C.12 D.13
4.m边形与n边形内角和的差为720°,则m与n的差为( )
A.2 B.3
C.4 D.5
5.已知甲多边形的内角和是乙多边形内角和的2倍,而从甲多边形一个顶点出发所引对角线的条数与从乙多边形一个顶点出发所引对角线的条数的比是 7∶3,如果甲是十边形,那么乙是 边形.
6.一个同学在进行多边形的内角和计算时,求得内角和为1 125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
7.如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在模板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,判断此模板是否合格?为什么?
参考答案
1.B 2.D 3.C 4.C 5.六
6. 解:设此多边形的内角和为x,则有
1 125<x<1 125+180,
即180×6+45<x<180×7+45.
∵x为多边形的内角和,∴x=180°×7=1 260.
∴7+2=9,1 260-1 125=135°.
∴少算的这个内角是135,这个多边形是九边形.
7.解:不合格,组成的五边形的内角和不是540°.
课堂小结
1.多边形的内角和定理:n边形的内角和等于(n - 2)·180°.
2.正n边形的每个内角度数为:.
布置作业
教材习题6.7题1、题2、题3.
板书设计
4 多边形的内角和与外角和
第1课时 多边形的内角和
1.多边形的内角和定理:n边形的内角和等于(n-2)·180°.
例1如图,四边形ABCD中,∠A+∠C=180°,∠B与∠D有怎样的关系?
例2 一个多边形的内角和为1 440°,则它是几边形?
2.正n边形的每个内角度数为:.
拓展 截去一张长方形纸片的一个角后,纸片还剩几个角?
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
