第6章6.2实数(第1课时 实数的概念及分类) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第6章6.2实数(第1课时 实数的概念及分类) 教学课件--沪科版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第6章 实 数
6.2 实 数
第1课时 实数的概念及分类
学 习 目 标
1
2
会用无限逼近的思想,探索无理数是无限不循环小数.
掌握无理数、实数的概念,能判断一个数是否为无理数.(重点)
初步掌握实数的分类.(难点)
3
知识回顾
什么叫做有理数 有理数如何分类
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , ,5.2, …
负分数:如 , ,-3.5, …
有理数
除了有理数外还有没有其他的数呢?
新课导入
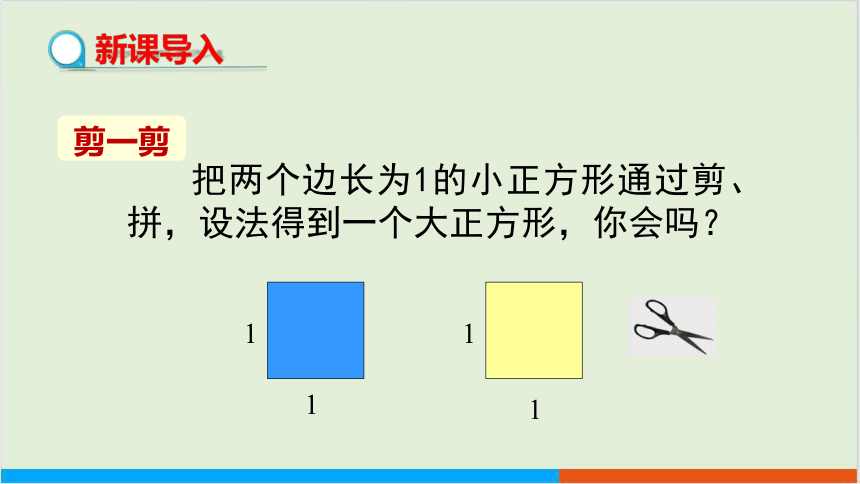
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
1
剪一剪
新课导入
1
1
1
1
1
1
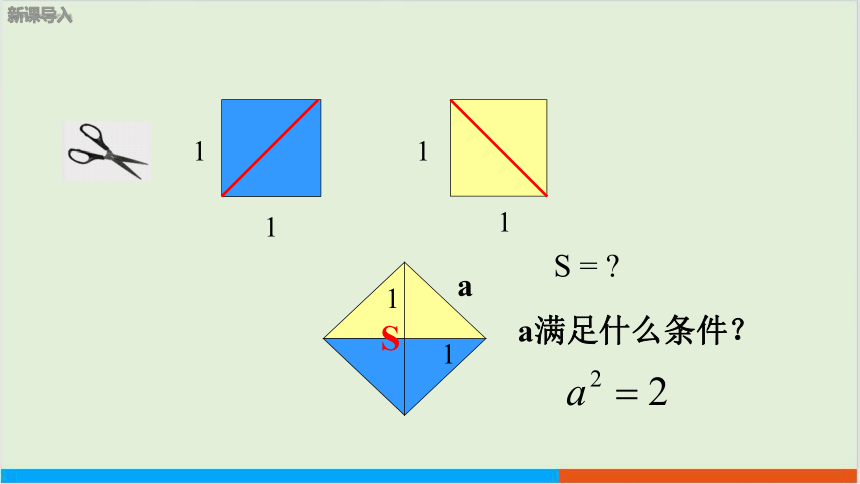
a
S =
a满足什么条件?
S
新课导入
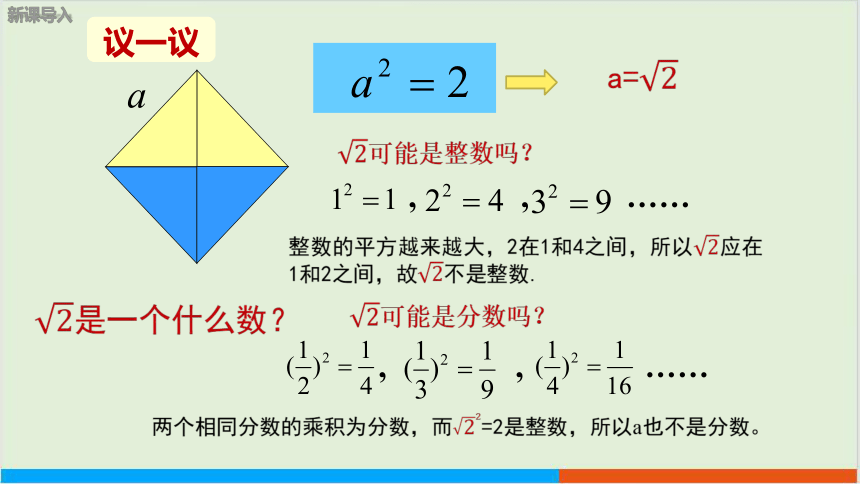
可能是整数吗?
, , ……
整数的平方越来越大,2在1和4之间,所以应在1和2之间,故不是整数.
可能是分数吗?
, , ……
两个相同分数的乘积为分数,而=2是整数,所以a也不是分数。
a=
议一议
?
知识讲解
探究
因为 12=1,22=4,而 1 < 2 < 4,
所以.
如何得到 的更精确的范围?
知识讲解
如此下去,可以得到的更精确的近似值.
∵,
∴<1.5.
∵
∵,
∴<1.42.
∴<1.415.
……
知识讲解
继续重复上述的过程,可以得到
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
是一个无限不循环的小数.
知识讲解
我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
思考
知识讲解
思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?
可以
(2)由此你可以得到什么结论?
任何一个有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数或无限循环小数也都是有理数.
思考2:除了有限小数和无限循环小数,还有什么其他类
型的小数吗?
无限不循环小数,比如
知识讲解
2.02002000200002
它们都是无限不循环小数
常见的一些无限不循环小数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
=1.73205080
知识讲解
无限不循环小数叫做无理数.
定义
无理数可分为正无理数与负无理数,如 , ,π是正无理数;- ,- ,-π是负无理数.
有理数和无理数统称为实数.
知识讲解
有理数集合
无理数集合
...
...
练一练
把下列各数分别填入相应的集合内:
知识讲解
我们认识的数的范围又一次扩大了,我们可以将实数按如下方式分类:
按定义分
知识讲解
判断:
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
×
×
×
随堂训练
2.下列面积的正方形,边长不是有理数的是 ( )
A. 16 B. 25 C. 2 D. 4
C
1.估计位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
随堂训练
3.判断正误
(1)不带根号的数都是有理数( )
(2)带根号的数都是无理数( )
(3)无理数都是无限小数( )
(4)无限小数都是无理数( )
×
×
×
随堂训练
4、下列各数中,哪些是有理数?哪些是无理数?
0.351,- ,3.14159,-5.2323332…,
123456789101112…(由连续的正整数组成).
解:有理数有0.351,- , ,3.14159
无理数有-5.2323332…,123456789101112….
课堂小结
无限不循环小数叫做无理数;有理数与无理数统称实数.
1. 无理数及实数的概念
2. 实数的分类
第6章 实 数
6.2 实 数
第1课时 实数的概念及分类
学 习 目 标
1
2
会用无限逼近的思想,探索无理数是无限不循环小数.
掌握无理数、实数的概念,能判断一个数是否为无理数.(重点)
初步掌握实数的分类.(难点)
3
知识回顾
什么叫做有理数 有理数如何分类
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , ,5.2, …
负分数:如 , ,-3.5, …
有理数
除了有理数外还有没有其他的数呢?
新课导入
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
1
剪一剪
新课导入
1
1
1
1
1
1
a
S =
a满足什么条件?
S
新课导入
可能是整数吗?
, , ……
整数的平方越来越大,2在1和4之间,所以应在1和2之间,故不是整数.
可能是分数吗?
, , ……
两个相同分数的乘积为分数,而=2是整数,所以a也不是分数。
a=
议一议
?
知识讲解
探究
因为 12=1,22=4,而 1 < 2 < 4,
所以.
如何得到 的更精确的范围?
知识讲解
如此下去,可以得到的更精确的近似值.
∵,
∴<1.5.
∵
∵,
∴<1.42.
∴<1.415.
……
知识讲解
继续重复上述的过程,可以得到
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
是一个无限不循环的小数.
知识讲解
我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
思考
知识讲解
思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?
可以
(2)由此你可以得到什么结论?
任何一个有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数或无限循环小数也都是有理数.
思考2:除了有限小数和无限循环小数,还有什么其他类
型的小数吗?
无限不循环小数,比如
知识讲解
2.02002000200002
它们都是无限不循环小数
常见的一些无限不循环小数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
=1.73205080
知识讲解
无限不循环小数叫做无理数.
定义
无理数可分为正无理数与负无理数,如 , ,π是正无理数;- ,- ,-π是负无理数.
有理数和无理数统称为实数.
知识讲解
有理数集合
无理数集合
...
...
练一练
把下列各数分别填入相应的集合内:
知识讲解
我们认识的数的范围又一次扩大了,我们可以将实数按如下方式分类:
按定义分
知识讲解
判断:
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
×
×
×
随堂训练
2.下列面积的正方形,边长不是有理数的是 ( )
A. 16 B. 25 C. 2 D. 4
C
1.估计位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
随堂训练
3.判断正误
(1)不带根号的数都是有理数( )
(2)带根号的数都是无理数( )
(3)无理数都是无限小数( )
(4)无限小数都是无理数( )
×
×
×
随堂训练
4、下列各数中,哪些是有理数?哪些是无理数?
0.351,- ,3.14159,-5.2323332…,
123456789101112…(由连续的正整数组成).
解:有理数有0.351,- , ,3.14159
无理数有-5.2323332…,123456789101112….
课堂小结
无限不循环小数叫做无理数;有理数与无理数统称实数.
1. 无理数及实数的概念
2. 实数的分类
