第8章8.2整式乘法(第2课时 单项式与多项式相乘) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第8章8.2整式乘法(第2课时 单项式与多项式相乘) 教学课件--沪科版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:20 | ||
图片预览








文档简介
(共24张PPT)
第8章 整式乘除与因式分解
第2课时 单项式与多项式相乘
8.2 整式乘法
学 习 目 标
1.能根据乘法分配律和单项式与单项式相乘的法则,
探究单项式与多项式相乘的法则,掌握单项式与多项式相乘的法则并会运用. (重、难点)
2. 掌握多项式除以单项式法则,能熟练进行多项式除以单项式的运算. (重点)
知识回顾
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数
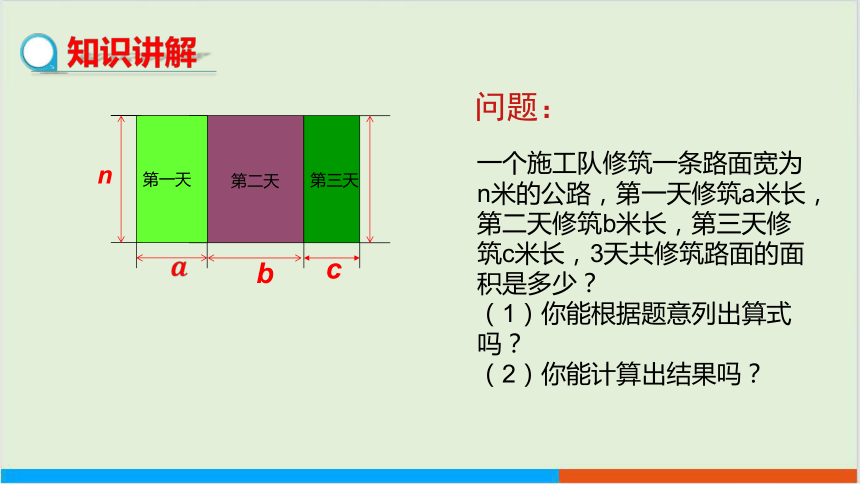
一个施工队修筑一条路面宽为n米的公路,第一天修筑a米长,第二天修筑b米长,第三天修筑c米长,3天共修筑路面的面积是多少?
(1)你能根据题意列出算式吗?
(2)你能计算出结果吗?
m
b
n
c
问题:
知识讲解
第一天
第二天
第三天
m
b
n
n
c
方法一:把3天修建的路面看成是长为 ,宽为n的矩形,其面积
方法二:把3天修建的路面看成是长分别为a、b、c,宽都是n的三个矩形的面积之和
问题:
乘法分配律:
第一天
第二天
第三天
n
b
n
c
n
第二天
第三天
第一天
如何计算:(-42)·(3+2)
思考:
(利用乘法的分配律转化为单项式乘单项式)
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,并把所得的积相加。
用字母表示如下:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
一、单项式与多项式的乘法法则
例1
计算:
(1)2ab(5ab2+3a2b);
(2)( -2ab)·
(3)5m2n(2n+3m-n2);
解:(1)原式=2ab·5ab2+2ab·3a2b
(2)原式=
(3)原式=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4)原式=(2x+2y2z+2xy2z3)·xyz
(4)2(x+y2z+xy2z3)·xyz.
=2x2yz+2xy3z2+2x2y3z4.
(2)单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定,多项式中的每一项前面的符号是性质符号,同号相乘得正,异号相乘得负,最后写成省略加号的代数和的形式;
【归纳】
解题时需要注意的问题:
(1)单项式乘多项式的积仍是多项式,其项数与原多项式的项数相同,不要出现漏乘现象;
(3)混合运算中,要注意运算顺序,结果有同类项的要合并同类项.
练一练
计算:
化简求值:-22·(2)-5(2),
其中=1,=-1.
解:原式=-2-22-5+
=-2-2-5+
=-7+3.
当=1,=-1 时,
原式=-7×13×(-1)+3×12×(-1)2
=-7×1×(-1)+3×1×1
=7+3=10.
例2
问题 如何计算(pa+pb+pc) ÷p
方法1:因为p(a+b+c )=pa+pb+pc,
所以 (pa+pb+pc) ÷p=a+b+c;
方法2:类比有理数的除法
(pa+pb+pc) ÷p=(pa+pb+pc)
=a+b+c.
多项式除以单项式
商式中的项a、b、c是怎样得到的?你能总结出多项式除以单项式的法则吗?
多项式除以单项式,先把这个多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
应用法则是把多项式除以单项式转化为单项式除以单项式.
二、多项式除以单项式的法则
例3
计算:
随堂训练
1.下列计算错误的是( )
(A)5(22-)=103-5
(B)-3+ 4-=-
(C)2=8
(D)(--12) (-)2=+2
D
=(--12) ()
=-+1+2
2.判断
×
×
)=( )
( )
(-2) (-3)=-22-2( )
×
3.计算:(1) –12a5b3c÷(–4a2b)=
(2)(–5a2b)2÷5a3b2 =
(3)4(a+b)7 ÷ (a+b)3 =
(4)(–3ab2c)3÷(–3ab2c)2 =
3a3b2c
5a
8(a+b)4
–3ab2c
4.计算:
-22·(2)-5(-)
解:原式=-
=-
=-7.
5.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
6.如果(-3x)2(x2-2nx+2)的展开式中不含x3 项, 求n的值.
解: (-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
解:根据题意得
4x4(2x2+1)+3x-2
=8x6+4x4+3x-2,
则这个多项式为8x6+4x4+3x-2.
“被除式=商×除式+余式”
7.已知一个多项式除以4x4,所得的商是
2x2+1,余式是3x-2,请求出这个多项式.
8.先化简,后求值:[2x(x2y-xy2)+xy(xy
-x2)]÷x2y,其中x=2021,y=2020.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2021,y=2020时,
原式=x-y=2021-2020=1.
课堂小结
单项式乘多项式
实质上是转化为单项式×单项式
注意
整式的乘法
(1)计算时,要注意符号问题,多项式中每一项都
包括它前面的符号,单项式分别与多项式的每
一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
多项式除以单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,多项式的各项要包括它们前面的符号,要注意符号的变化;
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
第8章 整式乘除与因式分解
第2课时 单项式与多项式相乘
8.2 整式乘法
学 习 目 标
1.能根据乘法分配律和单项式与单项式相乘的法则,
探究单项式与多项式相乘的法则,掌握单项式与多项式相乘的法则并会运用. (重、难点)
2. 掌握多项式除以单项式法则,能熟练进行多项式除以单项式的运算. (重点)
知识回顾
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数
一个施工队修筑一条路面宽为n米的公路,第一天修筑a米长,第二天修筑b米长,第三天修筑c米长,3天共修筑路面的面积是多少?
(1)你能根据题意列出算式吗?
(2)你能计算出结果吗?
m
b
n
c
问题:
知识讲解
第一天
第二天
第三天
m
b
n
n
c
方法一:把3天修建的路面看成是长为 ,宽为n的矩形,其面积
方法二:把3天修建的路面看成是长分别为a、b、c,宽都是n的三个矩形的面积之和
问题:
乘法分配律:
第一天
第二天
第三天
n
b
n
c
n
第二天
第三天
第一天
如何计算:(-42)·(3+2)
思考:
(利用乘法的分配律转化为单项式乘单项式)
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,并把所得的积相加。
用字母表示如下:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
单项式与多项式的乘法法则
p(a+b+c)=pa+pb+pc
一、单项式与多项式的乘法法则
例1
计算:
(1)2ab(5ab2+3a2b);
(2)( -2ab)·
(3)5m2n(2n+3m-n2);
解:(1)原式=2ab·5ab2+2ab·3a2b
(2)原式=
(3)原式=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4)原式=(2x+2y2z+2xy2z3)·xyz
(4)2(x+y2z+xy2z3)·xyz.
=2x2yz+2xy3z2+2x2y3z4.
(2)单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定,多项式中的每一项前面的符号是性质符号,同号相乘得正,异号相乘得负,最后写成省略加号的代数和的形式;
【归纳】
解题时需要注意的问题:
(1)单项式乘多项式的积仍是多项式,其项数与原多项式的项数相同,不要出现漏乘现象;
(3)混合运算中,要注意运算顺序,结果有同类项的要合并同类项.
练一练
计算:
化简求值:-22·(2)-5(2),
其中=1,=-1.
解:原式=-2-22-5+
=-2-2-5+
=-7+3.
当=1,=-1 时,
原式=-7×13×(-1)+3×12×(-1)2
=-7×1×(-1)+3×1×1
=7+3=10.
例2
问题 如何计算(pa+pb+pc) ÷p
方法1:因为p(a+b+c )=pa+pb+pc,
所以 (pa+pb+pc) ÷p=a+b+c;
方法2:类比有理数的除法
(pa+pb+pc) ÷p=(pa+pb+pc)
=a+b+c.
多项式除以单项式
商式中的项a、b、c是怎样得到的?你能总结出多项式除以单项式的法则吗?
多项式除以单项式,先把这个多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
应用法则是把多项式除以单项式转化为单项式除以单项式.
二、多项式除以单项式的法则
例3
计算:
随堂训练
1.下列计算错误的是( )
(A)5(22-)=103-5
(B)-3+ 4-=-
(C)2=8
(D)(--12) (-)2=+2
D
=(--12) ()
=-+1+2
2.判断
×
×
)=( )
( )
(-2) (-3)=-22-2( )
×
3.计算:(1) –12a5b3c÷(–4a2b)=
(2)(–5a2b)2÷5a3b2 =
(3)4(a+b)7 ÷ (a+b)3 =
(4)(–3ab2c)3÷(–3ab2c)2 =
3a3b2c
5a
8(a+b)4
–3ab2c
4.计算:
-22·(2)-5(-)
解:原式=-
=-
=-7.
5.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,原式=-20×(-2)2+9×(-2)=-98.
6.如果(-3x)2(x2-2nx+2)的展开式中不含x3 项, 求n的值.
解: (-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
解:根据题意得
4x4(2x2+1)+3x-2
=8x6+4x4+3x-2,
则这个多项式为8x6+4x4+3x-2.
“被除式=商×除式+余式”
7.已知一个多项式除以4x4,所得的商是
2x2+1,余式是3x-2,请求出这个多项式.
8.先化简,后求值:[2x(x2y-xy2)+xy(xy
-x2)]÷x2y,其中x=2021,y=2020.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2021,y=2020时,
原式=x-y=2021-2020=1.
课堂小结
单项式乘多项式
实质上是转化为单项式×单项式
注意
整式的乘法
(1)计算时,要注意符号问题,多项式中每一项都
包括它前面的符号,单项式分别与多项式的每
一项相乘时,同号相乘得正,异号相乘得负
(2)不要出现漏乘现象
(3)运算要有顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
多项式除以单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,多项式的各项要包括它们前面的符号,要注意符号的变化;
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
