第8章8.2整式乘法(第3课时 多项式与多项式相乘) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第8章8.2整式乘法(第3课时 多项式与多项式相乘) 教学课件--沪科版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第8章 整式乘法与因式分解
第3课时 多项式与多项式相乘
8.2 整式乘法
学 习 目 标
1.理解和掌握多项式与多项式的乘法法则及其推导过程.(重点)
2.能熟练运用法则进行多项式与多项式的乘法计算.(难点)
知识回顾
1.单项式与单项式相乘
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式。
2.单项式与多项式相乘
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,并把所得的积相加.
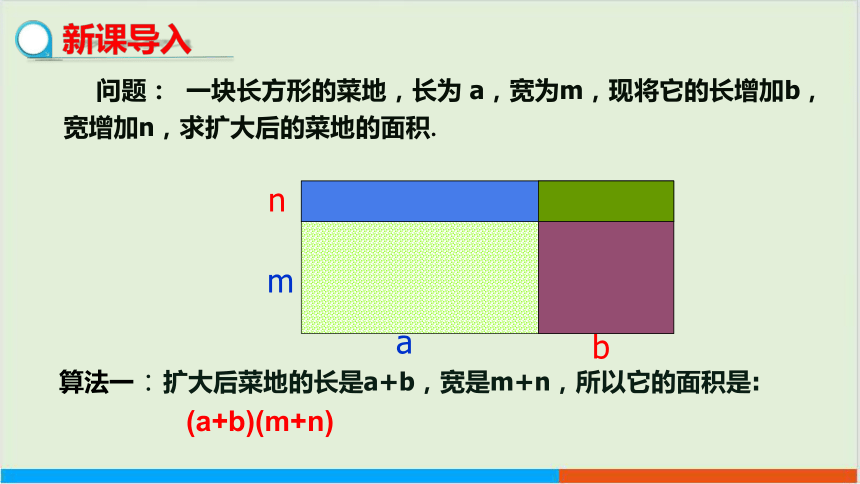
问题: 一块长方形的菜地,长为 a,宽为m,现将它的长增加b,宽增加n,求扩大后的菜地的面积.
n
b
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是:
(a+b)(m+n)
新课导入
问题 :一块长方形的菜地, 长为 a,宽为m,现将它的长增加b,宽增加n,求扩大后的菜地的面积.
m
a
am
n
an
b
bm
bn
am
an
bm
bn
+
+
+
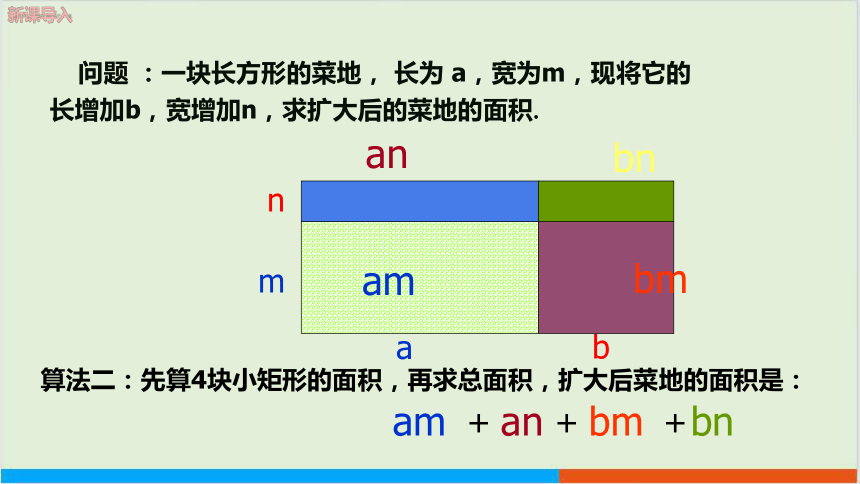
算法二:先算4块小矩形的面积,再求总面积,扩大后菜地的面积是:
(a+b)(m+n)
am+an+bm+bn
=
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
1
2
3
4
(a+b)(m+n)
am
1
2
3
4
+an
+bm
+bn
知识讲解
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项每一项相乘,再把所得的积相加.
①理解法则中两个“每一项”的含义,不要漏乘;
②多项式中每一项都包含它前面的符号,“同号得正,异号得负” ;
③展开式中有同类项的要合并同类项.
注意:
例1
(1) (+2)(5+3) ;
(2) (2 –3)(+4).
解:
(1)(+2 )(5 +3 )
=
=
(2)(2 –3)(+4)
2 2
+8
–3
–12
=2 2
+5
计算:
=
–12
·5
+
·3
+2
·5
+2
·3
5
+3
+10
+6
所得积的符号由这
两项的符号来确定:
负负得正
一正一负得负。
1. 两项相乘时,先定符号。
2.最后的结果要合并同类项.
先化简,再求值:
,其中
,
解:
例2
计算:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
拓展练习
随堂训练
1.下列多项式相乘,结果为x2-4x-12的是( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b
满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
B
C
3.计算:
(1)
(2)
(3)
(4)
解:原式
解:原式
解:原式
解:原式
解:原式
解:原式
4.化简求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中 x=1,y=-2.
解:(4x+3y)(4x-3y)+(2x+y)(3x-5y)
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
5.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a,b的值.
解: (ax2+bx+1)(3x-2)
=3ax3-2ax2+3bx2-2bx+3x-2
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
课堂小结
实质:转化为单项式乘多项式的运算
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项每一项相乘,再把所得的积相加.
(a+b)(m+n)
am+an+bm+bn
=
第8章 整式乘法与因式分解
第3课时 多项式与多项式相乘
8.2 整式乘法
学 习 目 标
1.理解和掌握多项式与多项式的乘法法则及其推导过程.(重点)
2.能熟练运用法则进行多项式与多项式的乘法计算.(难点)
知识回顾
1.单项式与单项式相乘
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式中含有的字母,则连同它的指数作为积的一个因式。
2.单项式与多项式相乘
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,并把所得的积相加.
问题: 一块长方形的菜地,长为 a,宽为m,现将它的长增加b,宽增加n,求扩大后的菜地的面积.
n
b
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是:
(a+b)(m+n)
新课导入
问题 :一块长方形的菜地, 长为 a,宽为m,现将它的长增加b,宽增加n,求扩大后的菜地的面积.
m
a
am
n
an
b
bm
bn
am
an
bm
bn
+
+
+
算法二:先算4块小矩形的面积,再求总面积,扩大后菜地的面积是:
(a+b)(m+n)
am+an+bm+bn
=
因为它们表示的都是同一块绿地的面积,所以可以得到结论:
1
2
3
4
(a+b)(m+n)
am
1
2
3
4
+an
+bm
+bn
知识讲解
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项每一项相乘,再把所得的积相加.
①理解法则中两个“每一项”的含义,不要漏乘;
②多项式中每一项都包含它前面的符号,“同号得正,异号得负” ;
③展开式中有同类项的要合并同类项.
注意:
例1
(1) (+2)(5+3) ;
(2) (2 –3)(+4).
解:
(1)(+2 )(5 +3 )
=
=
(2)(2 –3)(+4)
2 2
+8
–3
–12
=2 2
+5
计算:
=
–12
·5
+
·3
+2
·5
+2
·3
5
+3
+10
+6
所得积的符号由这
两项的符号来确定:
负负得正
一正一负得负。
1. 两项相乘时,先定符号。
2.最后的结果要合并同类项.
先化简,再求值:
,其中
,
解:
例2
计算:
(1)(x+2)(x+3)=__________;
(2)(x-4)(x+1)=__________;
(3)(y+4)(y-2)=__________;
(4)(y-5)(y-3)=__________.
x2+5x+6
x2-3x-4
y2+2y-8
y2-8y+15
由上面计算的结果找规律,观察填空:
(x+p)(x+q)=___2+______x+_______.
x
(p+q)
pq
拓展练习
随堂训练
1.下列多项式相乘,结果为x2-4x-12的是( )
A.(x-4)(x+3) B.(x-6)(x+2)
C.(x-4)(x-3) D.(x+6)(x-2)
2.如果(x+a)(x+b)的结果中不含x的一次项,那么a,b
满足 ( )
A.a=b B.a=0
C.a=-b D.b=0
B
C
3.计算:
(1)
(2)
(3)
(4)
解:原式
解:原式
解:原式
解:原式
解:原式
解:原式
4.化简求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中 x=1,y=-2.
解:(4x+3y)(4x-3y)+(2x+y)(3x-5y)
当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2
=22+14 -56
=-20.
5.已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a,b的值.
解: (ax2+bx+1)(3x-2)
=3ax3-2ax2+3bx2-2bx+3x-2
=3ax3+(-2a+3b)x2+(-2b+3)x-2.
∵积不含x2项,也不含x项,
课堂小结
实质:转化为单项式乘多项式的运算
多项式与多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项每一项相乘,再把所得的积相加.
(a+b)(m+n)
am+an+bm+bn
=
