第8章8.4因式分解(第1课时 提公因式法) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第8章8.4因式分解(第1课时 提公因式法) 教学课件--沪科版初中数学七年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:20 | ||
图片预览








文档简介
(共24张PPT)
第 8章 整式乘法与因式分解
8.4 因式分解
第1课时 提公因式法
学 习 目 标
1
2
了解因式分解的意义,理解因式分解的概念及其与整式乘法的区别和联系.(重点)
理解提公因式法并能熟练地运用提公因式法分解因式.(难点)
回顾小学学过的因数分解:
6=2×3
60=2×2×3×5
像这样,把一个多项式化成几个因式乘积的形式,叫做 因式分解
类似地,在整式中,也可以把一个多项式化成几个因式乘积的形式,如:
ma+ma=m×(a+b)
知识讲解
因式分解的概念
计算下列各式:
(1) x(x+1)= ;
(2) (x+1)(x-1)= ;
(3) (a+b)2 = .
x2 +x
x2 -1
a2 +2ab+b2
把下列多项式写成整式的乘积的形式:
(1) x2 +x=( )( )
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2
x x+1
x+1 x-1
a+b
整式乘法
?
整式的乘法和因式分解的关系
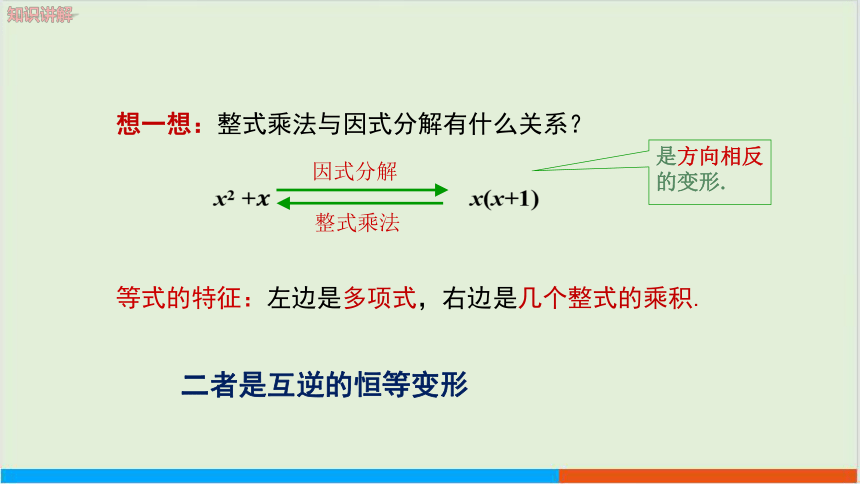
x2 + x(x+1)
因式分解
整式乘法
等式的特征:左边是多项式,右边是几个整式的乘积.
想一想:整式乘法与因式分解有什么关系?
是方向相反的变形.
二者是互逆的恒等变形
判断一个式子是不是因式分解,要看等式的左边是不是一个多项式,右边是不是几个整式的积的形式.
试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)( )
(3)( )
(4) ( )
(1)分解因式是多项式的恒等变形,也就是分解因式的结果的积等于多项式;
(2)分解因式的结果必须是整式的积的形式,每个因式必须是整式且每个因式的次数都不高于原来多项式的次数.
(3)因式分解必须分解到每一个因式都不能再分解为止.
注意:
多项式ma+mb有什么特点?
各项都含有一个公共的因式
例如:是多项式各项的公因式;
是多项式各项的公因式.
观察:
公因式
我们把多项式各项都含有的相同因式,叫做这个多项式的公因式。如ab+bc的公因式是b。
3.看字母的指数:各相同字母的指数取指数最低的;
1.看系数:若各项系数都是整数,应提取各项系数的最大公因数;
2.看字母:公因式的字母是各项相同的字母;
确定公因式的基本步骤
4.看整体:若多项式中含有相同的多项式,应将其看成整体,不要拆开.
提示:当多项式的首项系数为负数时,通常取公因式的系数为负。
说出下列多项式各项的公因式:
(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)-2a2b-2ab2+ab .
练一练:
m
4k
5y2
-ab
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
例如:
提公因式法分解因式
提公因式法分解因式的一般步骤:
(1)确定公因式:先确定系数,再确定字母和字 母的指数;
(2)提公因式并确定另一个因式;
(3)把多项式写成这两个因式的积的形式.
例1
把下列各式分解因式.
=
=
把分解因式.
例2
=2
解:原式=
例3
其中=-5, =3.
先分解因式,再求值.
解:
=
当=-5, =3时,
原式=(3+7)〔4×(-5)2-3〕
=10×(100 -3)
=970.
随堂训练
1.下列各式由左边到右边的变形中,属于分解因式的是 ( )
A.a(x+y)=ax+ay
B.x2-4x+4=x(x-4)+4
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x
解析: A.是多项式乘法,故选项错误;B.右边不是积的形式,故选项错误;C.提公因式法,故选项正确;D.右边不是积的形式,故选项错误.故选C.
C
2.设x2+3x+y=(x+1)(x+2),则y的值为 ( )
A.1 B.2 C.3 D.4
B
3.观察下列各式:①2a+b和a+b ;②5m(a-b)和-a+b ;③3(a+b)和-a-b ;④x2-y2和x2+y2.其中有公因式的是 ( )
A.①② B.②③
C.③④ D.①④
B
4.用提公因式法分解因式.
(1)4x2- 4xy+8xz ;
(2)6x4- 4x3+2x2 ;
(3)6m2n-15mn2+30m3n ;
(4)(a+b)-(a+b)2 ;
(5)x(x-y)+y (y-x) ;
(6)(m+n)2-2(m+n) .
解: (1)4x2- 4xy+8xz=4x(x-y+2z).
(2)6x4- 4x3+2x2=2x2(3x2-2x+1).
(3)6m2n-15mn2+30m2n=3mn(2m-5n+10m2).
(4)(a+b)-(a+b)2=(a+b)(1-a-b).
(5)x(x-y)+y(y-x)=x(x-y)-y(x-y)=(x-y)2.
(6)(m+n)2-2(m+n)=(m+n)(m+n-2).
解:
=
=5×(4-1)
=15.
5.已知,,求的值.
6.计算:
(1)39×37-13×91;
(2)29×20.18+72×20.18+13×20.18-20.18×14.
(2)原式=20.18×(29+72+13-14)=2018.
=13×20=260.
解:(1)原式=3×13×37-13×91
=13×(3×37-91)
7.20042+2004能被2005整除吗
解: ∵20042+2004
=2004(2004+1)
=2004×2005,
∴ 20042+2004能被2005整除.
(1)因式分解与整式的乘法是一种互逆关系;
(2)因式分解的对象必须是多项式,结果要以积的形式表示;
(3)分解后的每个因式必须是整式,
(4)提取公因式法,有时要将相同的括号整体看成一个因式。
课堂小结
(1)当多项式的各项系数都是整数时,取各项系数的最大公约数作公因式的系数;
(2)取多项式各项相同因式的最低次幂的积作公因式中的因式;
(3)当多项式的首项系数为负数时,通常取公因式的系数为负.
提取公因式的注意事项:
第 8章 整式乘法与因式分解
8.4 因式分解
第1课时 提公因式法
学 习 目 标
1
2
了解因式分解的意义,理解因式分解的概念及其与整式乘法的区别和联系.(重点)
理解提公因式法并能熟练地运用提公因式法分解因式.(难点)
回顾小学学过的因数分解:
6=2×3
60=2×2×3×5
像这样,把一个多项式化成几个因式乘积的形式,叫做 因式分解
类似地,在整式中,也可以把一个多项式化成几个因式乘积的形式,如:
ma+ma=m×(a+b)
知识讲解
因式分解的概念
计算下列各式:
(1) x(x+1)= ;
(2) (x+1)(x-1)= ;
(3) (a+b)2 = .
x2 +x
x2 -1
a2 +2ab+b2
把下列多项式写成整式的乘积的形式:
(1) x2 +x=( )( )
(2) x2 -1 =( )( )
(3) a2 +2ab+b2 =( )2
x x+1
x+1 x-1
a+b
整式乘法
?
整式的乘法和因式分解的关系
x2 + x(x+1)
因式分解
整式乘法
等式的特征:左边是多项式,右边是几个整式的乘积.
想一想:整式乘法与因式分解有什么关系?
是方向相反的变形.
二者是互逆的恒等变形
判断一个式子是不是因式分解,要看等式的左边是不是一个多项式,右边是不是几个整式的积的形式.
试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)( )
(3)( )
(4) ( )
(1)分解因式是多项式的恒等变形,也就是分解因式的结果的积等于多项式;
(2)分解因式的结果必须是整式的积的形式,每个因式必须是整式且每个因式的次数都不高于原来多项式的次数.
(3)因式分解必须分解到每一个因式都不能再分解为止.
注意:
多项式ma+mb有什么特点?
各项都含有一个公共的因式
例如:是多项式各项的公因式;
是多项式各项的公因式.
观察:
公因式
我们把多项式各项都含有的相同因式,叫做这个多项式的公因式。如ab+bc的公因式是b。
3.看字母的指数:各相同字母的指数取指数最低的;
1.看系数:若各项系数都是整数,应提取各项系数的最大公因数;
2.看字母:公因式的字母是各项相同的字母;
确定公因式的基本步骤
4.看整体:若多项式中含有相同的多项式,应将其看成整体,不要拆开.
提示:当多项式的首项系数为负数时,通常取公因式的系数为负。
说出下列多项式各项的公因式:
(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)-2a2b-2ab2+ab .
练一练:
m
4k
5y2
-ab
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
例如:
提公因式法分解因式
提公因式法分解因式的一般步骤:
(1)确定公因式:先确定系数,再确定字母和字 母的指数;
(2)提公因式并确定另一个因式;
(3)把多项式写成这两个因式的积的形式.
例1
把下列各式分解因式.
=
=
把分解因式.
例2
=2
解:原式=
例3
其中=-5, =3.
先分解因式,再求值.
解:
=
当=-5, =3时,
原式=(3+7)〔4×(-5)2-3〕
=10×(100 -3)
=970.
随堂训练
1.下列各式由左边到右边的变形中,属于分解因式的是 ( )
A.a(x+y)=ax+ay
B.x2-4x+4=x(x-4)+4
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x
解析: A.是多项式乘法,故选项错误;B.右边不是积的形式,故选项错误;C.提公因式法,故选项正确;D.右边不是积的形式,故选项错误.故选C.
C
2.设x2+3x+y=(x+1)(x+2),则y的值为 ( )
A.1 B.2 C.3 D.4
B
3.观察下列各式:①2a+b和a+b ;②5m(a-b)和-a+b ;③3(a+b)和-a-b ;④x2-y2和x2+y2.其中有公因式的是 ( )
A.①② B.②③
C.③④ D.①④
B
4.用提公因式法分解因式.
(1)4x2- 4xy+8xz ;
(2)6x4- 4x3+2x2 ;
(3)6m2n-15mn2+30m3n ;
(4)(a+b)-(a+b)2 ;
(5)x(x-y)+y (y-x) ;
(6)(m+n)2-2(m+n) .
解: (1)4x2- 4xy+8xz=4x(x-y+2z).
(2)6x4- 4x3+2x2=2x2(3x2-2x+1).
(3)6m2n-15mn2+30m2n=3mn(2m-5n+10m2).
(4)(a+b)-(a+b)2=(a+b)(1-a-b).
(5)x(x-y)+y(y-x)=x(x-y)-y(x-y)=(x-y)2.
(6)(m+n)2-2(m+n)=(m+n)(m+n-2).
解:
=
=5×(4-1)
=15.
5.已知,,求的值.
6.计算:
(1)39×37-13×91;
(2)29×20.18+72×20.18+13×20.18-20.18×14.
(2)原式=20.18×(29+72+13-14)=2018.
=13×20=260.
解:(1)原式=3×13×37-13×91
=13×(3×37-91)
7.20042+2004能被2005整除吗
解: ∵20042+2004
=2004(2004+1)
=2004×2005,
∴ 20042+2004能被2005整除.
(1)因式分解与整式的乘法是一种互逆关系;
(2)因式分解的对象必须是多项式,结果要以积的形式表示;
(3)分解后的每个因式必须是整式,
(4)提取公因式法,有时要将相同的括号整体看成一个因式。
课堂小结
(1)当多项式的各项系数都是整数时,取各项系数的最大公约数作公因式的系数;
(2)取多项式各项相同因式的最低次幂的积作公因式中的因式;
(3)当多项式的首项系数为负数时,通常取公因式的系数为负.
提取公因式的注意事项:
