第8章8.4因式分解(第4课时 分组分解法) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第8章8.4因式分解(第4课时 分组分解法) 教学课件--沪科版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:20 | ||
图片预览





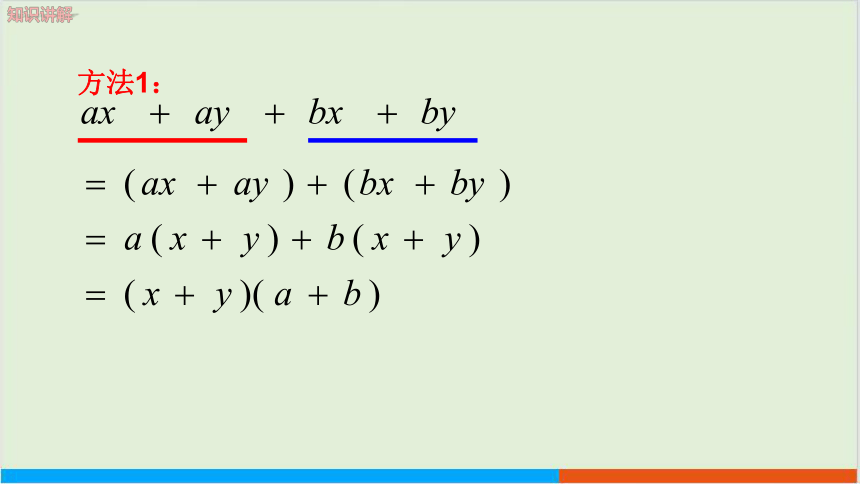



文档简介
(共20张PPT)
第 8 章 整式乘法与因式分解
8.4 因式分解
第4课时 分组分解法
学 习 目 标
1
2
理解并掌握运用分组分解法分解因式的一般步骤.(重点)
能熟练运用分组分解法进行因式分解并解决问题.(难点)
知识回顾
提公因式法:ma+mb+mc=m(a+b+c)
平方差公式法:a2-b2=(a+b)(a-b)
完全平方公式法:
因式分解学过了哪些方法?
把下列式子分解因式:
活动
把下列多项式分解因式
(2)
(1)
请问多项式 如何分解呢?
知识讲解
方法1:
方法2:
1、分组分解:先将多项式分成2个或多个部分分别分解(组内分解),再考虑提公因式法或公式法整体分解(组间分解)。
2、分组不唯一,目的是为了更方便地继续分解因式。
1.分组后能直接提公因式
例 1:把a2-ab+ac-bc分解因式
分析:把这个多项式的四项按前两项与后两项分成两组,分别提出公因式a与c后,另一个因式正好都是a-b,这样就可以提出公因式a-b 。
解:a2-ab+ac-bc
=(a2-ab)+(ac-bc)
=a(a-b)+c(a-b)
=(a-b)(a+c)
——分组
——组内 提公因式
——组 间提公因式
还有没有其他分组的方法;如果有,因式分解的结果是不是一样。
解(2):a2-ab+ac-bc
=(a2+ac)-(ab+bc)
=a(a+c)-b(a+c)
= (a+c)(a-b)
想一想
2. 分组后能直接运用公式
例:把a2+2ab+b2-c2分解因式
分析:经过观察,前三项是一个完全平方式, (a+b)2 与-c2正好又构造为平方差公式的形式,能继续分解。
解:
=(a+b)2-c2
=(a+b+c)(a+b-c)
原式=(a2+2ab+b2)-c2
3、分组后提取公因式和公式法同用
例3 把x2-y2+ax+ay分解因式
分析:把第一、二两项作为一组可以用公式法分解为 (x+y)(x-y);把第三、四项作为一组可以提取公因式a(x+y),这两组正好都有(x+y)的因式,还可以继续分解。
解:x2-y2+ax+ay
= (x2-y2)+(ax+ay)
=(x+y)(x-y)+a(x+y)
= (x+y)(x-y+a)
注意事项:
(1)把有公因式的各项归为一组,并使得各组之间产生新的公因式,这是正确分组的关键所在。因此,分组分解因式要有预见性;
(2)分组的方法不唯一,而合理的选择分组方 案,会使分解过程简单;
(3)分组时要用到添括号法则,注意在添加带有负号的括号时,括号内每项的符号都要改变;
(4)分组只是为实际分解创造了条件, 并没有直接达到分解的目的。
随堂训练
1、多项式 分解因式的结果是( )
A
2、因式分解
下列说法正确的有 (多选)
(1)(2)(3)
3.把下列各式分解因式:
(1)5x2+6y-15x-2xy;
(2)7a2+ab-21a-3b;
(3)ax2+3x2-4a-12;
(4)1-m2-n2+2mn.
4.已知a2+b2-6a+2b+10=0,求a,b的值。
5. 已知a,b,c分别是△ABC三边的长,且a2 + 2b2+c2-2b(a+c)=0,请判断△ABC的形状, 并说明理由.
∴△ABC是等边三角形.
解:△ABC是等边三角形.理由如下:
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,∴a=b=c,
由a2+2b2+c2-2b(a+c)=0,
得 a2-2ab+b2+b2-2bc+c2=0,
课堂小结
把一个多项式的项分组后各组都能运用公式或提取公因式进行分解,那么这个多项式就可以用分组分解法来分解因式
第 8 章 整式乘法与因式分解
8.4 因式分解
第4课时 分组分解法
学 习 目 标
1
2
理解并掌握运用分组分解法分解因式的一般步骤.(重点)
能熟练运用分组分解法进行因式分解并解决问题.(难点)
知识回顾
提公因式法:ma+mb+mc=m(a+b+c)
平方差公式法:a2-b2=(a+b)(a-b)
完全平方公式法:
因式分解学过了哪些方法?
把下列式子分解因式:
活动
把下列多项式分解因式
(2)
(1)
请问多项式 如何分解呢?
知识讲解
方法1:
方法2:
1、分组分解:先将多项式分成2个或多个部分分别分解(组内分解),再考虑提公因式法或公式法整体分解(组间分解)。
2、分组不唯一,目的是为了更方便地继续分解因式。
1.分组后能直接提公因式
例 1:把a2-ab+ac-bc分解因式
分析:把这个多项式的四项按前两项与后两项分成两组,分别提出公因式a与c后,另一个因式正好都是a-b,这样就可以提出公因式a-b 。
解:a2-ab+ac-bc
=(a2-ab)+(ac-bc)
=a(a-b)+c(a-b)
=(a-b)(a+c)
——分组
——组内 提公因式
——组 间提公因式
还有没有其他分组的方法;如果有,因式分解的结果是不是一样。
解(2):a2-ab+ac-bc
=(a2+ac)-(ab+bc)
=a(a+c)-b(a+c)
= (a+c)(a-b)
想一想
2. 分组后能直接运用公式
例:把a2+2ab+b2-c2分解因式
分析:经过观察,前三项是一个完全平方式, (a+b)2 与-c2正好又构造为平方差公式的形式,能继续分解。
解:
=(a+b)2-c2
=(a+b+c)(a+b-c)
原式=(a2+2ab+b2)-c2
3、分组后提取公因式和公式法同用
例3 把x2-y2+ax+ay分解因式
分析:把第一、二两项作为一组可以用公式法分解为 (x+y)(x-y);把第三、四项作为一组可以提取公因式a(x+y),这两组正好都有(x+y)的因式,还可以继续分解。
解:x2-y2+ax+ay
= (x2-y2)+(ax+ay)
=(x+y)(x-y)+a(x+y)
= (x+y)(x-y+a)
注意事项:
(1)把有公因式的各项归为一组,并使得各组之间产生新的公因式,这是正确分组的关键所在。因此,分组分解因式要有预见性;
(2)分组的方法不唯一,而合理的选择分组方 案,会使分解过程简单;
(3)分组时要用到添括号法则,注意在添加带有负号的括号时,括号内每项的符号都要改变;
(4)分组只是为实际分解创造了条件, 并没有直接达到分解的目的。
随堂训练
1、多项式 分解因式的结果是( )
A
2、因式分解
下列说法正确的有 (多选)
(1)(2)(3)
3.把下列各式分解因式:
(1)5x2+6y-15x-2xy;
(2)7a2+ab-21a-3b;
(3)ax2+3x2-4a-12;
(4)1-m2-n2+2mn.
4.已知a2+b2-6a+2b+10=0,求a,b的值。
5. 已知a,b,c分别是△ABC三边的长,且a2 + 2b2+c2-2b(a+c)=0,请判断△ABC的形状, 并说明理由.
∴△ABC是等边三角形.
解:△ABC是等边三角形.理由如下:
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,∴a=b=c,
由a2+2b2+c2-2b(a+c)=0,
得 a2-2ab+b2+b2-2bc+c2=0,
课堂小结
把一个多项式的项分组后各组都能运用公式或提取公因式进行分解,那么这个多项式就可以用分组分解法来分解因式
