第10章10.1相交线 (第1课时 对顶角的概念及性质) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第10章10.1相交线 (第1课时 对顶角的概念及性质) 教学课件--沪科版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:20 | ||
图片预览


文档简介
(共17张PPT)
第10章 相交线、平行线与平移
10.1 相交线
第1课时 对角线的概念及性质
1
学习目标
2
经历探究对顶角、邻补角的位置关系的过程,理解邻补角与对顶角的概念. (重点)
掌握对顶角的性质,并能运用性质进行角的计算及解决简单实际问题.(难点)
新课导入
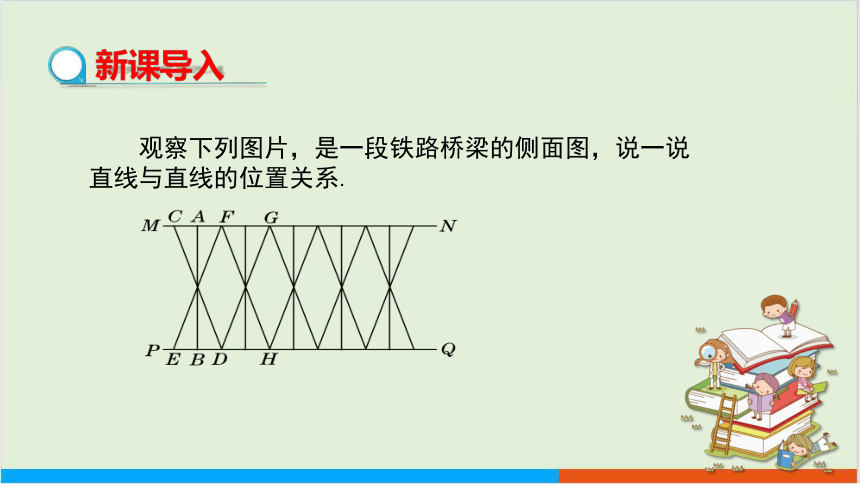
观察下列图片,是一段铁路桥梁的侧面图,说一说直线与直线的位置关系.
知识讲解
一 邻补角和对顶角
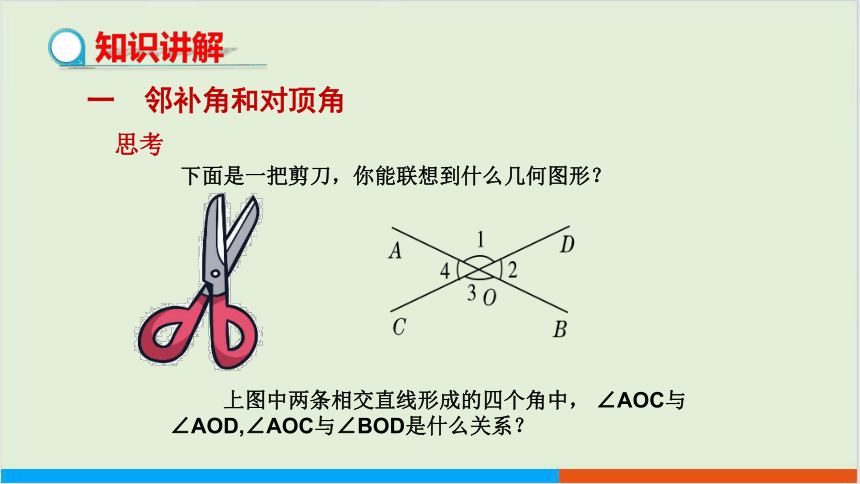
下面是一把剪刀,你能联想到什么几何图形?
思考
上图中两条相交直线形成的四个角中, ∠AOC与∠AOD,∠AOC与∠BOD是什么关系?
知识讲解
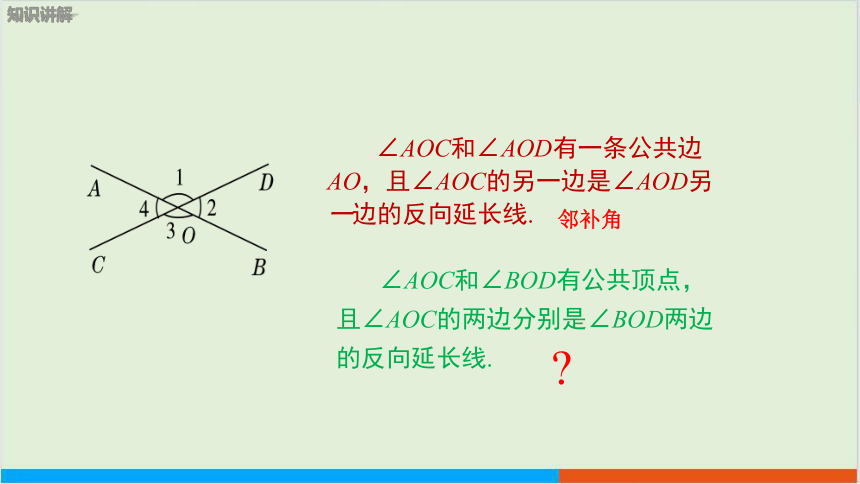
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.
邻补角
知识讲解
1
2
A
B
C
D
O
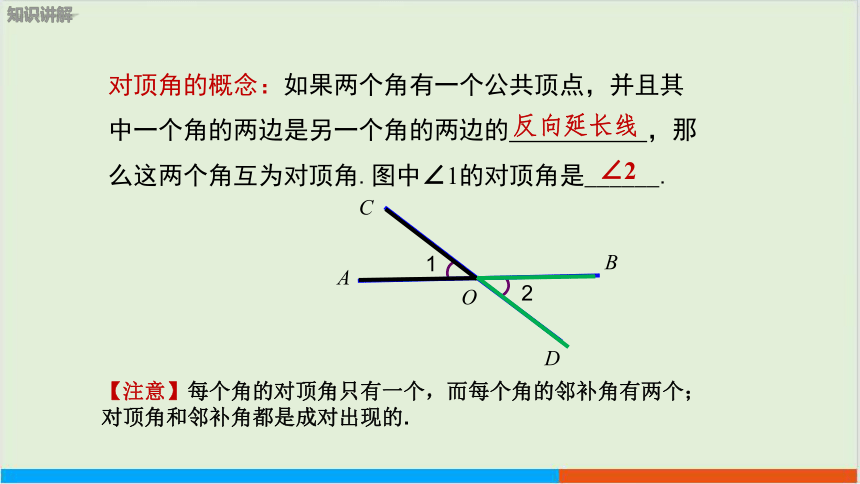
对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
【注意】每个角的对顶角只有一个,而每个角的邻补角有两个;对顶角和邻补角都是成对出现的.
知识讲解
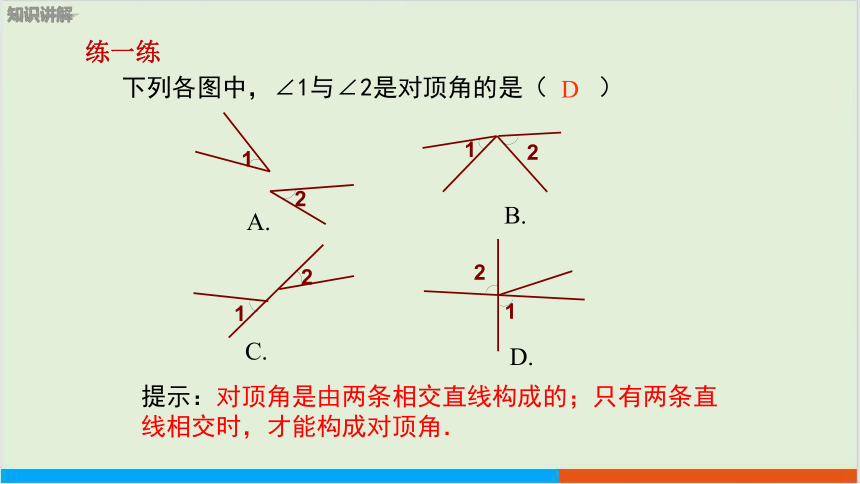
下列各图中,∠1与∠2是对顶角的是( )
1
2
C.
1
2
D.
D
1
2
A.
1
2
B.
提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.
练一练
知识讲解
二 对顶角的性质
A
O
C
B
D
【观察】在用剪刀剪布片的过程中,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.在这过程中,两个把手之间的角与剪刀刃之间的角有什么关系?
知识讲解
猜想:对顶角相等
C
O
A
B
D
4
3
2
1
问题:如图,直线AB和直线CD相交于点O,∠1 与∠3在数量上有什么关系呢?
思考:怎样说明∠1=∠3?
知识讲解
O
A
B
C
D
4
3
2
1
如图,已知:直线AB与CD相交于点O,试说明:∠1=∠3, ∠2=∠4.
解:因为直线AB与CD相交于O点,
所以∠1+∠2=180°
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.
对顶角相等
知识讲解
解:由邻补角的定义,得
∠2=180°-∠1=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4=∠2=140°.
a
b
)
(
1
3
4
2
)
(
例 如图,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
随堂训练
1.如图,点O在直线AB上,射线OC平分∠DOB.
若∠COB35°,则∠AOD等于( )
A.35°
B.70°
C.110°
D.145°
C
2.如图,直线AB与CD相交于点O,已知∠BOD=30°,OE是∠BOC的平分线,则∠EOA= .
105°
随堂训练
3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
解:由对顶角相等,得∠AOC=∠BOD=42°.
因为OA平分∠COE,
所以∠COE=2∠AOC=84°.
由邻补角的性质,得
∠DOE=180°∠COE=180°-84°=96°.
随堂训练
4.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
随堂训练
5. 观察下列各图,寻找对顶角(不含平角)
⑴ 如图1,图中共有 对对顶角;
⑵ 如图2,图中共有 对对顶角;
⑶ 如图3,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的
关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有20条直线相交于一点,则可形成 对对顶角.
图1
图2
图3
2
6
12
n(n-1)
380
课堂小结
角的 名称 特 征 性 质 相 同 点 不 同 点
邻补角
对顶角 对顶
角相
等
邻补
角互
补
②有公共顶点;
③有一条公共边
①两条直线相交形成的角;
①两条直线相交而成的角;
②有公共顶点;
③没有公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
第10章 相交线、平行线与平移
10.1 相交线
第1课时 对角线的概念及性质
1
学习目标
2
经历探究对顶角、邻补角的位置关系的过程,理解邻补角与对顶角的概念. (重点)
掌握对顶角的性质,并能运用性质进行角的计算及解决简单实际问题.(难点)
新课导入
观察下列图片,是一段铁路桥梁的侧面图,说一说直线与直线的位置关系.
知识讲解
一 邻补角和对顶角
下面是一把剪刀,你能联想到什么几何图形?
思考
上图中两条相交直线形成的四个角中, ∠AOC与∠AOD,∠AOC与∠BOD是什么关系?
知识讲解
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.
邻补角
知识讲解
1
2
A
B
C
D
O
对顶角的概念:如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠2
【注意】每个角的对顶角只有一个,而每个角的邻补角有两个;对顶角和邻补角都是成对出现的.
知识讲解
下列各图中,∠1与∠2是对顶角的是( )
1
2
C.
1
2
D.
D
1
2
A.
1
2
B.
提示:对顶角是由两条相交直线构成的;只有两条直线相交时,才能构成对顶角.
练一练
知识讲解
二 对顶角的性质
A
O
C
B
D
【观察】在用剪刀剪布片的过程中,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.在这过程中,两个把手之间的角与剪刀刃之间的角有什么关系?
知识讲解
猜想:对顶角相等
C
O
A
B
D
4
3
2
1
问题:如图,直线AB和直线CD相交于点O,∠1 与∠3在数量上有什么关系呢?
思考:怎样说明∠1=∠3?
知识讲解
O
A
B
C
D
4
3
2
1
如图,已知:直线AB与CD相交于点O,试说明:∠1=∠3, ∠2=∠4.
解:因为直线AB与CD相交于O点,
所以∠1+∠2=180°
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.
对顶角相等
知识讲解
解:由邻补角的定义,得
∠2=180°-∠1=140°;
由对顶角相等,得
∠3=∠1=40°,
∠4=∠2=140°.
a
b
)
(
1
3
4
2
)
(
例 如图,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
随堂训练
1.如图,点O在直线AB上,射线OC平分∠DOB.
若∠COB35°,则∠AOD等于( )
A.35°
B.70°
C.110°
D.145°
C
2.如图,直线AB与CD相交于点O,已知∠BOD=30°,OE是∠BOC的平分线,则∠EOA= .
105°
随堂训练
3.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
解:由对顶角相等,得∠AOC=∠BOD=42°.
因为OA平分∠COE,
所以∠COE=2∠AOC=84°.
由邻补角的性质,得
∠DOE=180°∠COE=180°-84°=96°.
随堂训练
4.如图,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
解:(1)∠BOE=180°-∠AOC-∠COE=180°-36°-90°=54°.
(2)因为∠BOD∶∠BOC=1∶5,∠BOD+∠BOC=180°,
所以∠BOD=30°.
因为∠AOC=∠BOD,
所以∠AOC=30°,
所以∠AOE=∠COE+∠AOC=90°+30°=120°.
随堂训练
5. 观察下列各图,寻找对顶角(不含平角)
⑴ 如图1,图中共有 对对顶角;
⑵ 如图2,图中共有 对对顶角;
⑶ 如图3,图中共有 对对顶角;
⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的
关系,猜测:若有n条直线相交于一点,则可形成
对对顶角;
⑸ 若有20条直线相交于一点,则可形成 对对顶角.
图1
图2
图3
2
6
12
n(n-1)
380
课堂小结
角的 名称 特 征 性 质 相 同 点 不 同 点
邻补角
对顶角 对顶
角相
等
邻补
角互
补
②有公共顶点;
③有一条公共边
①两条直线相交形成的角;
①两条直线相交而成的角;
②有公共顶点;
③没有公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
