第10章10.1相交线 (第2课时 垂线的概念、画法及性质) 教学课件--沪科版初中数学七年级(下)
文档属性
| 名称 | 第10章10.1相交线 (第2课时 垂线的概念、画法及性质) 教学课件--沪科版初中数学七年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:20 | ||
图片预览





文档简介
(共23张PPT)
第10章 相交线、平行线与平移
10.1 相交线
第2课时 垂线的概念、画法及性质
1
学习目标
2
理解垂线的有关概念及性质.(重点)
会用三角尺过一点画已知直线的垂线. (难点)
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
知识讲解
一 垂线的概念
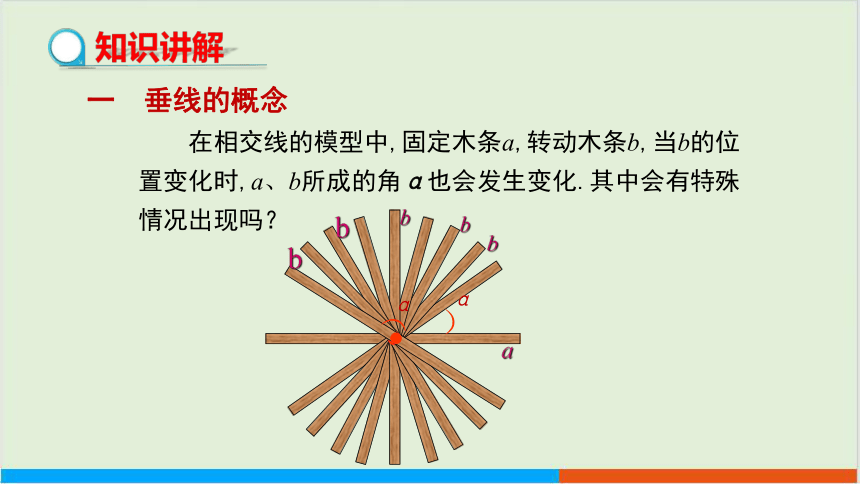
在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角α也会发生变化.其中会有特殊情况出现吗?
)
α
a
b
b
b
b
b
)
α
知识讲解
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、
∠BOC的度数是多少?为什么?
A
B
C
D
O
由对顶角和邻补角的性质知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
知识讲解
垂线的概念
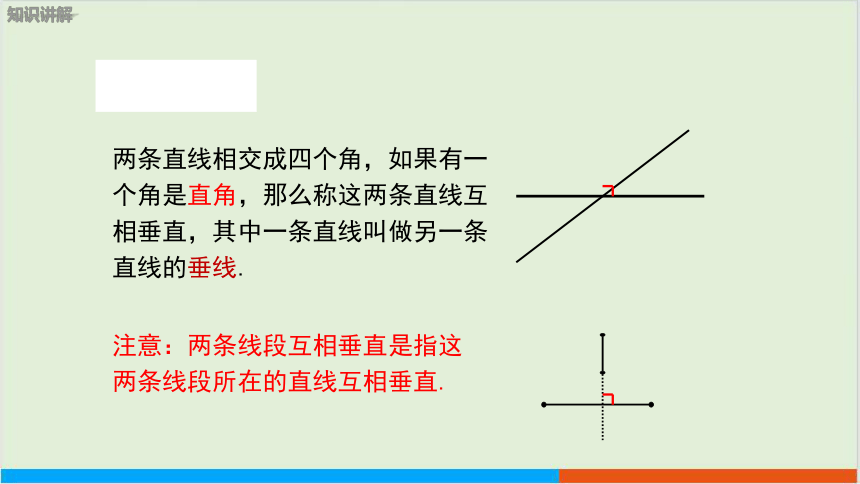
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
知识讲解
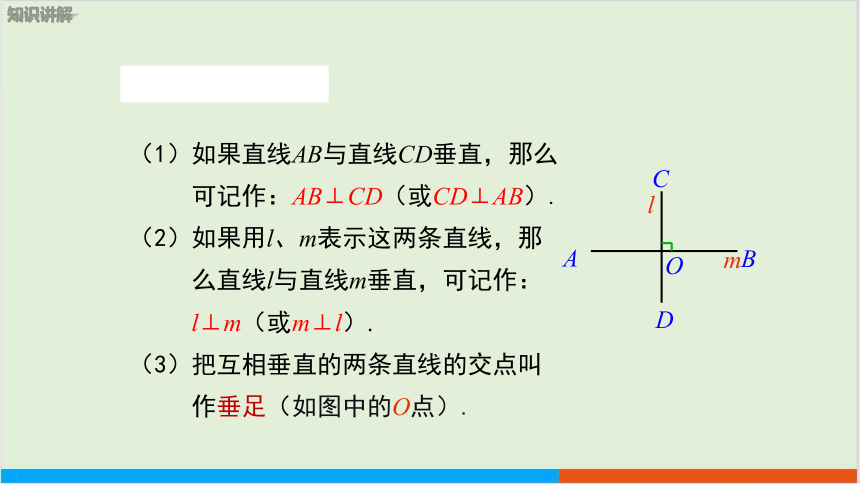
(1)如果直线AB与直线CD垂直,那么
可记作:AB⊥CD(或CD⊥AB).
(2)如果用l、m表示这两条直线,那
么直线l与直线m垂直,可记作:
l⊥m(或m⊥l).
(3)把互相垂直的两条直线的交点叫
作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示方法
知识讲解
A
B
C
D
O
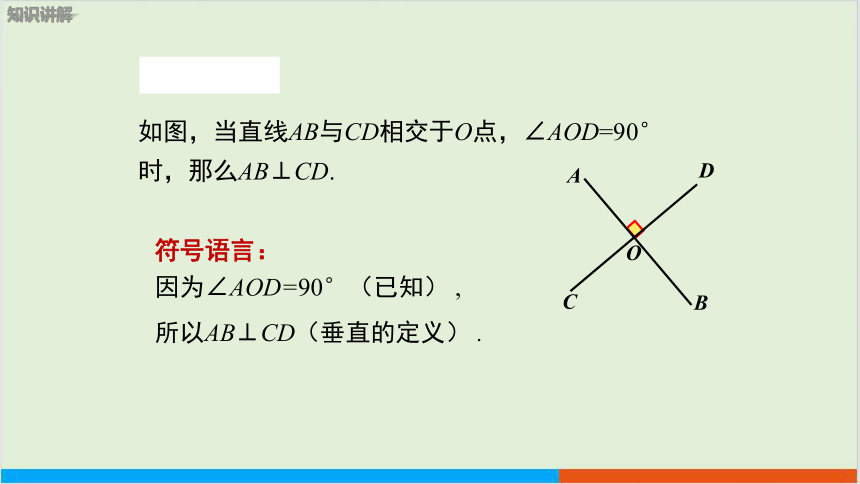
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD.
因为∠AOD=90°(已知) ,
所以AB⊥CD(垂直的定义) .
垂线的判定
知识讲解
思考
下面所叙述的两条直线是否垂直?
1.两条直线相交所成的四个角相等;
2.两条直线相交,有一组邻补角相等;
3.两条直线相交,对顶角互补.
结论:都是垂直的.
知识讲解
二 垂线的画法及性质
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
操作
知识讲解
折一折
你能用纸折出两条互相垂直的直线吗
知识讲解
l
A
一靠(线),
二过(点),
三画(线)
通过上面的操作,你能总结出用三角尺画垂线的方法吗?
若点在直线外,操作方法是一样的
知识讲解
思考:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
A
.B
l
.
知识讲解
问题 这样画l的垂线可以画几条?
l
O
(1)如图,已知直线 l,作l的垂线.
A
无数条
知识讲解
l
A
问题 这样画l的垂线可以画几条?
一条
(2)如图,已知直线 l 和l上的一点A ,作l的垂线.
知识讲解
l
A
B
根据以上操作,你能得出什么结论?
问题 这样画l的垂线可以画几条?
一条
(3)如图,已知直线 l 和l外的一点A ,作l的垂线.
知识讲解
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质
随堂训练
1.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等
B.互余
C.互补
D.互为对顶角
B
随堂训练
2.如图,直线AB、CD相交于点E,EF⊥AB于E,若
∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
随堂训练
3. (1)如图1,若直线m、n相交于点O,∠1=90°,
则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶3,那么∠COA=____ ,∠BOC的补角
为 .
O
a
b
1
B
C
A
O
a⊥b
90°
60°
150°
图1
图2
随堂训练
4.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:因为∠BOE=∠NOE,
所以∠BON=2∠EON=40°,
所以∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
因为AO⊥BC,
所以∠AOC=90°,
所以∠AOM=∠AOC-∠MOC=90°-40°=50°,
综上∠NOC=140°,∠AOM=50°.
课堂小结
1.垂线的概念:
两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
2.垂线的画法:
一靠(线),二过(点),三画(线).
3.垂线的性质:
过一点有且只有一条直线与已知直线垂直.
第10章 相交线、平行线与平移
10.1 相交线
第2课时 垂线的概念、画法及性质
1
学习目标
2
理解垂线的有关概念及性质.(重点)
会用三角尺过一点画已知直线的垂线. (难点)
新课导入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
知识讲解
一 垂线的概念
在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的角α也会发生变化.其中会有特殊情况出现吗?
)
α
a
b
b
b
b
b
)
α
知识讲解
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、
∠BOC的度数是多少?为什么?
A
B
C
D
O
由对顶角和邻补角的性质知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
知识讲解
垂线的概念
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.
知识讲解
(1)如果直线AB与直线CD垂直,那么
可记作:AB⊥CD(或CD⊥AB).
(2)如果用l、m表示这两条直线,那
么直线l与直线m垂直,可记作:
l⊥m(或m⊥l).
(3)把互相垂直的两条直线的交点叫
作垂足(如图中的O点).
A
B
C
D
O
l
m
垂直的表示方法
知识讲解
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD.
因为∠AOD=90°(已知) ,
所以AB⊥CD(垂直的定义) .
垂线的判定
知识讲解
思考
下面所叙述的两条直线是否垂直?
1.两条直线相交所成的四个角相等;
2.两条直线相交,有一组邻补角相等;
3.两条直线相交,对顶角互补.
结论:都是垂直的.
知识讲解
二 垂线的画法及性质
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
操作
知识讲解
折一折
你能用纸折出两条互相垂直的直线吗
知识讲解
l
A
一靠(线),
二过(点),
三画(线)
通过上面的操作,你能总结出用三角尺画垂线的方法吗?
若点在直线外,操作方法是一样的
知识讲解
思考:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能
画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能
画几条
A
.B
l
.
知识讲解
问题 这样画l的垂线可以画几条?
l
O
(1)如图,已知直线 l,作l的垂线.
A
无数条
知识讲解
l
A
问题 这样画l的垂线可以画几条?
一条
(2)如图,已知直线 l 和l上的一点A ,作l的垂线.
知识讲解
l
A
B
根据以上操作,你能得出什么结论?
问题 这样画l的垂线可以画几条?
一条
(3)如图,已知直线 l 和l外的一点A ,作l的垂线.
知识讲解
注意:
1.“过一点”中的点,可以在已知直线上,也可
以在已知直线外;
2.“有且只有”中,“有”指存在,“只有”指
唯一性.
在同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质
随堂训练
1.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等
B.互余
C.互补
D.互为对顶角
B
随堂训练
2.如图,直线AB、CD相交于点E,EF⊥AB于E,若
∠CEF=58°,则∠BED的度数为 .
C
A
B
E
F
D
32°
随堂训练
3. (1)如图1,若直线m、n相交于点O,∠1=90°,
则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则
∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比
为1∶3,那么∠COA=____ ,∠BOC的补角
为 .
O
a
b
1
B
C
A
O
a⊥b
90°
60°
150°
图1
图2
随堂训练
4.如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:因为∠BOE=∠NOE,
所以∠BON=2∠EON=40°,
所以∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
因为AO⊥BC,
所以∠AOC=90°,
所以∠AOM=∠AOC-∠MOC=90°-40°=50°,
综上∠NOC=140°,∠AOM=50°.
课堂小结
1.垂线的概念:
两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
2.垂线的画法:
一靠(线),二过(点),三画(线).
3.垂线的性质:
过一点有且只有一条直线与已知直线垂直.
