10.2 直方图 教学课件--人教版初中数学七年级下
文档属性
| 名称 | 10.2 直方图 教学课件--人教版初中数学七年级下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
10.2 直方图
第 十 章 数据的收集、整理与描述
第十章 数据的收集、整理与描述
掌握用频数分布直方图描述数据分布情况的基本步骤;(重点)
能利用简单的频数分布直方图解释数据中蕴含的信息,对实际问题作出判断和决策,初步建立统计概念.(难点)
1
2
学习目标
温故知新
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
知识讲解
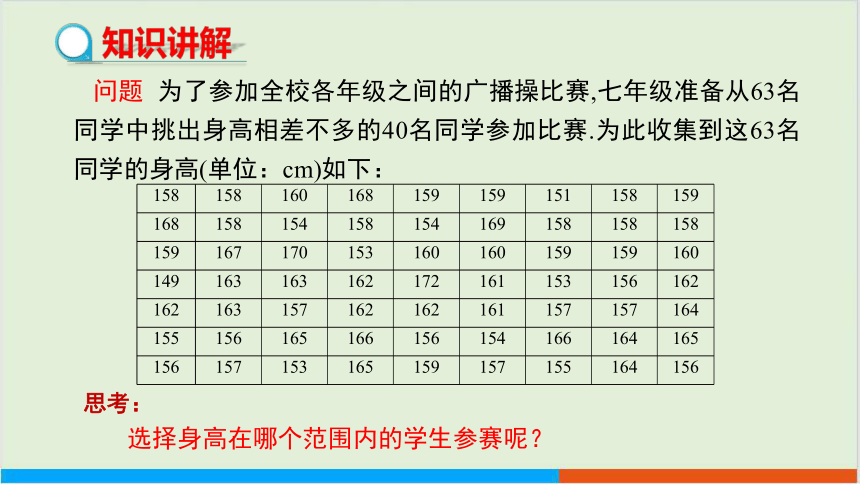
问题 为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
思考:
选择身高在哪个范围内的学生参赛呢?
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
为了使选取的参赛选手身高比较整齐,你知道怎样做才能知道数据(身高)的分布情况?(即在哪些身高范围的学生比较多?哪些身高范围内的学生比较少.)
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3 cm 作为一个组,那么由于
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
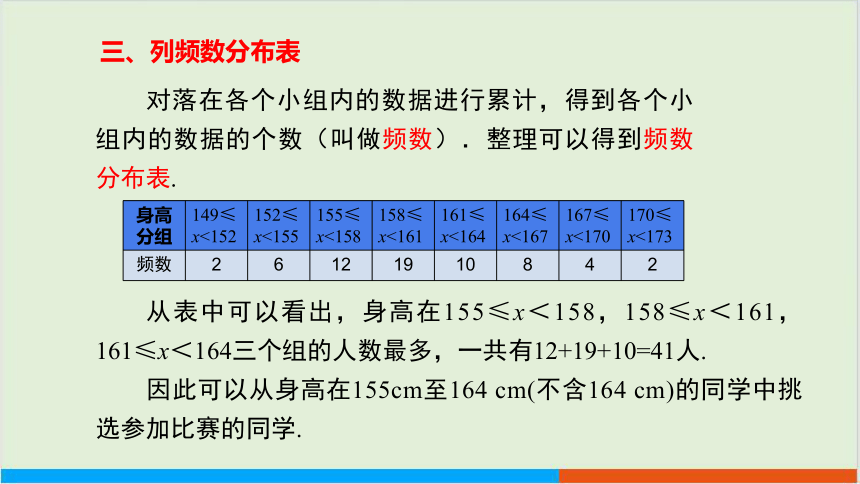
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41人.
因此可以从身高在155cm至164 cm(不含164 cm)的同学中挑选参加比赛的同学.
身高分组 149≤x<152 152≤x<155 155≤x<158 158≤x<161 161≤x<164 164≤x<167 167≤x<170 170≤x<173
频数 2 6 12 19 10 8 4 2
三、列频数分布表
探究
上面我们选取的组距是3,从而把数据分成8组,如果组距取2或4,那么数据分成几个组?这样能否选出需要的40名同学呢?
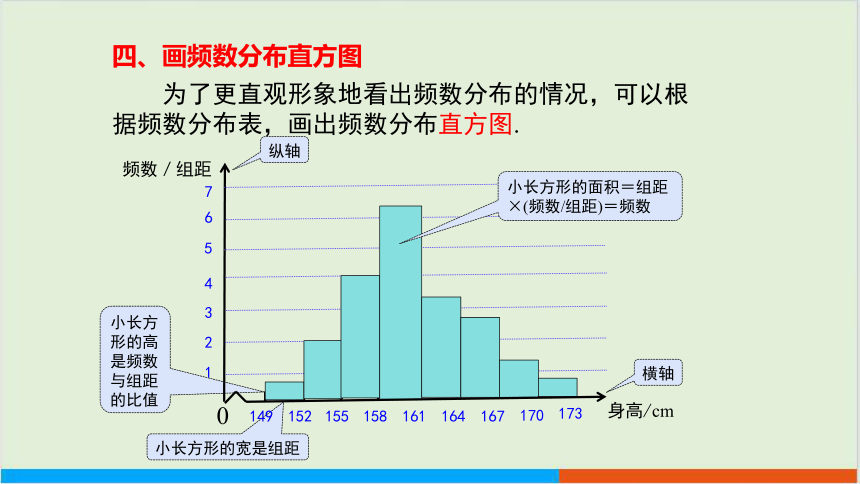
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
横轴
纵轴
小长方形的面积=组距×(频数/组距)=频数
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图的方便,通常直接用小长方形的高作为频数.
频数
(学生人数)
0
149
152
155
158
161
164
167
170
173
5
10
身高/cm
15
20
讨论
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
归纳
制作频数分布直方图的一般步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100
以内,一般分5至12组)
典例剖析
为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4
(2)决定组距和组数
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
(3)列频数分布表
见教材第148页表10-4.
(4)画频数分布直方图
见教材第149页图10.2-3.
获取信息
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他范围较少.长度在5.8≤x<6.1范围内的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6, 4.6≤x<4.9, 7.0≤x<7.3, 7.3≤x<7.6范围内的麦穗根数很少,总共只有7根.
随堂训练
1.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1 000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
解析:由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-8-24-30-10=28,占抽查学生的比例为28÷100×100%=28%.采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280.
2.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有( )
A.6人
B.8人
C.16人
D.20人
D
解析:从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,即各组频数之比为1∶4∶3∶2.一分钟跳绳次数在100次以上的即第三、四组,所占比例为.故有40×20(人).
3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则下列说法:① 该班有50名同学参赛;② 第五组的百分比为16%;③ 成绩在70~80分的人数最多;④ 80分以上的学生有14名,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
解析:第五组所占的百分比是14%12%40%28%16%,故②正确;
该班参赛学生数是8÷16%50(名),故①正确;
从直方图可以直接看出成绩在70~80分的人数最多,故③正确;
80分以上的学生有50×(28%16%)22(名),故④错误.
其中正确的有①②③,共3个.
4、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 。
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课堂小结
制作频数分布直方图
1.计算最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
10.2 直方图
第 十 章 数据的收集、整理与描述
第十章 数据的收集、整理与描述
掌握用频数分布直方图描述数据分布情况的基本步骤;(重点)
能利用简单的频数分布直方图解释数据中蕴含的信息,对实际问题作出判断和决策,初步建立统计概念.(难点)
1
2
学习目标
温故知新
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
知识讲解
问题 为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
思考:
选择身高在哪个范围内的学生参赛呢?
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
为了使选取的参赛选手身高比较整齐,你知道怎样做才能知道数据(身高)的分布情况?(即在哪些身高范围的学生比较多?哪些身高范围内的学生比较少.)
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3 cm 作为一个组,那么由于
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41人.
因此可以从身高在155cm至164 cm(不含164 cm)的同学中挑选参加比赛的同学.
身高分组 149≤x<152 152≤x<155 155≤x<158 158≤x<161 161≤x<164 164≤x<167 167≤x<170 170≤x<173
频数 2 6 12 19 10 8 4 2
三、列频数分布表
探究
上面我们选取的组距是3,从而把数据分成8组,如果组距取2或4,那么数据分成几个组?这样能否选出需要的40名同学呢?
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
横轴
纵轴
小长方形的面积=组距×(频数/组距)=频数
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图的方便,通常直接用小长方形的高作为频数.
频数
(学生人数)
0
149
152
155
158
161
164
167
170
173
5
10
身高/cm
15
20
讨论
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
归纳
制作频数分布直方图的一般步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100
以内,一般分5至12组)
典例剖析
为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4
(2)决定组距和组数
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
(3)列频数分布表
见教材第148页表10-4.
(4)画频数分布直方图
见教材第149页图10.2-3.
获取信息
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他范围较少.长度在5.8≤x<6.1范围内的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6, 4.6≤x<4.9, 7.0≤x<7.3, 7.3≤x<7.6范围内的麦穗根数很少,总共只有7根.
随堂训练
1.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1 000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
解析:由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-8-24-30-10=28,占抽查学生的比例为28÷100×100%=28%.采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280.
2.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有( )
A.6人
B.8人
C.16人
D.20人
D
解析:从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,即各组频数之比为1∶4∶3∶2.一分钟跳绳次数在100次以上的即第三、四组,所占比例为.故有40×20(人).
3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则下列说法:① 该班有50名同学参赛;② 第五组的百分比为16%;③ 成绩在70~80分的人数最多;④ 80分以上的学生有14名,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
解析:第五组所占的百分比是14%12%40%28%16%,故②正确;
该班参赛学生数是8÷16%50(名),故①正确;
从直方图可以直接看出成绩在70~80分的人数最多,故③正确;
80分以上的学生有50×(28%16%)22(名),故④错误.
其中正确的有①②③,共3个.
4、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 。
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课堂小结
制作频数分布直方图
1.计算最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
