17.2函数的图象(2.函数的图象) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 17.2函数的图象(2.函数的图象) 教学课件--华师大版数学八年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:57 | ||
图片预览





文档简介
(共17张PPT)
第17章 函数及其图象
17.2 函数的图象
第17章 函数及其图象
2.函数的图象
学习目标
1.理解函数的图象是由许多点按照一定规律组成的图形,能够在平面直角坐标系内画出简单函数的图象.(重点)
2.通过观察函数的图象,深刻领会函数中两个变量的关系,能够从所给的图象中获取信息,从而解答一些简单的实际问题.(难点)
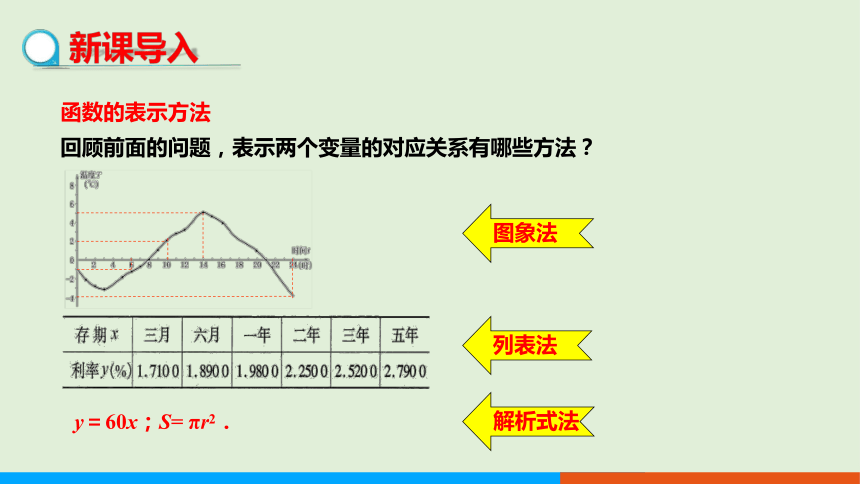
函数的表示方法
回顾前面的问题,表示两个变量的对应关系有哪些方法?
y=60x;S= πr2.
列表法
图象法
解析式法
新课导入
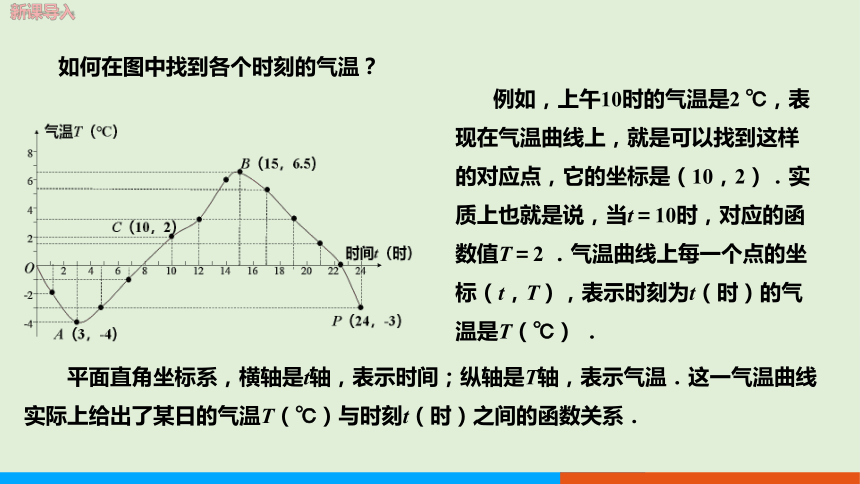
如何在图中找到各个时刻的气温?
平面直角坐标系,横轴是t轴,表示时间;纵轴是T轴,表示气温.这一气温曲线实际上给出了某日的气温T(℃)与时刻t(时)之间的函数关系.
例如,上午10时的气温是2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10,2).实质上也就是说,当t=10时,对应的函数值T=2 .气温曲线上每一个点的坐标(t,T),表示时刻为t(时)的气温是T(℃) .
新课导入
一般来说,函数的图象是由直角坐标系中的一系列点组成.图象上每一点的坐标(x,y)代表了函数的一对对应值.即点的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值.
列表(所取的数值必须符合函数自变量的取值范围);
描点(借助虚线在平面中正确描出对应的点);
连线(必须用光滑的曲线连接起来).
画出简单函数的图象的步骤是什么?
知识讲解
1.函数的图象
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.要画出一个函数的图象,关键是要画出图象上的一些点.为此,首先在自变量x的取值范围内,适当取一些自变量的值,并求出对应的函数值y ,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
知识讲解
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
2
0.5
0
0.5
2
4.5
由以上一系列有序实数对(坐标)在坐标系中描出对应点.
最后,用光滑的曲线连线,就可得函数的图象了.
知识讲解
画函数图象经过哪些步骤
画图象的步骤可以概括为三步:
列表、描点、连线,这种画函数图象的方法叫做描点法.
知识讲解
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷,两人都爬上了山顶.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)之间的函数关系(从小强开始爬山时计时),看图回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
(4) 谁的速度大,大多少?
知识讲解
解:由图象可知:
(1)小强出发0分钟时,爷爷已经爬山60米,
因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,
所以小强用了8分钟追上爷爷;
(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山
(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此,小强的速度大,大7米/分.
知识讲解
1.画函数图象的方法,可以概括为_______, _______ ,_______三步,通常称为_______ .
2.若点A(a,-3)在函数y= 的图象上,则a=____;
3 .下列各点M(1,2),N(3, ),P(1,-1),Q(-2,-4)中,在函数y= 的图象上的是__________.
列表
描点
连线
描点法
1
点N
当堂检测
4.如果点M在函数y=x-1的图象上,则M点的坐标可以是( )
A.(-1,0) B.(0,1) C.(1,0) D.(1,-1)
5.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
C
D
当堂检测
6. 小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
B
当堂检测
7、画出函数y= - 的图象.
解:列表如下:
x … -4 -3 -2 -1 … 1 2 3 4 …
y … 1.5 2 3 6 … -6 -3 -2 -1.5 …
描点,
最后,用光滑的曲线连线,就可得函数的图象了.
当堂检测
8、李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以100米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
解:(1)李老师停留地点离他家路程为:2000-900=1100(米),900÷45=20(分).a=20,b=1100,c=20+30=50.
(2)20+30+11=61(分).答:李老师从学校到家共用61分钟.
当堂检测
课堂小结
1.函数图象上的点的坐标是函数的自变量与函数值的一对对应值.
2.根据列表、描点、连线这三个步骤画出简单函数的图象.
3.通过实际问题的函数图象获取信息.
第17章 函数及其图象
17.2 函数的图象
第17章 函数及其图象
2.函数的图象
学习目标
1.理解函数的图象是由许多点按照一定规律组成的图形,能够在平面直角坐标系内画出简单函数的图象.(重点)
2.通过观察函数的图象,深刻领会函数中两个变量的关系,能够从所给的图象中获取信息,从而解答一些简单的实际问题.(难点)
函数的表示方法
回顾前面的问题,表示两个变量的对应关系有哪些方法?
y=60x;S= πr2.
列表法
图象法
解析式法
新课导入
如何在图中找到各个时刻的气温?
平面直角坐标系,横轴是t轴,表示时间;纵轴是T轴,表示气温.这一气温曲线实际上给出了某日的气温T(℃)与时刻t(时)之间的函数关系.
例如,上午10时的气温是2 ℃,表现在气温曲线上,就是可以找到这样的对应点,它的坐标是(10,2).实质上也就是说,当t=10时,对应的函数值T=2 .气温曲线上每一个点的坐标(t,T),表示时刻为t(时)的气温是T(℃) .
新课导入
一般来说,函数的图象是由直角坐标系中的一系列点组成.图象上每一点的坐标(x,y)代表了函数的一对对应值.即点的横坐标x表示自变量的某一个值,纵坐标y表示与它对应的函数值.
列表(所取的数值必须符合函数自变量的取值范围);
描点(借助虚线在平面中正确描出对应的点);
连线(必须用光滑的曲线连接起来).
画出简单函数的图象的步骤是什么?
知识讲解
1.函数的图象
例1 画出函数 的图象.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.要画出一个函数的图象,关键是要画出图象上的一些点.为此,首先在自变量x的取值范围内,适当取一些自变量的值,并求出对应的函数值y ,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
知识讲解
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
2
0.5
0
0.5
2
4.5
由以上一系列有序实数对(坐标)在坐标系中描出对应点.
最后,用光滑的曲线连线,就可得函数的图象了.
知识讲解
画函数图象经过哪些步骤
画图象的步骤可以概括为三步:
列表、描点、连线,这种画函数图象的方法叫做描点法.
知识讲解
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷,两人都爬上了山顶.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)之间的函数关系(从小强开始爬山时计时),看图回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
(4) 谁的速度大,大多少?
知识讲解
解:由图象可知:
(1)小强出发0分钟时,爷爷已经爬山60米,
因此小强让爷爷先上60米;
(2)山顶离山脚的距离是300米,小强先爬上山;
(3)因为小强和爷爷路程相等时是8分钟,
所以小强用了8分钟追上爷爷;
(4)小强爬山300米用了10分钟,速度为30米/分,爷爷爬山
(300-60)米=240米,用了10.5分钟,速度约为23米/分,因此,小强的速度大,大7米/分.
知识讲解
1.画函数图象的方法,可以概括为_______, _______ ,_______三步,通常称为_______ .
2.若点A(a,-3)在函数y= 的图象上,则a=____;
3 .下列各点M(1,2),N(3, ),P(1,-1),Q(-2,-4)中,在函数y= 的图象上的是__________.
列表
描点
连线
描点法
1
点N
当堂检测
4.如果点M在函数y=x-1的图象上,则M点的坐标可以是( )
A.(-1,0) B.(0,1) C.(1,0) D.(1,-1)
5.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
C
D
当堂检测
6. 小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是( )
B
当堂检测
7、画出函数y= - 的图象.
解:列表如下:
x … -4 -3 -2 -1 … 1 2 3 4 …
y … 1.5 2 3 6 … -6 -3 -2 -1.5 …
描点,
最后,用光滑的曲线连线,就可得函数的图象了.
当堂检测
8、李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以100米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
解:(1)李老师停留地点离他家路程为:2000-900=1100(米),900÷45=20(分).a=20,b=1100,c=20+30=50.
(2)20+30+11=61(分).答:李老师从学校到家共用61分钟.
当堂检测
课堂小结
1.函数图象上的点的坐标是函数的自变量与函数值的一对对应值.
2.根据列表、描点、连线这三个步骤画出简单函数的图象.
3.通过实际问题的函数图象获取信息.
