18.1平行四边形的性质(第2课时平行四边形对角线的性质) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 18.1平行四边形的性质(第2课时平行四边形对角线的性质) 教学课件--华师大版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第18章 平行四边形
18.1 平行四边形的性质
第18章 平行四边形
第2课时 平行四边形对角线的性质
学习目标
1.理解和掌握发现平行四边形的对角线互相平分的特征;(重点)
2.会利用平行四边形的特征进行相关的计算和说理.(难点)
A
D
B
C
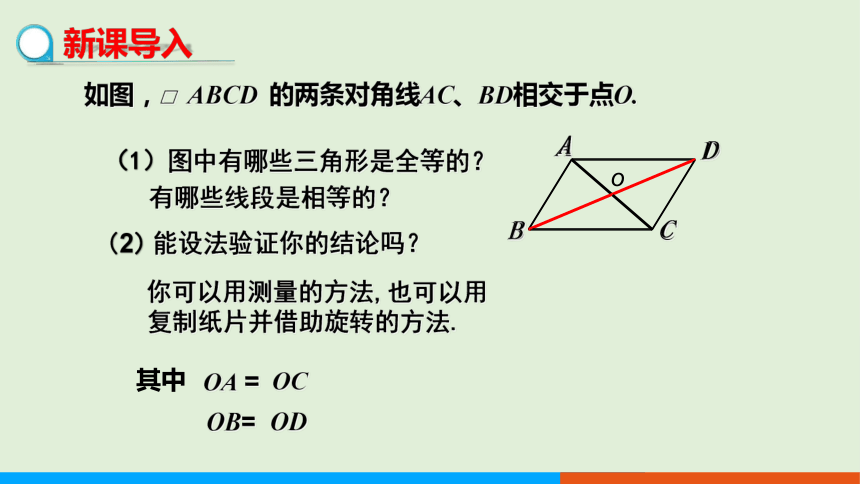
如图,□ ABCD 的两条对角线AC、BD相交于点O.
(1)图中有哪些三角形是全等的?
有哪些线段是相等的?
OA =
OC
OB=
OD
(2) 能设法验证你的结论吗?
你可以用测量的方法,也可以用复制纸片并借助旋转的方法.
A
D
B
C
o
其中
新课导入
由上题你又能得出平行四边形怎样的性质?
A
D
B
C
o
如图,□ ABCD 的两条对角线AC、BD相交于点O,
几何语言:
AO=OC= AC,
BO=OD= BD.
平行四边形的对角线互相平分
知识讲解
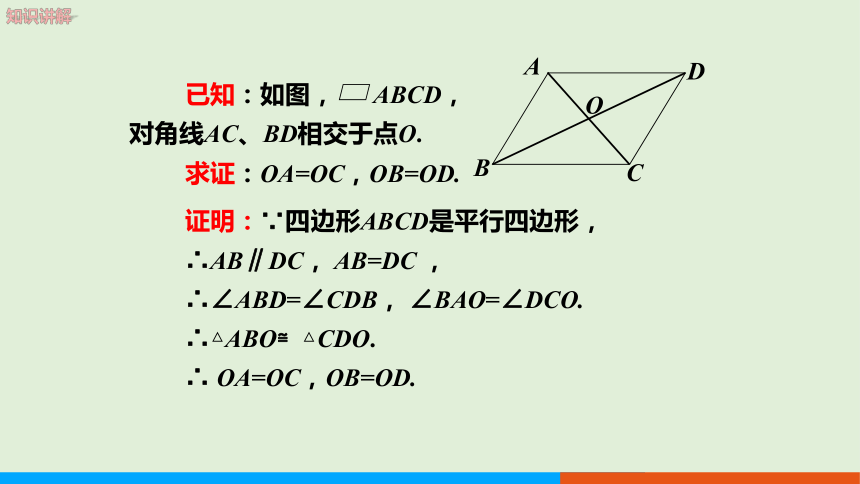
已知:如图, ABCD,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵四边形ABCD是平行四边形,
∴AB∥DC, AB=DC ,
∴∠ABD=∠CDB, ∠BAO=∠DCO.
∴△ABO≌△CDO.
∴ OA=OC,OB=OD.
A
B
C
D
O
知识讲解
例1 在 ABCD中,对角线AC与BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的 和是多少?
A
B
C
D
O
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=9.
又∵AO=OC,BO=OD,
∴AC+BD=2AO+2BO=2(AO+BO)=18.
例题讲解
D
F
A
O
B
E
C
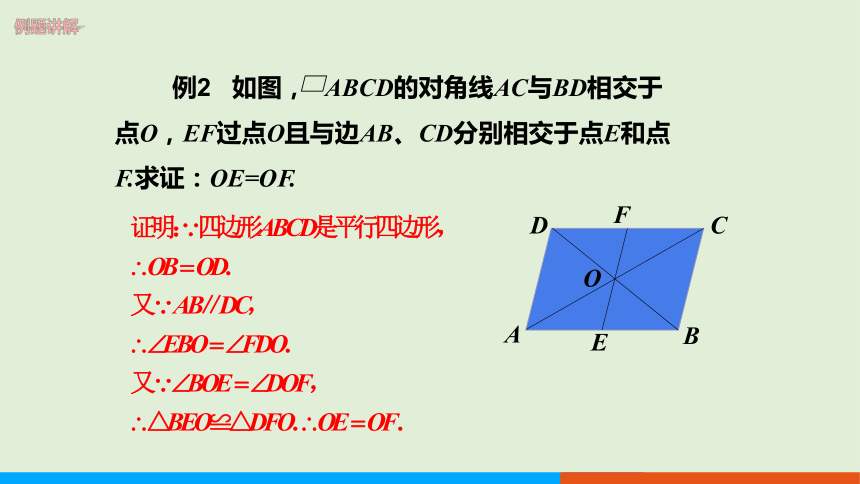
例2 如图, ABCD的对角线AC与BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点F.求证:OE=OF.
例题讲解
例3 已知 ABCD中,对角线AC,BD相交于点O,
说明= .
解:过点A作AE⊥BC于点E,过点D作DF⊥BC交BC的延长线于点F.
∵AD∥BC, AE⊥BC,DF⊥BC,
∴AE = DF(平行线之间的距离处处相等),
∴ ,
即= .
例题讲解
当堂检测
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
D
4
7
3
2. 若平行四边形的一边等于14,则它的两条对角线可能的取值分别是( )
A.8和16 B.6和16 C.2和16 D.20和22
D
3.已知: □ ABCD的对角线AC、BD相交于点
O,AC =16㎝,BD =12㎝,BC =10㎝,
则□ ABCD 的周长是_______,
□ ABCD的面积是__________。
40cm
96cm2
8
6
10
10
当堂检测
4.如图,□ ABCD的两条对角线相交于点O, 已知AB=8cm,BC=6cm, △AOB的周长是18cm,那么△AOD的周长是 .
C
B
A
D
O
16cm
当堂检测
5.如图,在□ ABCD 中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是 .
1C
B
A
D
O
当堂检测
6.在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,AC与EF互相平分吗?试说明理由.
解:AC,EF互相平分.证明如下:
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∴∠DAE=∠BEA.
又∵AE,CF分别平分∠BAD,∠BCD,
∴∠BAE=∠DAE= ,
∠BCF=∠DCF= .
∵∠BAD=∠BCD,∴∠DAE=∠BCF.
又∵∠DAE=∠BEA,
∴∠BEA=∠BCF,∴AE∥CF.
又∵AF∥CE,∴四边形AECF为平行四边形,
∴AC,EF互相平分.
当堂检测
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
第18章 平行四边形
18.1 平行四边形的性质
第18章 平行四边形
第2课时 平行四边形对角线的性质
学习目标
1.理解和掌握发现平行四边形的对角线互相平分的特征;(重点)
2.会利用平行四边形的特征进行相关的计算和说理.(难点)
A
D
B
C
如图,□ ABCD 的两条对角线AC、BD相交于点O.
(1)图中有哪些三角形是全等的?
有哪些线段是相等的?
OA =
OC
OB=
OD
(2) 能设法验证你的结论吗?
你可以用测量的方法,也可以用复制纸片并借助旋转的方法.
A
D
B
C
o
其中
新课导入
由上题你又能得出平行四边形怎样的性质?
A
D
B
C
o
如图,□ ABCD 的两条对角线AC、BD相交于点O,
几何语言:
AO=OC= AC,
BO=OD= BD.
平行四边形的对角线互相平分
知识讲解
已知:如图, ABCD,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵四边形ABCD是平行四边形,
∴AB∥DC, AB=DC ,
∴∠ABD=∠CDB, ∠BAO=∠DCO.
∴△ABO≌△CDO.
∴ OA=OC,OB=OD.
A
B
C
D
O
知识讲解
例1 在 ABCD中,对角线AC与BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC与BD的 和是多少?
A
B
C
D
O
解:在 ABCD中,
∵AB=6,AO+BO+AB=15,
∴AO+BO=9.
又∵AO=OC,BO=OD,
∴AC+BD=2AO+2BO=2(AO+BO)=18.
例题讲解
D
F
A
O
B
E
C
例2 如图, ABCD的对角线AC与BD相交于点O,EF过点O且与边AB、CD分别相交于点E和点F.求证:OE=OF.
例题讲解
例3 已知 ABCD中,对角线AC,BD相交于点O,
说明= .
解:过点A作AE⊥BC于点E,过点D作DF⊥BC交BC的延长线于点F.
∵AD∥BC, AE⊥BC,DF⊥BC,
∴AE = DF(平行线之间的距离处处相等),
∴ ,
即= .
例题讲解
当堂检测
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
D
4
7
3
2. 若平行四边形的一边等于14,则它的两条对角线可能的取值分别是( )
A.8和16 B.6和16 C.2和16 D.20和22
D
3.已知: □ ABCD的对角线AC、BD相交于点
O,AC =16㎝,BD =12㎝,BC =10㎝,
则□ ABCD 的周长是_______,
□ ABCD的面积是__________。
40cm
96cm2
8
6
10
10
当堂检测
4.如图,□ ABCD的两条对角线相交于点O, 已知AB=8cm,BC=6cm, △AOB的周长是18cm,那么△AOD的周长是 .
C
B
A
D
O
16cm
当堂检测
5.如图,在□ ABCD 中,AB=3,BC=5,对角线AC,BD相交于点O,则OA的取值范围是 .
1
B
A
D
O
当堂检测
6.在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD,AC与EF互相平分吗?试说明理由.
解:AC,EF互相平分.证明如下:
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∴∠DAE=∠BEA.
又∵AE,CF分别平分∠BAD,∠BCD,
∴∠BAE=∠DAE= ,
∠BCF=∠DCF= .
∵∠BAD=∠BCD,∴∠DAE=∠BCF.
又∵∠DAE=∠BEA,
∴∠BEA=∠BCF,∴AE∥CF.
又∵AF∥CE,∴四边形AECF为平行四边形,
∴AC,EF互相平分.
当堂检测
有两组对边分别平行的四边形
叫做
平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD 是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
课堂小结
