18.2平行四边形的判定(第1课时 利用边、角判定平行四边形) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 18.2平行四边形的判定(第1课时 利用边、角判定平行四边形) 教学课件--华师大版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:23:57 | ||
图片预览




文档简介
(共13张PPT)
第18章 平行四边形
18.2 平行四边形的判定
第18章 平行四边形
第1课时 利用边、角判定平 行四边形
学 习 目 标
1.掌握用平行四边形的定义判定一个四边形是平行四边形;(重点)
2.理解并掌握两组对边分别相等、一组对边平行且相等的四边形是平行四边形;(重点)
3.能运用这三种方法来证明一个四边形是平行四边形。(难点)
1. 平行四边形的定义是什么?
2. 平行四边形的性质有哪些?
3. 它们的逆命题是什么?
新课导入
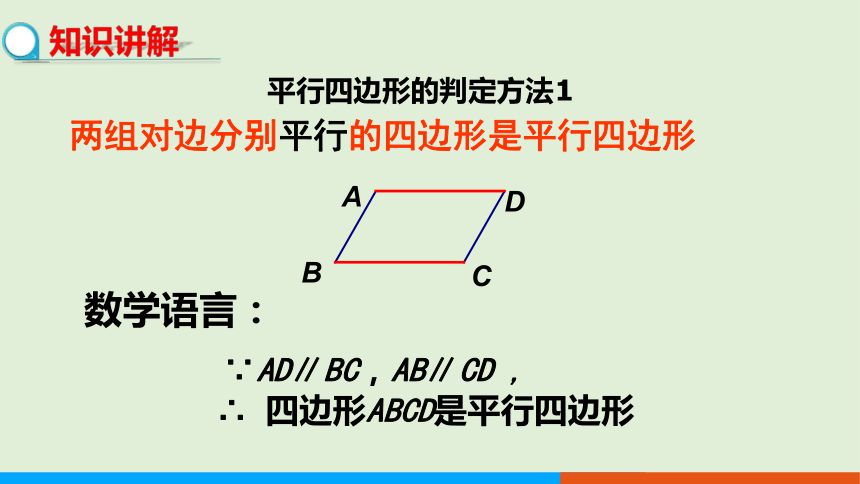
两组对边分别平行的四边形是平行四边形
∵AD∥BC,AB∥CD ,
∴ 四边形ABCD是平行四边形
数学语言:
C
B
D
A
平行四边形的判定方法1
知识讲解
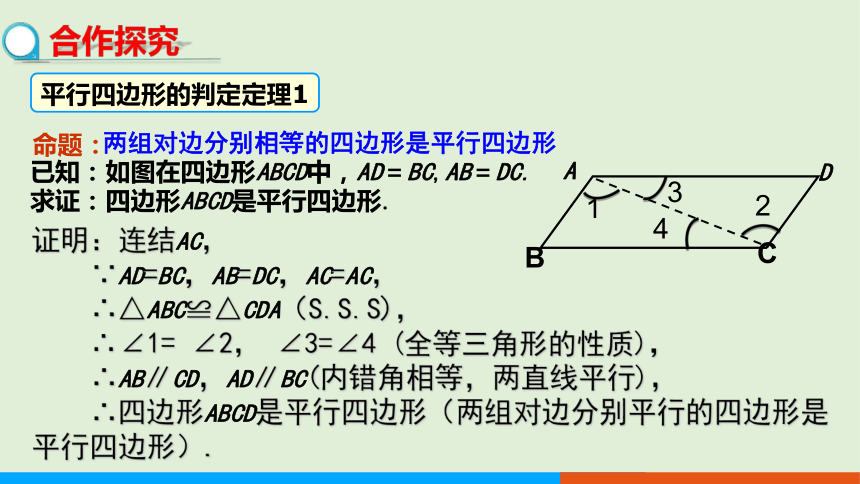
两组对边分别相等的四边形是平行四边形
已知:如图在四边形ABCD中,AD=BC,AB=DC.
求证:四边形ABCD是平行四边形.
A
C
D
1
3
2
4
B
证明:连结AC,
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌△CDA(S.S.S),
∴∠1= ∠2, ∠3=∠4 (全等三角形的性质),
∴AB∥CD,AD∥BC(内错角相等,两直线平行),
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是 平行四边形).
命题:
合作探究
平行四边形的判定定理1
几何语言:
在四边形ABCD中,
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形.
平行四边形判定定理1:两组对边分别相等的四边形是平行四边形.
C
B
D
A
合作探究
探究:一组对边平行且相等的四边形是否为平行四边形.
A
B
C
D
合作探究
平行四边形的判定定理2
已知:在四边形ABCD中,AD=BC,AD∥BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵ AD∥BC,(已知)
∴∠1=∠2.
又∵ AD=BC(已知),
AC=CA(公共边),
∴△ABC≌△CDA(SAS).
∴AB=CD,
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
1
2
合作探究
命题:
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AD//BC,AD =BC,
∴四边形ABCD是平行四边形.
几何语言:
注意:同一组对边平行且相等.
C
B
D
A
思考:一组对边平行,另一组对边相等的四边形是平行四边形吗?
合作探究
证明:
平行四边形的对边平行
∵四边形ABCD是平行四边形,
AF=CE,
例:如图,在平行四边形ABCD中,点E、F分别在对边BC和DA上,且AF=CE.
求证:四边形AECF是平行四边形.
即AF//CE.
∴四边形AECF是平行四边形.
( )
注意:遇到一题多种解题方法时,应选易避繁.
∴AD //CB , ( )
又∵
一组对边平行且相等的四边形是平行四边形
例题讲解
证明:在平行四边形ABCD中,∠A=∠C(平行四边形的对边相等).
又∵AE=CG,AH=CF(已知),
∴△AEH≌△CGF(SAS),
∴EH=GF(全等三角形的对应边相等).
在平行四边形ABCD中,AB=CD,AD=BC(平行四边形的对边相等),
∴AB﹣AE=CD﹣CG,AD﹣AH=BC﹣CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH,
∴GH=EF(全等三角形的对应边相等),
∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.
当堂检测
课堂小结
平行四边形
的判定
定义法
判定1
判定2
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
第18章 平行四边形
18.2 平行四边形的判定
第18章 平行四边形
第1课时 利用边、角判定平 行四边形
学 习 目 标
1.掌握用平行四边形的定义判定一个四边形是平行四边形;(重点)
2.理解并掌握两组对边分别相等、一组对边平行且相等的四边形是平行四边形;(重点)
3.能运用这三种方法来证明一个四边形是平行四边形。(难点)
1. 平行四边形的定义是什么?
2. 平行四边形的性质有哪些?
3. 它们的逆命题是什么?
新课导入
两组对边分别平行的四边形是平行四边形
∵AD∥BC,AB∥CD ,
∴ 四边形ABCD是平行四边形
数学语言:
C
B
D
A
平行四边形的判定方法1
知识讲解
两组对边分别相等的四边形是平行四边形
已知:如图在四边形ABCD中,AD=BC,AB=DC.
求证:四边形ABCD是平行四边形.
A
C
D
1
3
2
4
B
证明:连结AC,
∵AD=BC,AB=DC,AC=AC,
∴△ABC≌△CDA(S.S.S),
∴∠1= ∠2, ∠3=∠4 (全等三角形的性质),
∴AB∥CD,AD∥BC(内错角相等,两直线平行),
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是 平行四边形).
命题:
合作探究
平行四边形的判定定理1
几何语言:
在四边形ABCD中,
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形.
平行四边形判定定理1:两组对边分别相等的四边形是平行四边形.
C
B
D
A
合作探究
探究:一组对边平行且相等的四边形是否为平行四边形.
A
B
C
D
合作探究
平行四边形的判定定理2
已知:在四边形ABCD中,AD=BC,AD∥BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵ AD∥BC,(已知)
∴∠1=∠2.
又∵ AD=BC(已知),
AC=CA(公共边),
∴△ABC≌△CDA(SAS).
∴AB=CD,
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
1
2
合作探究
命题:
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AD//BC,AD =BC,
∴四边形ABCD是平行四边形.
几何语言:
注意:同一组对边平行且相等.
C
B
D
A
思考:一组对边平行,另一组对边相等的四边形是平行四边形吗?
合作探究
证明:
平行四边形的对边平行
∵四边形ABCD是平行四边形,
AF=CE,
例:如图,在平行四边形ABCD中,点E、F分别在对边BC和DA上,且AF=CE.
求证:四边形AECF是平行四边形.
即AF//CE.
∴四边形AECF是平行四边形.
( )
注意:遇到一题多种解题方法时,应选易避繁.
∴AD //CB , ( )
又∵
一组对边平行且相等的四边形是平行四边形
例题讲解
证明:在平行四边形ABCD中,∠A=∠C(平行四边形的对边相等).
又∵AE=CG,AH=CF(已知),
∴△AEH≌△CGF(SAS),
∴EH=GF(全等三角形的对应边相等).
在平行四边形ABCD中,AB=CD,AD=BC(平行四边形的对边相等),
∴AB﹣AE=CD﹣CG,AD﹣AH=BC﹣CF,
即BE=DG,DH=BF.
又∵在平行四边形ABCD中,∠B=∠D,
∴△BEF≌△DGH,
∴GH=EF(全等三角形的对应边相等),
∴四边形EFGH是平行四边形(两组对边分别相等的四边形是平行四边形).
如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形.
当堂检测
课堂小结
平行四边形
的判定
定义法
判定1
判定2
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
