5.4 平移 教学课件--人教版初中数学七年级下
文档属性
| 名称 | 5.4 平移 教学课件--人教版初中数学七年级下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第 五 章 相交线与平行线
第五章 相交线与平行线
5.4 平 移
学 习 目 标
1
2
理解平移的概念及决定因素.(难点)
会找出平移前后图形中对应点、对应角和对应线段.
掌握平移的性质及其运用.(重点)
3
新课导入
图片引入
观察上面几组美丽的图案,它们有什么共同的特点?能否根据每幅图中的一部分绘制出整幅图案?
这些运动有什么共同的特点?
知识讲解
★ 平移的相关概念
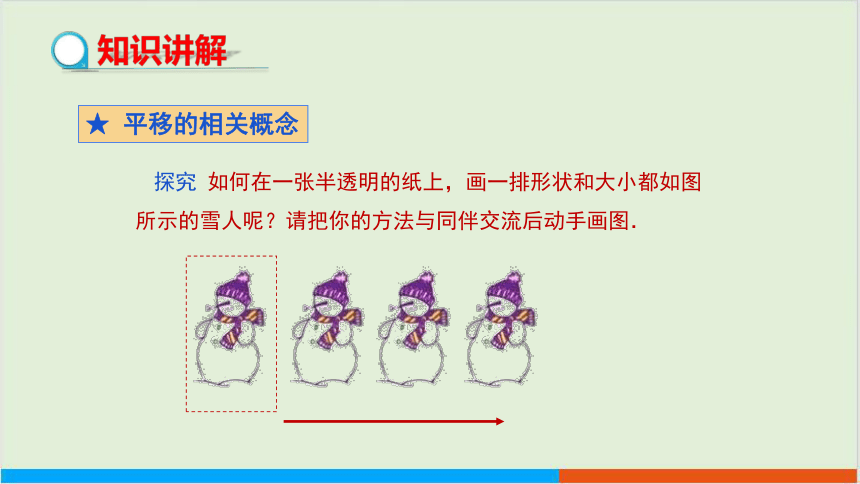
探究 如何在一张半透明的纸上,画一排形状和大小都如图所示的雪人呢?请把你的方法与同伴交流后动手画图.
思考:“雪人”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
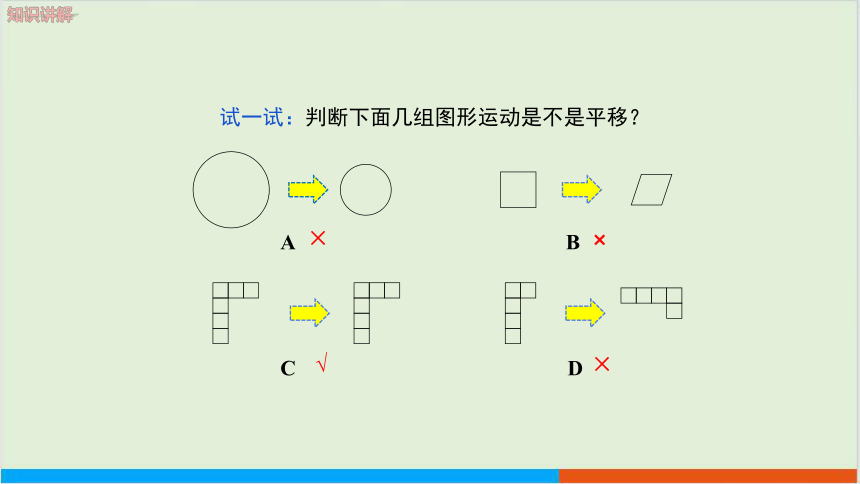
试一试:判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
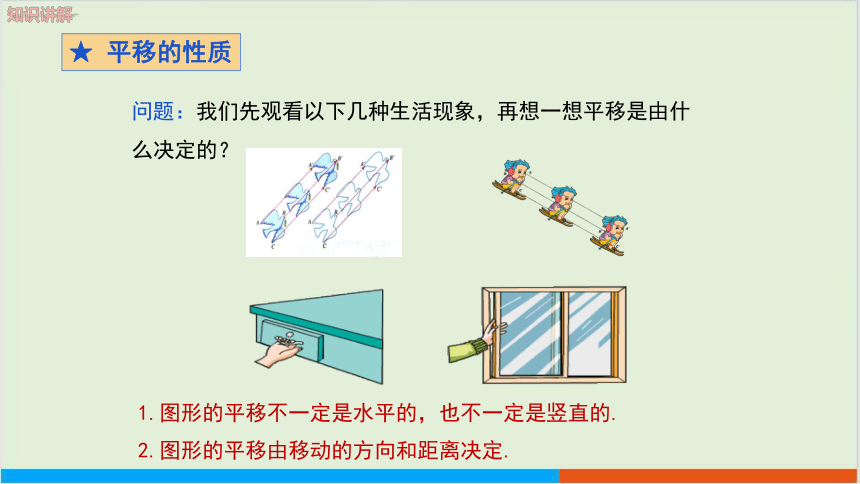
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
2.图形的平移由移动的方向和距离决定.
1.图形的平移不一定是水平的,也不一定是竖直的.
★ 平移的性质
A
B
C
D
E
F
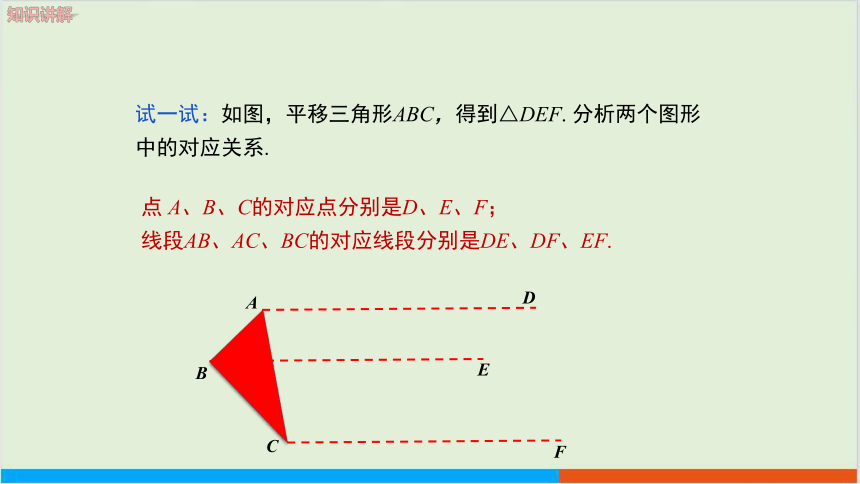
试一试:如图,平移三角形ABC,得到△DEF. 分析两个图形中的对应关系.
点 A、B、C的对应点分别是D、E、F;
线段AB、AC、BC的对应线段分别是DE、DF、EF.
思考:上面图形中AD、BE、CF都有怎样的关系?
A
B
C
D
E
F
线段AD、BE、CF平行且相等.
几何符号语言:
平移的两个图形形状和大小完全相同
A
B
C
D
E
F
∵三角形ABC平移得到三角
形DEF,
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
②对应线段平行(或在同一
直线上)且相等;
图形平移的基本性质:
③各对应点所连线段平行
(或在同一直线上)且相等;
A
B
C
D
E
F
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
F
D
A
C
B
E
对应顶点:
点D和点C,
点A和点B,
点E和点F.
AD=BC, AE=BF, DE=CF
对应边:
★ 平移作图
如图,已知线段AB,平移线段AB,使端点A 平移到A',你能作出线段AB平移后的图形A'B′吗?
⑷根据平移的性质特征如何确定B点移动后的位置B′点?
⑴要想平移整条线段,需要把握上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
B
A
A'
B'
平移一个图形的基本方法:
例2 如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:连接AA′,过点B、C两点分别做AA′的平行线l1、l2,
在l1、l2上分别截取BB′=CC′=AA′,
则B′、C′是B和C的对应点,连接A′、B′、C′即可.
C
A
B
A′
C′
B′
l1
l2
随堂训练
1.平移改变的是图形的 ( )
A. 位置 B. 大小
C. 形状 D. 位置、大小和形状
2.经过平移,对应点所连的线段 ( )
A. 平行
B. 相等
C. 平行(或在同一直线上)且相等
D. 既不平行,又不相等
A
C
3.如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
1m
1m
21m
15m
A
C
D
B
图 1
4. 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
解:长草部分的面积=(21-1)×(15-1)=280(m2).
1m
21m
15m
A
C
D
B
5.如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形.
解:长草部分的面积=(21-1)×15=300(m2).
课堂小结
关键在于按要求作出对应点;
然后,顺次连接对应点即可
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
第 五 章 相交线与平行线
第五章 相交线与平行线
5.4 平 移
学 习 目 标
1
2
理解平移的概念及决定因素.(难点)
会找出平移前后图形中对应点、对应角和对应线段.
掌握平移的性质及其运用.(重点)
3
新课导入
图片引入
观察上面几组美丽的图案,它们有什么共同的特点?能否根据每幅图中的一部分绘制出整幅图案?
这些运动有什么共同的特点?
知识讲解
★ 平移的相关概念
探究 如何在一张半透明的纸上,画一排形状和大小都如图所示的雪人呢?请把你的方法与同伴交流后动手画图.
思考:“雪人”的形状、大小、位置在运动前后是否发生了变化?
形状不变,大小不变,位置改变
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
试一试:判断下面几组图形运动是不是平移?
A
C
D
B
×
×
√
×
问题:我们先观看以下几种生活现象,再想一想平移是由什么决定的?
2.图形的平移由移动的方向和距离决定.
1.图形的平移不一定是水平的,也不一定是竖直的.
★ 平移的性质
A
B
C
D
E
F
试一试:如图,平移三角形ABC,得到△DEF. 分析两个图形中的对应关系.
点 A、B、C的对应点分别是D、E、F;
线段AB、AC、BC的对应线段分别是DE、DF、EF.
思考:上面图形中AD、BE、CF都有怎样的关系?
A
B
C
D
E
F
线段AD、BE、CF平行且相等.
几何符号语言:
平移的两个图形形状和大小完全相同
A
B
C
D
E
F
∵三角形ABC平移得到三角
形DEF,
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF,
AD∥BE∥CF(或共线),
AD=BE=CF.
②对应线段平行(或在同一
直线上)且相等;
图形平移的基本性质:
③各对应点所连线段平行
(或在同一直线上)且相等;
A
B
C
D
E
F
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
F
D
A
C
B
E
对应顶点:
点D和点C,
点A和点B,
点E和点F.
AD=BC, AE=BF, DE=CF
对应边:
★ 平移作图
如图,已知线段AB,平移线段AB,使端点A 平移到A',你能作出线段AB平移后的图形A'B′吗?
⑷根据平移的性质特征如何确定B点移动后的位置B′点?
⑴要想平移整条线段,需要把握上哪些关键的点?
⑵平移的方向是什么?
⑶平移的距离是谁的长度?
①先确定被平移图形的特殊点;
②再过特殊点沿平移的方向作出平行线;
③在平行线上分别截取特殊点移动的距离,确定特殊点平移后的位置;
④连接平移后的各点成图.
B
A
A'
B'
平移一个图形的基本方法:
例2 如图,平移三角形ABC,使点A移动到点A’,画出平移后的三角形A’B’C’.
解:连接AA′,过点B、C两点分别做AA′的平行线l1、l2,
在l1、l2上分别截取BB′=CC′=AA′,
则B′、C′是B和C的对应点,连接A′、B′、C′即可.
C
A
B
A′
C′
B′
l1
l2
随堂训练
1.平移改变的是图形的 ( )
A. 位置 B. 大小
C. 形状 D. 位置、大小和形状
2.经过平移,对应点所连的线段 ( )
A. 平行
B. 相等
C. 平行(或在同一直线上)且相等
D. 既不平行,又不相等
A
C
3.如图,经过平移,四边形ABCD的顶点A移动到点A′,作出平移后的四边形.
A
B
C
D
A′
D′
C′
B′
1m
1m
21m
15m
A
C
D
B
图 1
4. 如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
解:长草部分的面积=(21-1)×(15-1)=280(m2).
1m
21m
15m
A
C
D
B
5.如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
思路点拨:平移构成规则图形.
解:长草部分的面积=(21-1)×15=300(m2).
课堂小结
关键在于按要求作出对应点;
然后,顺次连接对应点即可
平移前后图形的形状和大小,完全相同
对应线段平行(或在同一直线上)且相等
平移的概念
平移的性质
平移作图
平移
各对应点所连线段平行(或在同一直线上)且相等
