18.2平行四边形的判定(第2课时 利用对角线判定平行四边形) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 18.2平行四边形的判定(第2课时 利用对角线判定平行四边形) 教学课件--华师大版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:24:03 | ||
图片预览





文档简介
(共14张PPT)
第18章 平行四边形
18.2 平行四边形的判定
第18章 平行四边形
第2课时 利用对角线判定平行四边形
学 习 目 标
1.掌握用“对角线互相平分的四边形是平行四边形”这一判定定理;(重点)
2.会用这些定理进行有关的论证和计算。(难点)
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义:
2、两组对边相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 .
平行四边形的对角线具有什么性质?
平行四边形的对角线互相平分.
这个命题的逆命题是什么?
新课导入
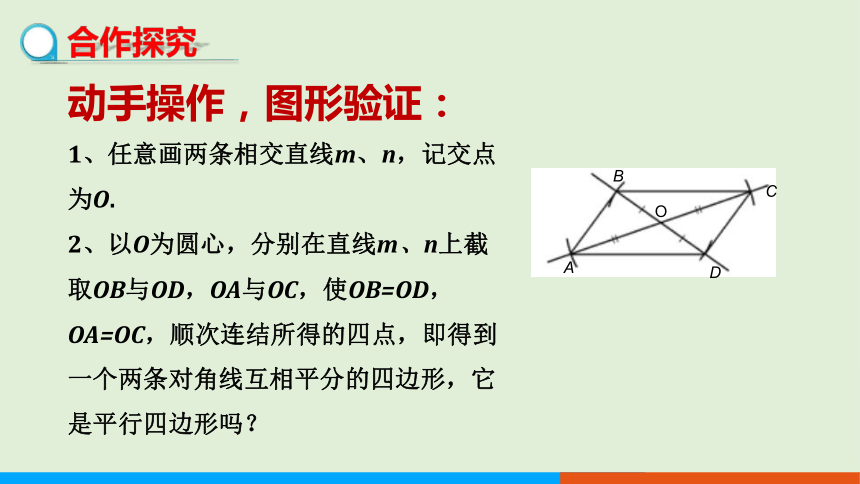
动手操作,图形验证:
1、任意画两条相交直线m、n,记交点为O.
2、以O为圆心,分别在直线m、n上截取OB与OD,OA与OC,使OB=OD,OA=OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形,它是平行四边形吗?
A
C
B
D
O
合作探究
已知:如图,在四边形ABCD中,对角线AC和BD 相交于点O,AO=CO, BO=DO.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
对角线互相平分的四边形是平行四边形.
证明:在△AOD和△COB中 ,
∵AO=CO,BO=DO,∠AOD =∠COB,
∴ △AOD≌△COB(SAS),
∴ AD=BC,∠OAD=∠OCB,∴AD∥BC.
又∵AD=BC, AD∥BC ,∴四边形ABCD是平行四边形.
求证:四边形ABCD是平行四边形.
合作探究
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
知识讲解
数学表达式:
在四边形ABCD中,
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
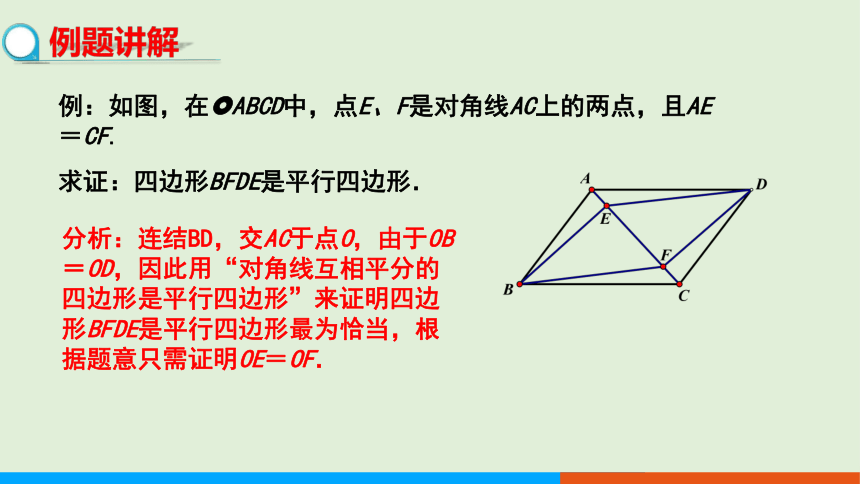
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF.
求证:四边形BFDE是平行四边形.
例题讲解
分析:连结BD,交AC于点O,由于OB=OD,因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明:连结BD,交AC于点O.
∵ 四边形ABCD是平行四边形,
∴ OB=OD, OA=OC(平行四边形对角线互相平分).
∵ AE=FC,
∴ OA-AE=OC-CF,
即 OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
例题讲解
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法2
一组对边平行且相等的四边形是平行四边形
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
当堂检测
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
当堂检测
3
当堂检测
平行四边形的判定定理3
对角线互相平分的四边形是平行四边形
平行四边形的性质与判定的综合运用
课堂小结
第18章 平行四边形
18.2 平行四边形的判定
第18章 平行四边形
第2课时 利用对角线判定平行四边形
学 习 目 标
1.掌握用“对角线互相平分的四边形是平行四边形”这一判定定理;(重点)
2.会用这些定理进行有关的论证和计算。(难点)
我们学习了哪些判定平行四边形的方法?
1、平行四边形的定义:
2、两组对边相等的四边形是平行四边形;
3、一组对边平行且相等的四边形是平行四边形 .
平行四边形的对角线具有什么性质?
平行四边形的对角线互相平分.
这个命题的逆命题是什么?
新课导入
动手操作,图形验证:
1、任意画两条相交直线m、n,记交点为O.
2、以O为圆心,分别在直线m、n上截取OB与OD,OA与OC,使OB=OD,OA=OC,顺次连结所得的四点,即得到一个两条对角线互相平分的四边形,它是平行四边形吗?
A
C
B
D
O
合作探究
已知:如图,在四边形ABCD中,对角线AC和BD 相交于点O,AO=CO, BO=DO.
分析:要证明四边形ABCD是平行四边形,可以用定义,也可以用平行四边形的两条判定方法,请你选择一种方法完成证明.
对角线互相平分的四边形是平行四边形.
证明:在△AOD和△COB中 ,
∵AO=CO,BO=DO,∠AOD =∠COB,
∴ △AOD≌△COB(SAS),
∴ AD=BC,∠OAD=∠OCB,∴AD∥BC.
又∵AD=BC, AD∥BC ,∴四边形ABCD是平行四边形.
求证:四边形ABCD是平行四边形.
合作探究
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
知识讲解
数学表达式:
在四边形ABCD中,
∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
B
O
D
A
C
例:如图,在 ABCD中,点E、F是对角线AC上的两点,且AE=CF.
求证:四边形BFDE是平行四边形.
例题讲解
分析:连结BD,交AC于点O,由于OB=OD,因此用“对角线互相平分的四边形是平行四边形”来证明四边形BFDE是平行四边形最为恰当,根据题意只需证明OE=OF.
证明:连结BD,交AC于点O.
∵ 四边形ABCD是平行四边形,
∴ OB=OD, OA=OC(平行四边形对角线互相平分).
∵ AE=FC,
∴ OA-AE=OC-CF,
即 OE=OF,
∴ 四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形).
例题讲解
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法3
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形
两组对边分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
判定方法2
一组对边平行且相等的四边形是平行四边形
∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形
平行四边形的判定方法
当堂检测
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
2.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.
B
O
D
A
C
4
5
当堂检测
3
当堂检测
平行四边形的判定定理3
对角线互相平分的四边形是平行四边形
平行四边形的性质与判定的综合运用
课堂小结
