6.1 第1课时 算术平方根 教学课件--人教版初中数学七年级下
文档属性
| 名称 | 6.1 第1课时 算术平方根 教学课件--人教版初中数学七年级下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 954.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:49 | ||
图片预览








文档简介
(共21张PPT)
第六章 实数
6.1 平方根
第 六章 实数
第1课时 算术平方根
学 习 目 标
1
2
了解算术平方根的概念,会用根号表示一个数的算术
平方根;(重点)
会求非负数的算术平方根,掌握算术平方根的非负性.
(重点、难点)
学校要举行美术作品比赛,小红想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小红算一算吗?
新课导入
面积
1
1.96
2.25
9
16
36
边长
1
1. 4
1.5
3
4
6
这个问题,实际上是已知一个正数的平方, 求这个正数.
知识讲解
算术平方根
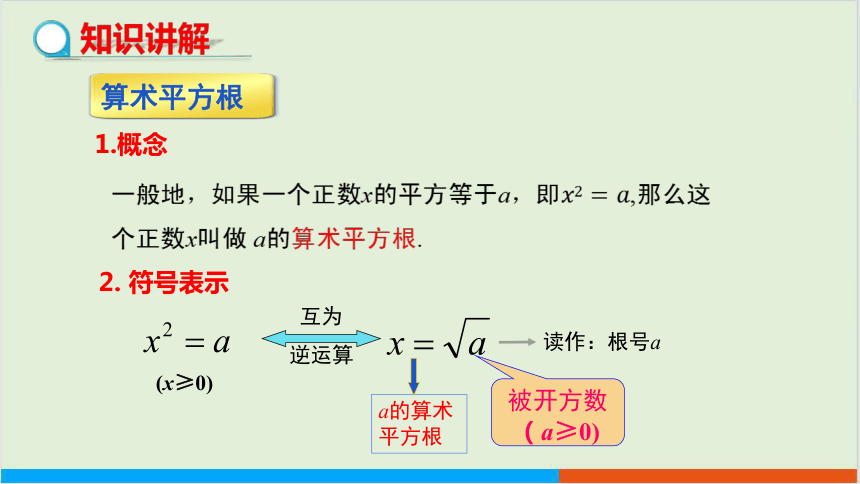
1.概念
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2. 符号表示
a的算术平方根
互为
逆运算
被开方数(a≥0)
读作:根号a
(x≥0)
求下列各数的算术平方根:
;
(1)因为,
例1
解:
所以100的算术平方根为10,
即
(2)因为,
所以 的算术平方根是
即
(3)因为
所以0.0001的算术平方根为0.01,
即
可以发现:被开方数越大,对应的算术平方根也越大.
求下列各数的算术平方根:
(1)121; (2); (3);
(4); (5).
解:(1)11; (2)3; (3)3;
(4)25; (5)
练一练
3. 算术平方根的性质
(1)一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
(2)0的算术平方有几个?
负数没有算术平方根.
(3)-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个.
判断:
(1)是的算术平方根;
(2)是 的算术平方根;
(3)的算术平方根是;
(4)是的算术平方根;
(5)是的算术平方根.
应 用
被开方数是非负数,即.
是非负数,即
即非负数的“算术平方根”是非负数,负数不存在算术平方根,即当时, 无意义.
探 究
1.可以取任何数吗?
2.是什么数?
算术平方根的双重非负性
判断:下列各式是否有意义?为什么?
有
有
有
无
例2
因为, ≥0,
解:
若|4| + =0,求的算术平方根.
所以.
又|4| + =0,
所以 , =0,
所以,
故的算术平方根为1.
规律总结
几个非负数的和为0,则每个数均为0,此时我们学过的非负数有绝对值、偶次幂及一个数的算术平方根.
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
小正方形的对角线的长是多少呢?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形。你知道这个大正方形的边长是多少吗?
解:设大正方形的边长为,则
=2.
由算术平方根的意义可知
.
例3
随堂训练
1.填空:
(1) 一个数的算术平方根是3,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是___;
和这个自然数相邻的下一个自然数是 .
(3)的算术平方根为 .
(4) 2的算术平方根为____.
9
a2
a2+1
2
2.求下列各数的算术平方根:
(1)169; (2) ; (3) 0.0001.
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.012 =0.0001,所以0.0001的算术平方根
是0.01,即
解:(1)因为132 =169,所以169的算术平方根是13,
即
3.求出下列各式的值.
解:
4.自由下落物体的高度(单位:m)与下落时间(单位:s)的关系是。如图,有一个物体从490m高的建筑物上自由落下,到达地面需要多长时间?
解:将代入公式,得
,
所以 (s).
即铁球到达地面需要100 s.
负值舍去
5. 已知:
求的值.
解:由题意得:
解得
课堂小结
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2. 符号表示
互为
逆运算
读作:根号a
(x≥0)
1. 算术平方根的概念
3. 算术平方根的性质
0的算术平方根有一个,是0;
负数没有算术平方根.
一个正数的算术平方根有1个;
第六章 实数
6.1 平方根
第 六章 实数
第1课时 算术平方根
学 习 目 标
1
2
了解算术平方根的概念,会用根号表示一个数的算术
平方根;(重点)
会求非负数的算术平方根,掌握算术平方根的非负性.
(重点、难点)
学校要举行美术作品比赛,小红想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小红算一算吗?
新课导入
面积
1
1.96
2.25
9
16
36
边长
1
1. 4
1.5
3
4
6
这个问题,实际上是已知一个正数的平方, 求这个正数.
知识讲解
算术平方根
1.概念
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2. 符号表示
a的算术平方根
互为
逆运算
被开方数(a≥0)
读作:根号a
(x≥0)
求下列各数的算术平方根:
;
(1)因为,
例1
解:
所以100的算术平方根为10,
即
(2)因为,
所以 的算术平方根是
即
(3)因为
所以0.0001的算术平方根为0.01,
即
可以发现:被开方数越大,对应的算术平方根也越大.
求下列各数的算术平方根:
(1)121; (2); (3);
(4); (5).
解:(1)11; (2)3; (3)3;
(4)25; (5)
练一练
3. 算术平方根的性质
(1)一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
(2)0的算术平方有几个?
负数没有算术平方根.
(3)-1有算术平方根吗?负数有算术平方根
一个正数的算术平方根有1个.
判断:
(1)是的算术平方根;
(2)是 的算术平方根;
(3)的算术平方根是;
(4)是的算术平方根;
(5)是的算术平方根.
应 用
被开方数是非负数,即.
是非负数,即
即非负数的“算术平方根”是非负数,负数不存在算术平方根,即当时, 无意义.
探 究
1.可以取任何数吗?
2.是什么数?
算术平方根的双重非负性
判断:下列各式是否有意义?为什么?
有
有
有
无
例2
因为, ≥0,
解:
若|4| + =0,求的算术平方根.
所以.
又|4| + =0,
所以 , =0,
所以,
故的算术平方根为1.
规律总结
几个非负数的和为0,则每个数均为0,此时我们学过的非负数有绝对值、偶次幂及一个数的算术平方根.
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?
小正方形的对角线的长是多少呢?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2的大正方形。你知道这个大正方形的边长是多少吗?
解:设大正方形的边长为,则
=2.
由算术平方根的意义可知
.
例3
随堂训练
1.填空:
(1) 一个数的算术平方根是3,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是___;
和这个自然数相邻的下一个自然数是 .
(3)的算术平方根为 .
(4) 2的算术平方根为____.
9
a2
a2+1
2
2.求下列各数的算术平方根:
(1)169; (2) ; (3) 0.0001.
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.012 =0.0001,所以0.0001的算术平方根
是0.01,即
解:(1)因为132 =169,所以169的算术平方根是13,
即
3.求出下列各式的值.
解:
4.自由下落物体的高度(单位:m)与下落时间(单位:s)的关系是。如图,有一个物体从490m高的建筑物上自由落下,到达地面需要多长时间?
解:将代入公式,得
,
所以 (s).
即铁球到达地面需要100 s.
负值舍去
5. 已知:
求的值.
解:由题意得:
解得
课堂小结
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2. 符号表示
互为
逆运算
读作:根号a
(x≥0)
1. 算术平方根的概念
3. 算术平方根的性质
0的算术平方根有一个,是0;
负数没有算术平方根.
一个正数的算术平方根有1个;
