6.1 第3课时 平方根 教学课件--人教版初中数学七年级下
文档属性
| 名称 | 6.1 第3课时 平方根 教学课件--人教版初中数学七年级下 |  | |
| 格式 | pptx | ||
| 文件大小 | 926.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:32:49 | ||
图片预览








文档简介
(共22张PPT)
第六章 实数
6.1 平方根
第 六章 实数
第3课时 平方根
学 习 目 标
1
2
了解平方根的概念,并理解平方与开平方的关系;
会求非负数的平方根(重点、难点).
温故知新
-37, 0.64, , 0, .
-37没有算术平方根.
1.什么是算术平方根?
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
8
4
(1)42= ,(-4)2= ;
(3)0.82 = ,(-0.8)2 = .
16
0.64
0.64
16
思考:反过来,如果已知一个数的平方,怎样求这个数?
;
知识讲解
1.平方根的定义及性质
思考
如果一个数的平方等于9,这个数是多少?
由于,
所以这个数是3或-3.
想一想:3和-3有什么特征?
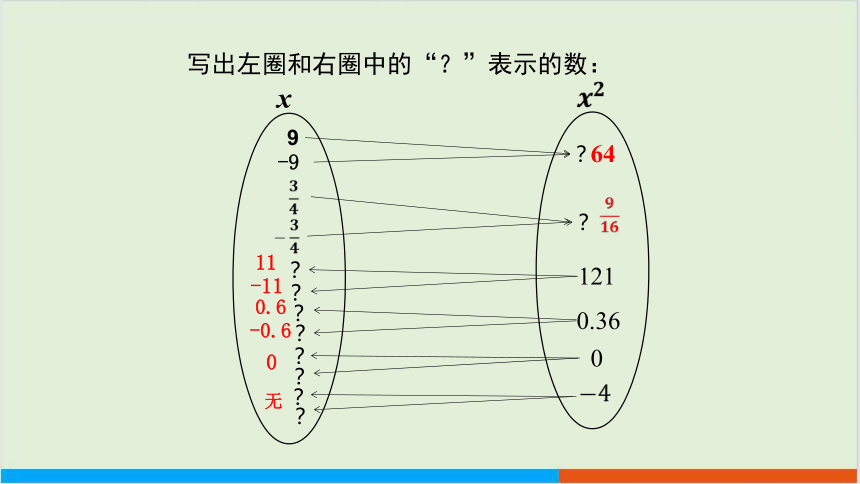
写出左圈和右圈中的“?”表示的数:
-11
11
0.6
0
无
x
9
-9
?
?
?
?
?
?
?
?
?
?
-0.6
64
121
0.36
0
平方根的概念
如果一个数的平方等于,那么这个数叫作a的平方根,
也叫作二次方根.
即:若,那么叫做的平方根.记作:
求下列各数的平方根:
(1)100; (2) (3)0.25;
(4); (5)
例1
(1)因为,所以100的平方根是
解:
(2)因为,所以的平方根是
(3)因为0.25,所以0.25的平方根是
(4) 因为49,所以的平方根是
(5) 因为25,所以的平方根是.
通过这些题目的解答,你能发现什么
(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
思考
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
平方根的性质
判断下列说法是否正确.
(1)49的平方根是7;
(2)3是9的平方根;
(3)-是的平方根;
(4)64的平方根是±8;
(5)-16的平方根是-4.
记作
a﹙a≥0﹚的平方根表示为
一个非负数a﹙a≥0﹚的平方根的表示方法:
(算术平方根)
平方根的数学符号表示
表示a的负的平方根
表示a的正的平方根
想一想
表示17的负的平方根
表示17的平方根
各表示什么意义?
一个正数的两个平方根分别是3+1和m-
5,求这个数.
解:由于一个正数的两个平方根是3+1和m-5,
则有3+1+m-5=0,即4-4=0,
解得m=1.
所以这个数为(3+1)2=(3+1)2=16.
方法归纳 一个正数有两个平方根,它们互为相反数.
例2
2.开平方
+1
-1
+2
-2
+3
-3
1
4
9
?运算
已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
求下列各式的值:
例3
(1); (2); (3).
解:
(1)因为;
(2)因为;
(3)因为
平方根与算术平方根的联系与区别
联系:
1. 平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别:
1.一个正数有两个平方根, 但只有一个算术平方根.
2. 平方根表示为,而算术平方根表示为.
随堂训练
1.下列说法正确的是______
A.0没有平方根
B.的平方根是3
C.一个数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
2.下列说法正确的是_________.
① 是9的平方根; ②的平方根是;
③49的平方根是7; ④64的算术平方根是8;
⑤平方根等于0的数是0.
①④⑤
D
3. 判断下列说法是否正确.
正确
(4)的平方根是8.
(1) 是 的一个平方根;
(2)是27的算术平方根;
(3)的值是±4;
正确
不正确,是 4.
不正确,是 .
4.求下列各式的值:
(1); (3)
解:(1)
(2)0.8;
(3)
课堂小结
如果一个数的平方等于,那么这个数叫作a的平方根,也叫作二次方根.a﹙a≥0﹚的平方根表示为.
2. 平方根的性质
1. 平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
第六章 实数
6.1 平方根
第 六章 实数
第3课时 平方根
学 习 目 标
1
2
了解平方根的概念,并理解平方与开平方的关系;
会求非负数的平方根(重点、难点).
温故知新
-37, 0.64, , 0, .
-37没有算术平方根.
1.什么是算术平方根?
一般地,如果一个正数x的平方等于a,即,那么这个正数x叫做 a的算术平方根.
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
8
4
(1)42= ,(-4)2= ;
(3)0.82 = ,(-0.8)2 = .
16
0.64
0.64
16
思考:反过来,如果已知一个数的平方,怎样求这个数?
;
知识讲解
1.平方根的定义及性质
思考
如果一个数的平方等于9,这个数是多少?
由于,
所以这个数是3或-3.
想一想:3和-3有什么特征?
写出左圈和右圈中的“?”表示的数:
-11
11
0.6
0
无
x
9
-9
?
?
?
?
?
?
?
?
?
?
-0.6
64
121
0.36
0
平方根的概念
如果一个数的平方等于,那么这个数叫作a的平方根,
也叫作二次方根.
即:若,那么叫做的平方根.记作:
求下列各数的平方根:
(1)100; (2) (3)0.25;
(4); (5)
例1
(1)因为,所以100的平方根是
解:
(2)因为,所以的平方根是
(3)因为0.25,所以0.25的平方根是
(4) 因为49,所以的平方根是
(5) 因为25,所以的平方根是.
通过这些题目的解答,你能发现什么
(1)正数有几个平方根?
(2)0有几个平方根?
(3)负数呢?
有没有一个数的平方是负数?
思考
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
平方根的性质
判断下列说法是否正确.
(1)49的平方根是7;
(2)3是9的平方根;
(3)-是的平方根;
(4)64的平方根是±8;
(5)-16的平方根是-4.
记作
a﹙a≥0﹚的平方根表示为
一个非负数a﹙a≥0﹚的平方根的表示方法:
(算术平方根)
平方根的数学符号表示
表示a的负的平方根
表示a的正的平方根
想一想
表示17的负的平方根
表示17的平方根
各表示什么意义?
一个正数的两个平方根分别是3+1和m-
5,求这个数.
解:由于一个正数的两个平方根是3+1和m-5,
则有3+1+m-5=0,即4-4=0,
解得m=1.
所以这个数为(3+1)2=(3+1)2=16.
方法归纳 一个正数有两个平方根,它们互为相反数.
例2
2.开平方
+1
-1
+2
-2
+3
-3
1
4
9
?运算
已知一个数的平方,求这个数的运算是什么?
求一个数的平方根的运算叫作开平方.
求下列各式的值:
例3
(1); (2); (3).
解:
(1)因为;
(2)因为;
(3)因为
平方根与算术平方根的联系与区别
联系:
1. 平方根包含算术平方根,算术平方根是平方根的一种.
2.只有非负数才有平方根和算术平方根.
3. 0的平方根是0,算术平方根也是0.
区别:
1.一个正数有两个平方根, 但只有一个算术平方根.
2. 平方根表示为,而算术平方根表示为.
随堂训练
1.下列说法正确的是______
A.0没有平方根
B.的平方根是3
C.一个数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
2.下列说法正确的是_________.
① 是9的平方根; ②的平方根是;
③49的平方根是7; ④64的算术平方根是8;
⑤平方根等于0的数是0.
①④⑤
D
3. 判断下列说法是否正确.
正确
(4)的平方根是8.
(1) 是 的一个平方根;
(2)是27的算术平方根;
(3)的值是±4;
正确
不正确,是 4.
不正确,是 .
4.求下列各式的值:
(1); (3)
解:(1)
(2)0.8;
(3)
课堂小结
如果一个数的平方等于,那么这个数叫作a的平方根,也叫作二次方根.a﹙a≥0﹚的平方根表示为.
2. 平方根的性质
1. 平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
