6.3 第1课时 实数 教学课件--人教版初中数学七年级下
文档属性
| 名称 | 6.3 第1课时 实数 教学课件--人教版初中数学七年级下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第六章 实数
6.3 实数
第 六章 实数
第1课时 实数
学 习 目 标
1
2
了解实数的意义,并能将实数按要求进行准确的分类;
了解实数和数轴上的点一一对应,能用数轴上的点
表示无理数;(难点)
熟练掌握实数大小的比较方法.(重点)
3
知识讲解
1.实数的概念和分类
探究
我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?
可以
(2)由此你可以得到什么结论?
任何一个有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数或无限循环小数也都是有理数.
思考2:除了有限小数和无限循环小数,还有什么其他类
型的小数吗?
无限不循环小数
叫做无理数
思考: 是无理数吗?2.020 020 002 000 02是无
理数吗?
2.02002000200002
它们都是无限不循环小数,是无理数
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
练一练
,
(相邻两个3之间7的个数逐渐加1)
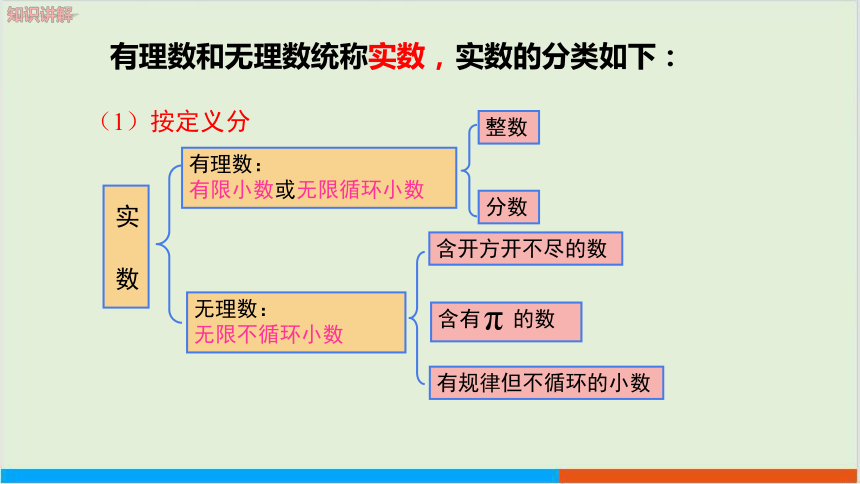
有理数和无理数统称实数,
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
实数的分类如下:
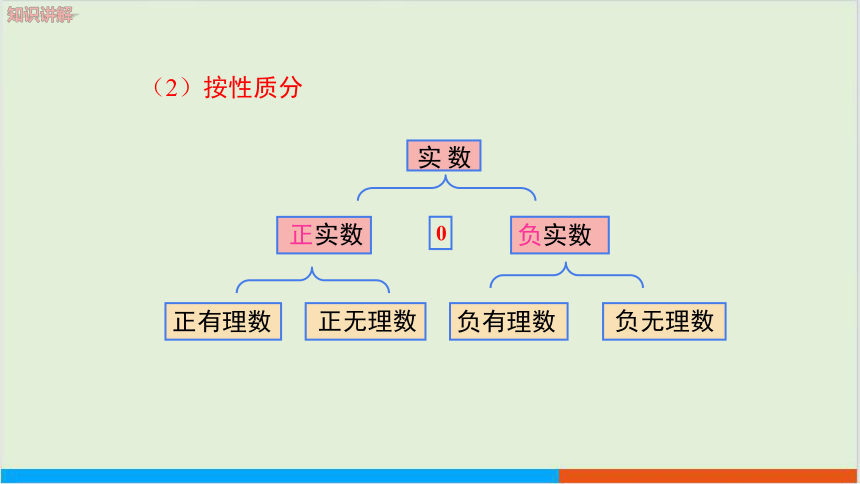
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
判断:
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
×
×
×
例1
无理数:
有理数:
负实数:
正实数:
将下列各数分别填入下列相应的括号内:
●
2.实数与数轴上的点
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
直径为1的圆
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为,从而说明边长为1的小正方形的对角线为 .
0
1
2
4
3
每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
★实数和数轴上的点是一一对应的.
如图所示,数轴上A,B两点表示的数分别为
和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴ A,B两点之间表示整数的点共有4个.
C
例2
3.实数的大小比较
与有理数一样,实数也可以比较大小:
同样的,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
-2 -1 0 1 2 3
在数轴上表示下列各点,比较它们的大小,并用连接它们.
1
-2
例3
-2<
随堂训练
1.下列说法正确的是( )
A.a一定是正实数 B. 是有理数
C.是有理数 D.数轴上任一点都对应一个有理数
B
2.估计 位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
3.把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)分数集合:
(5)正实数数集合:
(6)负实数集合:
(7) 实数集合:
,
4. 如图,数轴上A、B两点表示的数分别是和,点B关于点A的对称点为C,求点C所表示的实数.
∴点C所表示的实数为.
解:
∵数轴上A、B两点表示的数分别为和,
∴点B到点A的距离为.
∴点C到点A的距离也为.
设点C表示的实数为,则点A到点C的距离为,
∴,∴.
课堂小结
无限不循环小数叫做无理数;有理数与无理数统称实数.
2. 实数的分类
1. 无理数及实数的概念
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
3.常见的一些无理数:
(1)含的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
第六章 实数
6.3 实数
第 六章 实数
第1课时 实数
学 习 目 标
1
2
了解实数的意义,并能将实数按要求进行准确的分类;
了解实数和数轴上的点一一对应,能用数轴上的点
表示无理数;(难点)
熟练掌握实数大小的比较方法.(重点)
3
知识讲解
1.实数的概念和分类
探究
我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?
可以
(2)由此你可以得到什么结论?
任何一个有理数都可以写成有限小数或无限循环小数;
反过来,任何有限小数或无限循环小数也都是有理数.
思考2:除了有限小数和无限循环小数,还有什么其他类
型的小数吗?
无限不循环小数
叫做无理数
思考: 是无理数吗?2.020 020 002 000 02是无
理数吗?
2.02002000200002
它们都是无限不循环小数,是无理数
常见的一些无理数:
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
练一练
,
(相邻两个3之间7的个数逐渐加1)
有理数和无理数统称实数,
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
实数的分类如下:
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
判断:
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
×
×
×
例1
无理数:
有理数:
负实数:
正实数:
将下列各数分别填入下列相应的括号内:
●
2.实数与数轴上的点
每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢?
你能在数轴上找到表示 这样的无理数的点吗?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
直径为1的圆
1
1
1
1
把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为,从而说明边长为1的小正方形的对角线为 .
0
1
2
4
3
每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
★实数和数轴上的点是一一对应的.
如图所示,数轴上A,B两点表示的数分别为
和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵≈1.414,∴ 和5.1之间的整数有2,3,4,5, ∴ A,B两点之间表示整数的点共有4个.
C
例2
3.实数的大小比较
与有理数一样,实数也可以比较大小:
同样的,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
-2 -1 0 1 2 3
在数轴上表示下列各点,比较它们的大小,并用连接它们.
1
-2
例3
-2<
随堂训练
1.下列说法正确的是( )
A.a一定是正实数 B. 是有理数
C.是有理数 D.数轴上任一点都对应一个有理数
B
2.估计 位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
3.把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)整数集合:
(4)分数集合:
(5)正实数数集合:
(6)负实数集合:
(7) 实数集合:
,
4. 如图,数轴上A、B两点表示的数分别是和,点B关于点A的对称点为C,求点C所表示的实数.
∴点C所表示的实数为.
解:
∵数轴上A、B两点表示的数分别为和,
∴点B到点A的距离为.
∴点C到点A的距离也为.
设点C表示的实数为,则点A到点C的距离为,
∴,∴.
课堂小结
无限不循环小数叫做无理数;有理数与无理数统称实数.
2. 实数的分类
1. 无理数及实数的概念
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
负实数
正实数
数实
正有理数
负有理数
(2)按性质分
0
正无理数
负无理数
3.常见的一些无理数:
(1)含的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001
