19.1矩形(第2课时 矩形的判定) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 19.1矩形(第2课时 矩形的判定) 教学课件--华师大版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第19章 矩形、菱形与正方形
19.1 矩形
第19章 矩形、菱形与正方形
第2课时 矩形的判定
学 习 目 标
1.掌握矩形常见的两种识别方法.(重点)
2.学会利用矩形的判定进行简单的证明.(难点)
小明利用周末的时间,为自己做了一个相框,你能帮助小明检验一下他所做的相框是矩形吗?
矩形有哪些性质?
矩形的对边平行且相等.
矩形的四个角为直角.
矩形的对角线互相平分且相等.
矩形既是中心对称图形又是轴对称图形.
新课导入
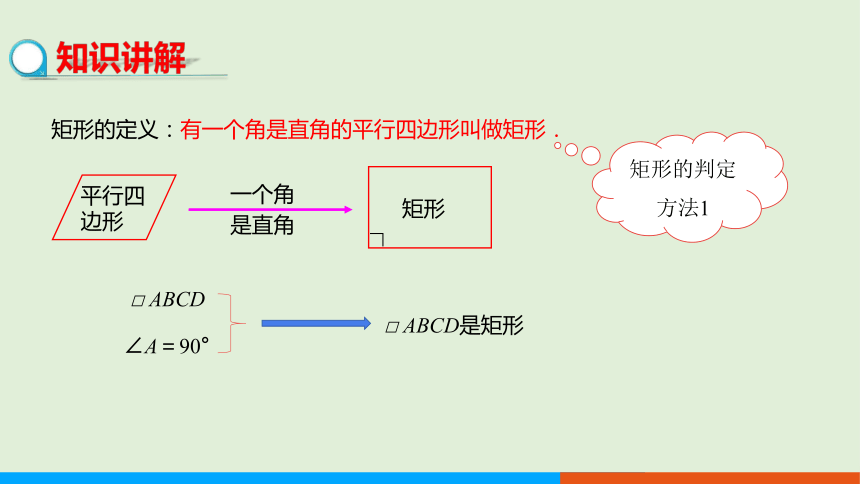
平行四
边形
一个角
是直角
∟
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形.
□ ABCD
∠A=90°
□ ABCD是矩形
矩形的判定方法1
知识讲解
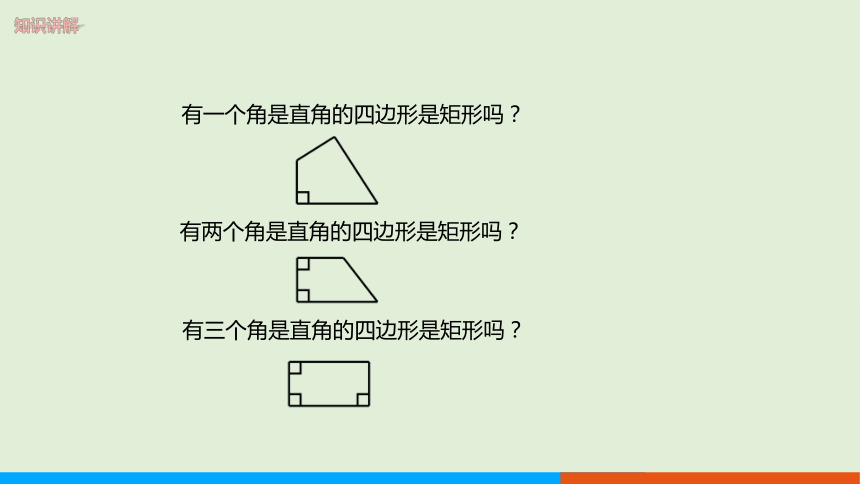
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
知识讲解
1、任意作两条互相垂直的线段AB、AD;
2、过点B作垂直于AB的直线l;
3、过点D作垂直于AD的直线m,交l于点C,即得一个三个角都是直角的四边形ABCD.
四边形ABCD是矩形吗?
知识讲解
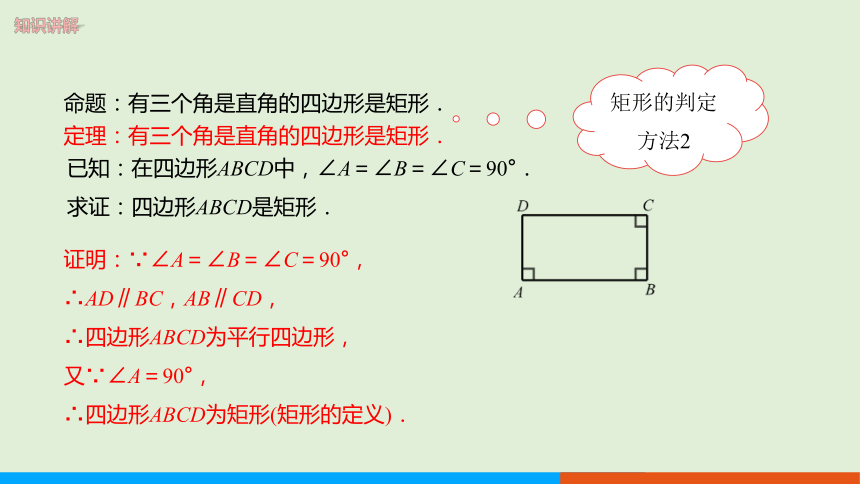
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形,
又∵∠A=90°,
∴四边形ABCD为矩形(矩形的定义).
命题:有三个角是直角的四边形是矩形.
定理:有三个角是直角的四边形是矩形.
矩形的判定方法2
知识讲解
矩形的判定定理1:有三个角是直角的四边形是矩形.
几何语言:
在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
知识讲解
由矩形的性质“矩形的对角线相等”我们可以猜想:
“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩形”.
这个猜想成立吗?
知识讲解
1、任意作两条相交的直线,交点记为O;
2、以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA、OB、OC、OD;
3、顺次连结所得的四点,即得一个对角线相等的平行四边形ABCD.
四边形ABCD是矩形吗?
知识讲解
已知:四边形ABCD是平行四边形,AC=BD.
求证:四边形ABCD是矩形.
命题:对角线相等的平行四边形是矩形.
证明:在□ ABCD中, AB=DC,BD=CA,AD=DA,
∴△BAD≌△CDA.
∴∠BAD=∠CDA.
∵AB∥CD,
∴∠BAD +∠CDA=180°,
∴∠BAD=90°,
∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形).
定理:对角线相等的平行四边形是矩形.
矩形的判定方法3
知识讲解
矩形的判定定理2:对角线相等的平行四边形是矩形.
□ ABCD
AC = BD
□ ABCD是矩形
对角线互相平分且相等的四边形是矩形吗?为什么?
四边形ABCD是矩形
结论:对角线互相平分且相等的四边形是矩形.
知识讲解
你能帮助小明检验一下他所做的相框是矩形吗?用什么方法?为什么?
1、测量相框的对角线是否相等来判断所做的相框是否是矩形.
因为对角线相等的平行四边形是矩形.
2、测量相框的三个内角是否是直角来判断所做的相框是否是矩形.
因为有三个角是直角的四边形是矩形.
知识讲解
例4 如图,O是矩形ABCD的对角线AC与BD的交点,E,F,G,H分别是AO,BO,CO,DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
分析:根据已知条件,我们可以先证明四边形EFGH是平行四边形,再证明对角线EG和FH相等,即可得证.
例题讲解
证明: ∵四边形ABCD是矩形,
∴AO=BO=CO=DO .
∵AE=BF =CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形 .
∵EO+OG=OF+OH,即EG=FH,
∴四边形EFGH是矩形 (对角线相等的平行四边形是矩形).
例题讲解
例5 如图,四边形ABCD是由两个全等正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
分析:由已知条件,可知BN⊥AD,DM⊥BC,因此,在四边形BMDN中,已有两个角是直角,只需再证明另一个角是直角即可得到它是一个矩形.
例题讲解
证明:∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,∠BDM=30°,
∴∠DNB=∠DMB=90°,
∴∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
例题讲解
例6 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.
求证:四边形ADCE是矩形.
分析:根据已知条件AB=AC,我们可以先通过证明四边形ABDE是平行四边形,得到DE=AB=AC,因此可以利用“对角线相等的平行四边形是矩形”这一判定定理证明四边形ADCE是矩形.
例题讲解
证明:∵AB=AC,AD⊥BC,∴∠B=∠ACB,BD=DC,
又∵AE是△ABC的外角∠CAF的平分线,
∴∠1= ∠CAF= (∠B+∠ACB)=∠B,
∴AE∥BC.
又∵AB∥DE,∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,
∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形(对角线相等的平行四边形是矩形).
例题讲解
1.下列条件中,不能判定四边形ABCD为矩形的是( )
A.AB∥CD,AB=CD,AC=BD
B.∠A=∠B=∠D=90°
C.AB=BC,AD=CD,且∠C=90°
D.AB=CD,AD=BC,∠A=90°
2.已知点A、B、C、D在同一平面内,有6个条件:①AB∥CD,②AB=CD,③BC∥AD,④BC=AD,⑤AC=BD,⑥∠A=90°.从这6个条件中选出(直接填写序号)____个,能使四边形ABCD是矩形.
C
当堂检测
答案不唯一,只要写出一组即可 ①②⑥,①③⑥,①②⑤,①③⑤,②④⑤,②④⑥.
3.已知:如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC.求证:四边形EBCF是矩形.
证明:∵AE=AF,∠EAB=∠FAC,AB=AC,
∴△AEB≌△AFC.
∴EB=FC,∠ABE=∠ACF.
又∵AB=AC,∴∠ABC=∠ACB.
∴∠EBC=∠FCB.
∵EB=FC,EF=BC,
∴四边形EBCF是平行四边形.
∴EB∥FC,∴∠EBC+∠FCB=190°.
∴∠EBC=∠FCB=90°,∴四边形EBCF是矩形.
当堂检测
课堂小结
矩形的判定
定义法
判定1
判定2
有一个角是直角的平行四边形叫做矩形.
有三个角是直角的四边形是矩形.
对角线相等的平行四边形是矩形.
第19章 矩形、菱形与正方形
19.1 矩形
第19章 矩形、菱形与正方形
第2课时 矩形的判定
学 习 目 标
1.掌握矩形常见的两种识别方法.(重点)
2.学会利用矩形的判定进行简单的证明.(难点)
小明利用周末的时间,为自己做了一个相框,你能帮助小明检验一下他所做的相框是矩形吗?
矩形有哪些性质?
矩形的对边平行且相等.
矩形的四个角为直角.
矩形的对角线互相平分且相等.
矩形既是中心对称图形又是轴对称图形.
新课导入
平行四
边形
一个角
是直角
∟
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形.
□ ABCD
∠A=90°
□ ABCD是矩形
矩形的判定方法1
知识讲解
有一个角是直角的四边形是矩形吗?
有两个角是直角的四边形是矩形吗?
有三个角是直角的四边形是矩形吗?
知识讲解
1、任意作两条互相垂直的线段AB、AD;
2、过点B作垂直于AB的直线l;
3、过点D作垂直于AD的直线m,交l于点C,即得一个三个角都是直角的四边形ABCD.
四边形ABCD是矩形吗?
知识讲解
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:∵∠A=∠B=∠C=90°,
∴AD∥BC,AB∥CD,
∴四边形ABCD为平行四边形,
又∵∠A=90°,
∴四边形ABCD为矩形(矩形的定义).
命题:有三个角是直角的四边形是矩形.
定理:有三个角是直角的四边形是矩形.
矩形的判定方法2
知识讲解
矩形的判定定理1:有三个角是直角的四边形是矩形.
几何语言:
在四边形ABCD中,
∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.
知识讲解
由矩形的性质“矩形的对角线相等”我们可以猜想:
“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩形”.
这个猜想成立吗?
知识讲解
1、任意作两条相交的直线,交点记为O;
2、以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA、OB、OC、OD;
3、顺次连结所得的四点,即得一个对角线相等的平行四边形ABCD.
四边形ABCD是矩形吗?
知识讲解
已知:四边形ABCD是平行四边形,AC=BD.
求证:四边形ABCD是矩形.
命题:对角线相等的平行四边形是矩形.
证明:在□ ABCD中, AB=DC,BD=CA,AD=DA,
∴△BAD≌△CDA.
∴∠BAD=∠CDA.
∵AB∥CD,
∴∠BAD +∠CDA=180°,
∴∠BAD=90°,
∴四边形ABCD是矩形(有一个内角是直角的平行四边形是矩形).
定理:对角线相等的平行四边形是矩形.
矩形的判定方法3
知识讲解
矩形的判定定理2:对角线相等的平行四边形是矩形.
□ ABCD
AC = BD
□ ABCD是矩形
对角线互相平分且相等的四边形是矩形吗?为什么?
四边形ABCD是矩形
结论:对角线互相平分且相等的四边形是矩形.
知识讲解
你能帮助小明检验一下他所做的相框是矩形吗?用什么方法?为什么?
1、测量相框的对角线是否相等来判断所做的相框是否是矩形.
因为对角线相等的平行四边形是矩形.
2、测量相框的三个内角是否是直角来判断所做的相框是否是矩形.
因为有三个角是直角的四边形是矩形.
知识讲解
例4 如图,O是矩形ABCD的对角线AC与BD的交点,E,F,G,H分别是AO,BO,CO,DO上的一点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
分析:根据已知条件,我们可以先证明四边形EFGH是平行四边形,再证明对角线EG和FH相等,即可得证.
例题讲解
证明: ∵四边形ABCD是矩形,
∴AO=BO=CO=DO .
∵AE=BF =CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形 .
∵EO+OG=OF+OH,即EG=FH,
∴四边形EFGH是矩形 (对角线相等的平行四边形是矩形).
例题讲解
例5 如图,四边形ABCD是由两个全等正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.
求证:四边形BMDN是矩形.
分析:由已知条件,可知BN⊥AD,DM⊥BC,因此,在四边形BMDN中,已有两个角是直角,只需再证明另一个角是直角即可得到它是一个矩形.
例题讲解
证明:∵△ABD和△BCD是全等的正三角形,
∴∠ADB=∠CDB=60°.
又∵M、N分别为BC、AD的中点,
∴BN⊥AD,DM⊥BC,∠BDM=30°,
∴∠DNB=∠DMB=90°,
∴∠MDN=∠ADB+∠BDM=90°,
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
例题讲解
例6 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.
求证:四边形ADCE是矩形.
分析:根据已知条件AB=AC,我们可以先通过证明四边形ABDE是平行四边形,得到DE=AB=AC,因此可以利用“对角线相等的平行四边形是矩形”这一判定定理证明四边形ADCE是矩形.
例题讲解
证明:∵AB=AC,AD⊥BC,∴∠B=∠ACB,BD=DC,
又∵AE是△ABC的外角∠CAF的平分线,
∴∠1= ∠CAF= (∠B+∠ACB)=∠B,
∴AE∥BC.
又∵AB∥DE,∴四边形ABDE是平行四边形,
∴AE=BD,AB=DE,
∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形(对角线相等的平行四边形是矩形).
例题讲解
1.下列条件中,不能判定四边形ABCD为矩形的是( )
A.AB∥CD,AB=CD,AC=BD
B.∠A=∠B=∠D=90°
C.AB=BC,AD=CD,且∠C=90°
D.AB=CD,AD=BC,∠A=90°
2.已知点A、B、C、D在同一平面内,有6个条件:①AB∥CD,②AB=CD,③BC∥AD,④BC=AD,⑤AC=BD,⑥∠A=90°.从这6个条件中选出(直接填写序号)____个,能使四边形ABCD是矩形.
C
当堂检测
答案不唯一,只要写出一组即可 ①②⑥,①③⑥,①②⑤,①③⑤,②④⑤,②④⑥.
3.已知:如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC.求证:四边形EBCF是矩形.
证明:∵AE=AF,∠EAB=∠FAC,AB=AC,
∴△AEB≌△AFC.
∴EB=FC,∠ABE=∠ACF.
又∵AB=AC,∴∠ABC=∠ACB.
∴∠EBC=∠FCB.
∵EB=FC,EF=BC,
∴四边形EBCF是平行四边形.
∴EB∥FC,∴∠EBC+∠FCB=190°.
∴∠EBC=∠FCB=90°,∴四边形EBCF是矩形.
当堂检测
课堂小结
矩形的判定
定义法
判定1
判定2
有一个角是直角的平行四边形叫做矩形.
有三个角是直角的四边形是矩形.
对角线相等的平行四边形是矩形.
