19.2菱形(第1课时 菱形的性质) 教学课件--华师大版数学八年级(下)
文档属性
| 名称 | 19.2菱形(第1课时 菱形的性质) 教学课件--华师大版数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第19章 矩形、菱形与正方形
19.2 菱形
第19章 矩形、菱形与正方形
第1课时 菱形的性质
学 习 目 标
1.通过折叠纸张的办法,探索菱形的性质.(重点)
2.能灵活运用菱形的性质解题.(难点)
平行四边形有哪些特征 矩形与平行四边形比较有哪些特殊的特征
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
知识回顾
观察图案,有没有你熟悉的图形
新课导入
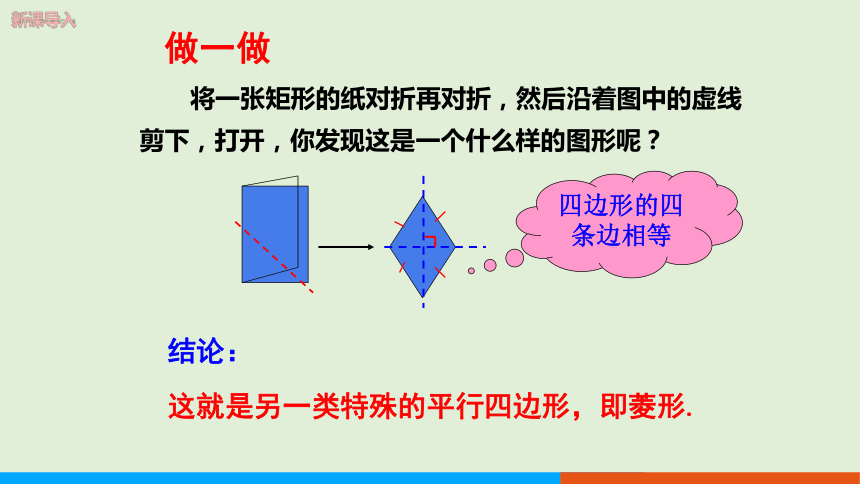
做一做
结论:
这就是另一类特殊的平行四边形,即菱形.
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
四边形的四条边相等
新课导入
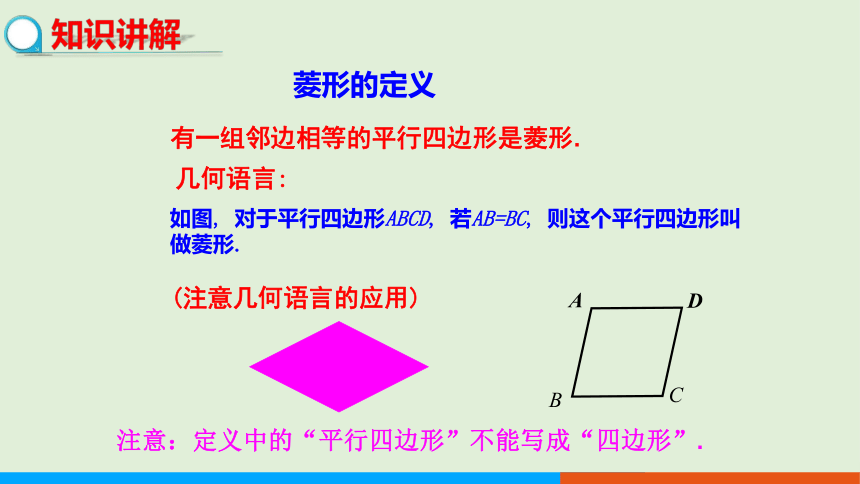
有一组邻边相等的平行四边形是菱形.
菱形的定义
几何语言:
A
B
C
D
如图, 对于平行四边形ABCD, 若AB=BC, 则这个平行四边形叫做菱形.
(注意几何语言的应用)
注意:定义中的“平行四边形”不能写成“四边形”.
知识讲解
菱形是特殊的平行四边形,它除具有一般平行四边形的性质外,还有哪些性质?
合作探究
菱形的性质
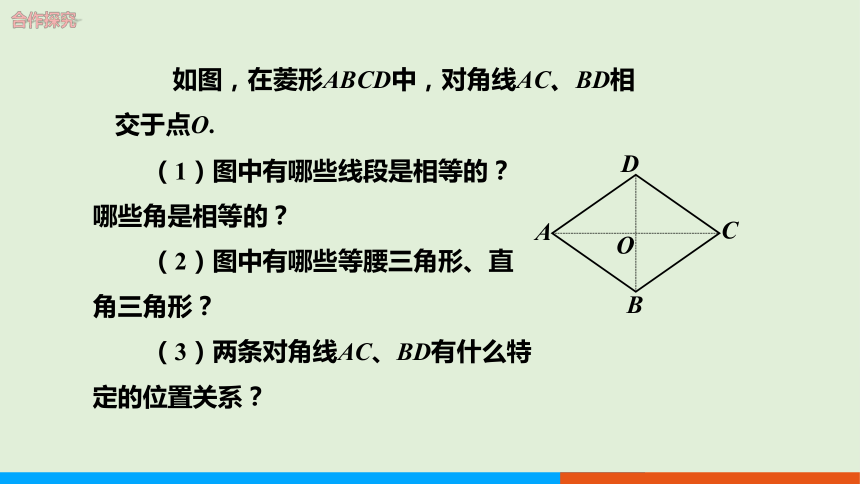
如图,在菱形ABCD中,对角线AC、BD相交于点O.
O
D
C
B
A
(1)图中有哪些线段是相等的?哪些角是相等的?
(2)图中有哪些等腰三角形、直角三角形?
(3)两条对角线AC、BD有什么特定的位置关系?
合作探究
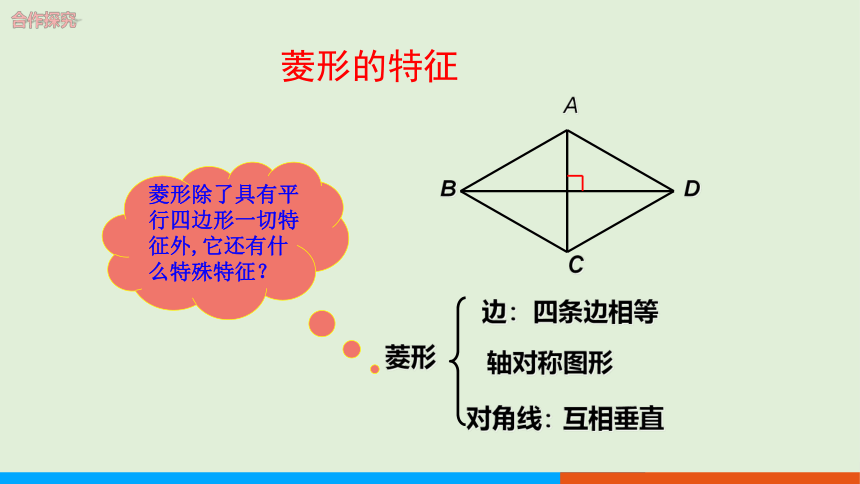
菱形除了具有平行四边形一切特征外,它还有什么特殊特征?
菱形
边:
四条边相等
对角线:
互相垂直
轴对称图形
A
B
C
D
菱形的特征
合作探究
(1)对称性:菱形是中心对称图形,对称中心是对角线的交点;也是轴对称图形,对称轴有两条,对角线所在的直线是它的对称轴.
(2)边:菱形的四条边相等.
(3)对角线:菱形的对角线互相平分且垂直.
思考:你能用逻辑推理的方法证明菱形边、对角线所特有的性质吗?试试看.
知识讲解
命题:菱形的四条边都相等
已知:如图,四边ABCD是菱形,
求证:AB=BC=CD=AD.
证明:∵四边形ABCD是菱形,
∴ AB=CD,AD=BC (平行四边形的对边相等).
∵ AB=BC,
∴ AB=BC=CD=AD.
AB=BC.
D
A
B
C
知识讲解
已知:如图,菱形ABCD 的对角线AC 和BD 相交于点O.
证明:∵四边形ABCD是菱形,
A
B
C
D
O
∴AB=AD ,BO=DO,
∴AC⊥BD(等腰三角形的“三线合一”).
求证:AC⊥BD.
命题:菱形的对角线互相垂直.
知识讲解
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形.
在菱形ABCD中,
所以∠B+∠BAD=180 (两直线平行同旁内角互补).
又因为∠BAD=2∠B,
所以∠B=60 .
在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等).
所以在△ABC中,∠BAC=∠BCA(等边对等角).
又因为∠B+∠BAC+∠BCA=180 (三角形内角和定理),
所以∠BAC=∠BCA=∠B=60 .
所以AB=BC=AC(等角对等边).
即△ABC是等边三角形.
因为AD∥BC,
例题讲解
例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.
解:在菱形ABCD中,
又在△ABC中,AB=BC,
∠BAO= ∠BAD= ×120°=60°
所以∠BCA=∠BAC=60°(等边对等角),
∠ABC=180°∠BCA∠BAC=60°,
所以△ABC为等边三角形,
故AC=AB=2(cm).
(菱形的每一条对角线平分一组对角).
A
D
C
B
O
所以AB=BC=AC(等角对等边),
例题讲解
解:在菱形ABCD中,
.
所以BD=2BO= (cm).
A
D
C
B
O
AC⊥BD(菱形的对角线互相垂直),
所以 △AOB为直角三角形.
例题讲解
例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.
例3 如图,菱形ABCD的对角线AC、BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
A
B
C
D
O
E
例题讲解
∵四边形ABCD是菱形,
解:
∴AD=DC=CB=BA(菱形的四条边相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即ΔADC和Δ ABC都为等边三角形,
∴∠ACD= ∠ACB=60°.
∴∠BCD=120°.
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____和____.
2.已知菱形的两条对角线分别是6cm和8cm,则菱形的周长和面积分别是______和_____.
60°
当堂检测
120°
20cm
24 cm2
3.如图,四边形ABCD是边长为13cm的菱形,其中对
角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
4.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm.
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
第19章 矩形、菱形与正方形
19.2 菱形
第19章 矩形、菱形与正方形
第1课时 菱形的性质
学 习 目 标
1.通过折叠纸张的办法,探索菱形的性质.(重点)
2.能灵活运用菱形的性质解题.(难点)
平行四边形有哪些特征 矩形与平行四边形比较有哪些特殊的特征
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
知识回顾
观察图案,有没有你熟悉的图形
新课导入
做一做
结论:
这就是另一类特殊的平行四边形,即菱形.
将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
四边形的四条边相等
新课导入
有一组邻边相等的平行四边形是菱形.
菱形的定义
几何语言:
A
B
C
D
如图, 对于平行四边形ABCD, 若AB=BC, 则这个平行四边形叫做菱形.
(注意几何语言的应用)
注意:定义中的“平行四边形”不能写成“四边形”.
知识讲解
菱形是特殊的平行四边形,它除具有一般平行四边形的性质外,还有哪些性质?
合作探究
菱形的性质
如图,在菱形ABCD中,对角线AC、BD相交于点O.
O
D
C
B
A
(1)图中有哪些线段是相等的?哪些角是相等的?
(2)图中有哪些等腰三角形、直角三角形?
(3)两条对角线AC、BD有什么特定的位置关系?
合作探究
菱形除了具有平行四边形一切特征外,它还有什么特殊特征?
菱形
边:
四条边相等
对角线:
互相垂直
轴对称图形
A
B
C
D
菱形的特征
合作探究
(1)对称性:菱形是中心对称图形,对称中心是对角线的交点;也是轴对称图形,对称轴有两条,对角线所在的直线是它的对称轴.
(2)边:菱形的四条边相等.
(3)对角线:菱形的对角线互相平分且垂直.
思考:你能用逻辑推理的方法证明菱形边、对角线所特有的性质吗?试试看.
知识讲解
命题:菱形的四条边都相等
已知:如图,四边ABCD是菱形,
求证:AB=BC=CD=AD.
证明:∵四边形ABCD是菱形,
∴ AB=CD,AD=BC (平行四边形的对边相等).
∵ AB=BC,
∴ AB=BC=CD=AD.
AB=BC.
D
A
B
C
知识讲解
已知:如图,菱形ABCD 的对角线AC 和BD 相交于点O.
证明:∵四边形ABCD是菱形,
A
B
C
D
O
∴AB=AD ,BO=DO,
∴AC⊥BD(等腰三角形的“三线合一”).
求证:AC⊥BD.
命题:菱形的对角线互相垂直.
知识讲解
A
B
C
D
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的度数,并说明△ABC是等边三角形.
在菱形ABCD中,
所以∠B+∠BAD=180 (两直线平行同旁内角互补).
又因为∠BAD=2∠B,
所以∠B=60 .
在菱形ABCD中,
解:
AB=BC(菱形的四条边都相等).
所以在△ABC中,∠BAC=∠BCA(等边对等角).
又因为∠B+∠BAC+∠BCA=180 (三角形内角和定理),
所以∠BAC=∠BCA=∠B=60 .
所以AB=BC=AC(等角对等边).
即△ABC是等边三角形.
因为AD∥BC,
例题讲解
例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.
解:在菱形ABCD中,
又在△ABC中,AB=BC,
∠BAO= ∠BAD= ×120°=60°
所以∠BCA=∠BAC=60°(等边对等角),
∠ABC=180°∠BCA∠BAC=60°,
所以△ABC为等边三角形,
故AC=AB=2(cm).
(菱形的每一条对角线平分一组对角).
A
D
C
B
O
所以AB=BC=AC(等角对等边),
例题讲解
解:在菱形ABCD中,
.
所以BD=2BO= (cm).
A
D
C
B
O
AC⊥BD(菱形的对角线互相垂直),
所以 △AOB为直角三角形.
例题讲解
例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O,试求这个菱形的两条对角线AC与BD的长.
例3 如图,菱形ABCD的对角线AC、BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.
A
B
C
D
O
E
例题讲解
∵四边形ABCD是菱形,
解:
∴AD=DC=CB=BA(菱形的四条边相等).
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即ΔADC和Δ ABC都为等边三角形,
∴∠ACD= ∠ACB=60°.
∴∠BCD=120°.
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____和____.
2.已知菱形的两条对角线分别是6cm和8cm,则菱形的周长和面积分别是______和_____.
60°
当堂检测
120°
20cm
24 cm2
3.如图,四边形ABCD是边长为13cm的菱形,其中对
角线BD长10cm.
求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
解:(1)
∵四边形ABCD是菱形,
∴∠AED=90°,
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
4.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm.
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).
课堂小结
菱形的性质
菱形的性质
有关计算
边
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
角
对角线
1.两组对边平行且相等;
2.四条边相等
两组对角分别相等,邻角互补
1.两条对角线互相垂直平分;
2.每一条对角线平分一组对角
