10.2平行线的判定(第3课时) 教案--沪科版初中数学七年级(下)
文档属性
| 名称 | 10.2平行线的判定(第3课时) 教案--沪科版初中数学七年级(下) | 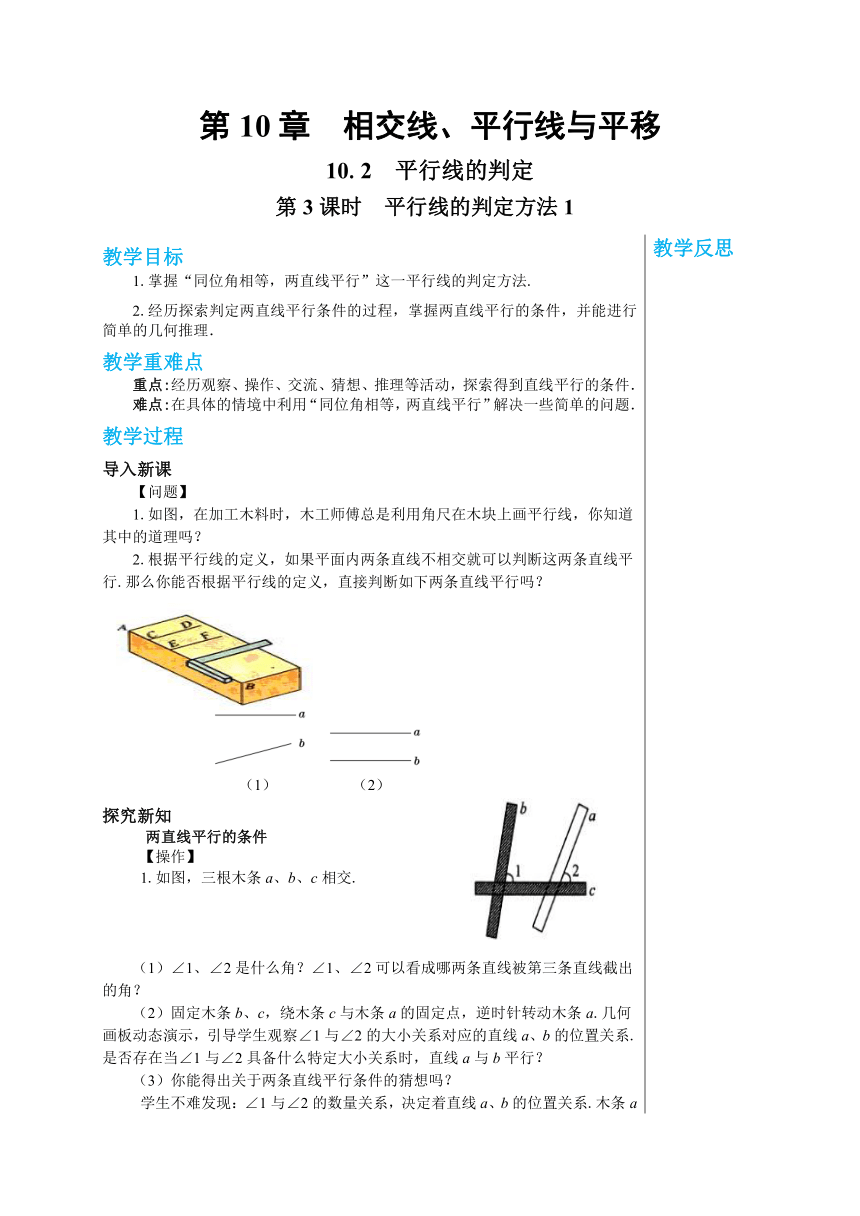 | |
| 格式 | docx | ||
| 文件大小 | 871.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:18:28 | ||
图片预览

文档简介
第10章 相交线、平行线与平移
10.2 平行线的判定
第3课时 平行线的判定方法1
教学目标 1.掌握“同位角相等,两直线平行”这一平行线的判定方法. 2.经历探索判定两直线平行条件的过程,掌握两直线平行的条件,并能进行简单的几何推理. 教学重难点 重点:经历观察、操作、交流、猜想、推理等活动,探索得到直线平行的条件. 难点:在具体的情境中利用“同位角相等,两直线平行”解决一些简单的问题. 教学过程 导入新课 【问题】 1.如图,在加工木料时,木工师傅总是利用角尺在木块上画平行线,你知道其中的道理吗? 2.根据平行线的定义,如果平面内两条直线不相交就可以判断这两条直线平行.那么你能否根据平行线的定义,直接判断如下两条直线平行吗? (1) (2) 探究新知 两直线平行的条件 【操作】 1.如图,三根木条a、b、c相交. (1)∠1、∠2是什么角?∠1、∠2可以看成哪两条直线被第三条直线截出的角? (2)固定木条b、c,绕木条c与木条a的固定点,逆时针转动木条a.几何画板动态演示,引导学生观察∠1与∠2的大小关系对应的直线a、b的位置关系.是否存在当∠1与∠2具备什么特定大小关系时,直线a与b平行? (3)你能得出关于两条直线平行条件的猜想吗? 学生不难发现:∠1与∠2的数量关系,决定着直线a、b的位置关系.木条a绕与木条c的固定点,逆时针旋转时,∠2逐渐增大,逐渐逼近∠1的大小,直线a与b不平行.当∠1与∠2相等时,直线a与b平行.继续旋转木条a,此时∠1<∠2,直线a与b不平行.由此,学生不难归纳得出猜想:直线a与b被第三条直线c所截,当同位角∠1与∠2相等时,直线a与b平行. 2.上面我们通过观察旋转的木条,归纳得出了两条直线平行的条件的猜想,这一猜想一定是正确的吗?下面我们回顾上节课利用三角尺过直线外一点画已知直线平行线这一既定事实,去进一步验证我们的猜想. 引导学生,观察讨论,得出结论. 可以看出,画直线的平行线,实际上就是过点画与∠2相等的∠1,而∠2和∠1正是直线,被直线所截得到的同位角.这一既定事实,正好验证了我们上面得出的猜想:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 【归纳】通过上面两个数学活动,学生总结归纳得出平行线的判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行. 例 (1)利用“同位角相等,两直线平行”解释引例(木匠画平行线). (2)如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由. 【解】∠3=55°,AB∥CD. ∵∠3=∠2 (对顶角相等), 而∠2=55°, ∴∠3=55°. 又∵∠1=55°, ∴∠1=∠3, ∴AB∥CD. 课堂练习 1.如图1,已知∠1=120°, ∠3=60°,判断直线a与b是否平行? 2.如图2,要使直线∥ ,需要添加一个什么条件?你有哪些添法? 图1 图2 参考答案 1.解:∵∠1=120° , 而∠1+∠2=180°, ∴∠2=60°. 又∵∠3=60°, ∴∠2=∠3, ∴a∥b. 2.∠1=∠3 ,∠2=∠4 ,∠3+∠4=180°,∠1+∠2=180°等,答案不唯一. 课堂小结 平行线的判定方法1:同位角相等,两直线平行. 布置作业 课本第126页练习第1,2题. 板书设计 10.2 平行线的判定 第3课时 平行线的判定方法1 平行线的判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 即同位角相等,两直线平行. 教学反思 教学反思 教学反思
10.2 平行线的判定
第3课时 平行线的判定方法1
教学目标 1.掌握“同位角相等,两直线平行”这一平行线的判定方法. 2.经历探索判定两直线平行条件的过程,掌握两直线平行的条件,并能进行简单的几何推理. 教学重难点 重点:经历观察、操作、交流、猜想、推理等活动,探索得到直线平行的条件. 难点:在具体的情境中利用“同位角相等,两直线平行”解决一些简单的问题. 教学过程 导入新课 【问题】 1.如图,在加工木料时,木工师傅总是利用角尺在木块上画平行线,你知道其中的道理吗? 2.根据平行线的定义,如果平面内两条直线不相交就可以判断这两条直线平行.那么你能否根据平行线的定义,直接判断如下两条直线平行吗? (1) (2) 探究新知 两直线平行的条件 【操作】 1.如图,三根木条a、b、c相交. (1)∠1、∠2是什么角?∠1、∠2可以看成哪两条直线被第三条直线截出的角? (2)固定木条b、c,绕木条c与木条a的固定点,逆时针转动木条a.几何画板动态演示,引导学生观察∠1与∠2的大小关系对应的直线a、b的位置关系.是否存在当∠1与∠2具备什么特定大小关系时,直线a与b平行? (3)你能得出关于两条直线平行条件的猜想吗? 学生不难发现:∠1与∠2的数量关系,决定着直线a、b的位置关系.木条a绕与木条c的固定点,逆时针旋转时,∠2逐渐增大,逐渐逼近∠1的大小,直线a与b不平行.当∠1与∠2相等时,直线a与b平行.继续旋转木条a,此时∠1<∠2,直线a与b不平行.由此,学生不难归纳得出猜想:直线a与b被第三条直线c所截,当同位角∠1与∠2相等时,直线a与b平行. 2.上面我们通过观察旋转的木条,归纳得出了两条直线平行的条件的猜想,这一猜想一定是正确的吗?下面我们回顾上节课利用三角尺过直线外一点画已知直线平行线这一既定事实,去进一步验证我们的猜想. 引导学生,观察讨论,得出结论. 可以看出,画直线的平行线,实际上就是过点画与∠2相等的∠1,而∠2和∠1正是直线,被直线所截得到的同位角.这一既定事实,正好验证了我们上面得出的猜想:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 【归纳】通过上面两个数学活动,学生总结归纳得出平行线的判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行. 例 (1)利用“同位角相等,两直线平行”解释引例(木匠画平行线). (2)如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由. 【解】∠3=55°,AB∥CD. ∵∠3=∠2 (对顶角相等), 而∠2=55°, ∴∠3=55°. 又∵∠1=55°, ∴∠1=∠3, ∴AB∥CD. 课堂练习 1.如图1,已知∠1=120°, ∠3=60°,判断直线a与b是否平行? 2.如图2,要使直线∥ ,需要添加一个什么条件?你有哪些添法? 图1 图2 参考答案 1.解:∵∠1=120° , 而∠1+∠2=180°, ∴∠2=60°. 又∵∠3=60°, ∴∠2=∠3, ∴a∥b. 2.∠1=∠3 ,∠2=∠4 ,∠3+∠4=180°,∠1+∠2=180°等,答案不唯一. 课堂小结 平行线的判定方法1:同位角相等,两直线平行. 布置作业 课本第126页练习第1,2题. 板书设计 10.2 平行线的判定 第3课时 平行线的判定方法1 平行线的判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 即同位角相等,两直线平行. 教学反思 教学反思 教学反思
