冀教版数学七年级下·7.1命题(第2课时)教学课件
文档属性
| 名称 | 冀教版数学七年级下·7.1命题(第2课时)教学课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:22:42 | ||
图片预览





文档简介
(共18张PPT)
第七章 相交线与平行线
第七章 相交线与平行线
7.1 命题
第2课时 说理
学 习 目 标
1
2
理解和掌握说理、基本事实、定理及演绎推理的概念.(重点)
能对真命题的成立进行简单的说理。
新课导入
前面我们学过什么叫做命题,命题又分为真命题和假命题.
同时,学习了判断一个命题是假命题的方法——举反例。
那么,我们如何证明一个命题是真命题呢?
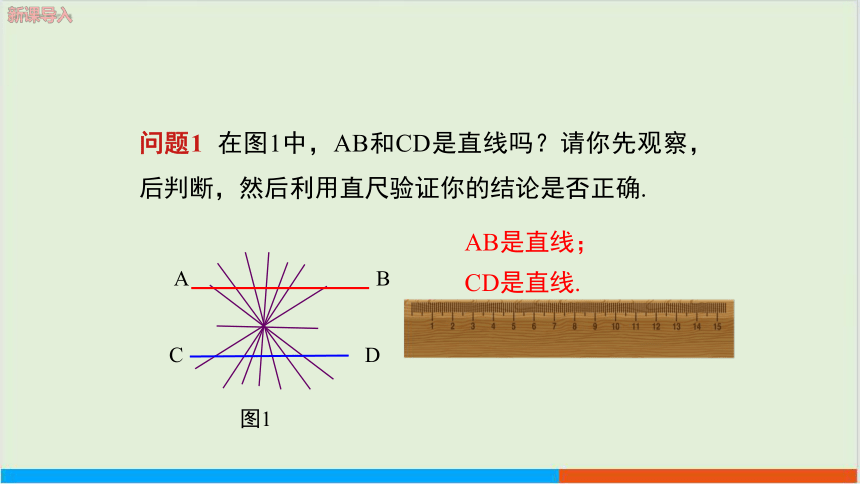
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
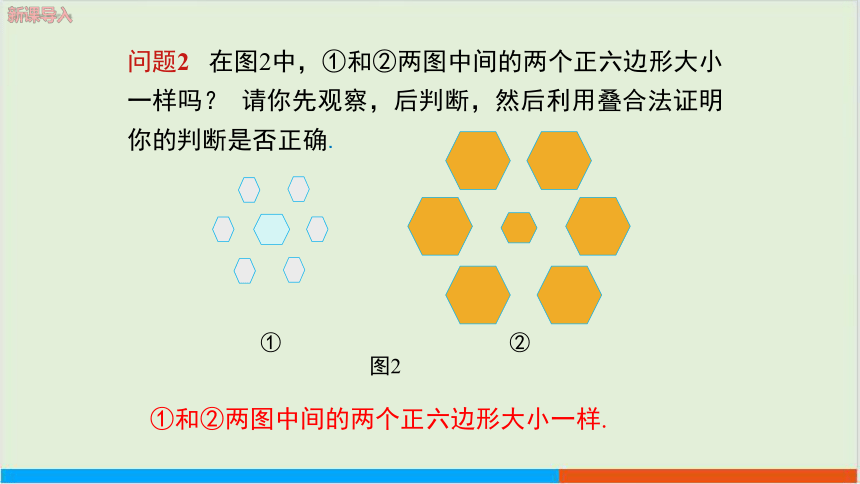
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
则a3=13=1,b3=(-1)3=-1,则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学过的基本事实有哪些呢?
知识讲解
在修建公路时,有时需将弯路改直缩短路程,这是根据什么基本事实?
两点之间的连线中,线段最短.
过平面上的两点,有且只有一条直线.
射击的时候瞄准目标
是依据什么基本事实?
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4整除.
实验、归纳是常用的发现命题的方法.
问题2 通过说理,验证你的猜想正确与否.
说明:设a=2k-1,b=2k+1,其中k是整数.(符合命题的条件)
则a+b=2k-1+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD
(等量加等量,和相等),
所以 AD=CB(线段和的定义).
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
随堂训练
3,在括号内填上推理的依据。
命题:如图,如果∠ABC=∠A'B'C',∠1=∠2,那么∠3=∠4.
理由:因为∠ABC=∠A'B'C',∠1=∠2 ( )
所以∠ABC—∠1=∠A'B'C'—∠2 ( )
又因为∠3=∠ABC—∠1,∠4=∠A'B'C'—∠2 (两角
差的定义)
所以∠3=∠4 (等量代换)
已知
等式的性质
4.如图,已知线段AB,点C,M都是线段AB上的点,若M是BC的中点,则AC+AB=2AM,请在下面说理过程的括号内填写适当的说明依据.
A
C
M
B
理由:因为M是BC的中点(已知),
所以 BC=2MC ( ).
因为 AM=AC+CM ( ),
线段中点的定义
线段和的定义
所以 2AM=2AC+2CM ( ),
等式的性质2
所以 2AM=2AC+BC ( ),
等量代换
又因为 AB=AC+BC ( ),
线段和的定义
所以 2AM=AC+BC ( ),
等量代换
课堂小结
说理 演绎推理
基本事实
定理
定义
第七章 相交线与平行线
第七章 相交线与平行线
7.1 命题
第2课时 说理
学 习 目 标
1
2
理解和掌握说理、基本事实、定理及演绎推理的概念.(重点)
能对真命题的成立进行简单的说理。
新课导入
前面我们学过什么叫做命题,命题又分为真命题和假命题.
同时,学习了判断一个命题是假命题的方法——举反例。
那么,我们如何证明一个命题是真命题呢?
问题1 在图1中,AB和CD是直线吗?请你先观察,后判断,然后利用直尺验证你的结论是否正确.
图1
A
B
C
D
AB是直线;
CD是直线.
问题2 在图2中,①和②两图中间的两个正六边形大小一样吗? 请你先观察,后判断,然后利用叠合法证明你的判断是否正确.
图2
①
②
①和②两图中间的两个正六边形大小一样.
问题3 如果a=-b,那么a2=b2.由此得出:当a=-b时,a3=b3.你认为后一个命题正确吗?为什么?
后一个命题不正确.
说明:设a=1,b=-1,则a=-b.(符合命题的条件)
则a3=13=1,b3=(-1)3=-1,则a3≠b3.(不符合命题的结论)
所以命题“当a=-b时,a3=b3”是个假命题.
由观察、实验、归纳和类比等方法得出的命题,可能是真命题,也可能是假命题.判断命题的真假需要说明理由,这个过程就是说理.
有些命题经过实践经验被公认为真命题,我们把这样的命题叫做基本事实.
我们学过的基本事实有哪些呢?
知识讲解
在修建公路时,有时需将弯路改直缩短路程,这是根据什么基本事实?
两点之间的连线中,线段最短.
过平面上的两点,有且只有一条直线.
射击的时候瞄准目标
是依据什么基本事实?
观察相邻两个奇数的和:
1
3
5
7
9
···
4
8
12
16
···
问题1 相邻两个奇数的和与4之间有什么关系?请提出你的猜想.
相邻两个奇数的和都能被4整除.
实验、归纳是常用的发现命题的方法.
问题2 通过说理,验证你的猜想正确与否.
说明:设a=2k-1,b=2k+1,其中k是整数.(符合命题的条件)
则a+b=2k-1+(2k+1)=4k.(符合命题的结论)
所以“相邻两个奇数的和能被4整除”这个命题是真命题.
例 如图,说明“如果C,D是线段AB上的两点,且AC=BD,那么AD=CB”是真命题.
A
C
D
B
理由:因为 AC=DB(已知),
所以 AC+CD=DB+CD
(等量加等量,和相等),
所以 AD=CB(线段和的定义).
依据已有的事实(包括定义、基本事实、已被确认的真命题),按照确定的规则,得到某个具体的结论的推理就是演绎推理.
有些真命题,它们的正确性已经过演绎推理得到证实,并被作为判定其他命题真假的依据,这些命题叫做定理.
1.下列问题用到推理的是( )
A.根据a=10,b=10,得到a=b
B.观察得到了三角形有三个角
C.老师告诉了我们关于金字塔的许多奥秘
D.由经验可知过两点有且只有一条直线
A
2.下列说法中不正确的是( )
A.证实命题正确与否的推理过程就是说理
B.命题是判断一件事的语句
C.基本事实的正确与否必须通过推理的方法来证实
D.定理都是真命题,但真命题不一定是定理
C
随堂训练
3,在括号内填上推理的依据。
命题:如图,如果∠ABC=∠A'B'C',∠1=∠2,那么∠3=∠4.
理由:因为∠ABC=∠A'B'C',∠1=∠2 ( )
所以∠ABC—∠1=∠A'B'C'—∠2 ( )
又因为∠3=∠ABC—∠1,∠4=∠A'B'C'—∠2 (两角
差的定义)
所以∠3=∠4 (等量代换)
已知
等式的性质
4.如图,已知线段AB,点C,M都是线段AB上的点,若M是BC的中点,则AC+AB=2AM,请在下面说理过程的括号内填写适当的说明依据.
A
C
M
B
理由:因为M是BC的中点(已知),
所以 BC=2MC ( ).
因为 AM=AC+CM ( ),
线段中点的定义
线段和的定义
所以 2AM=2AC+2CM ( ),
等式的性质2
所以 2AM=2AC+BC ( ),
等量代换
又因为 AB=AC+BC ( ),
线段和的定义
所以 2AM=AC+BC ( ),
等量代换
课堂小结
说理 演绎推理
基本事实
定理
定义
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
