16.2二次根式的运算(第1课时二次根式的乘法与积的算术平方根) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 16.2二次根式的运算(第1课时二次根式的乘法与积的算术平方根) 教学课件 沪科版初中数学八年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览








文档简介
(共29张PPT)
16.2 二次根式的运算
第 16章 二次根式
第1课时 二次根式的乘法与积的算术平方根
学 习 目 标
理解二次根式的乘法法则.(重点)
1
2
会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算.(难点)
理解积的算术平方根的性质.
3
复习巩固
1.二次根式的概念:一般地,我们把形如
的式子叫做二次根式.
“
“ ”叫做二次根号,a叫做被开方数.
2.二次根式的性质:
(1)
的性质:
,即二次根式的被开方数非负;
,即二次根式的值非负.
(2)
的性质:
=|a|=
新课导入
问题1 运用运载火箭发射航天行器时,火箭必须达到一定的速度(第一宇宙速度),才能克服地球的引力,从而将飞船送入环地球运行的轨道.第一宇宙速度v与地球半径R之间存在如下关系:v12=gR,其中g是重力加速度.请用含g,R的代数式表示出第一宇宙速度v1.
第一宇宙速度v1可以表示为 .
问题2 飞行器脱离地心引力,进入围绕太阳运行的轨道所需要的速度称为第二宇宙速度.第二宇宙速度为v2= v1,请结合问题1用含g,R的代数式表示出第二宇宙速度v2.
第二宇宙速度v2可以表示为 .
思考 若已知地球半径R≈ 6371 km及重力加速度≈10m/s2,
要求第二宇宙速度,本质是把两个二次根式相乘,该怎么乘呢?
新课导入
(1) ___×___=___;
=_________ ;
计算下列各式:
(2) ___×___=____;
(3) ___×___=____;
=_________ ;
= _________ .
2
3
6
4
5
20
5
6
30
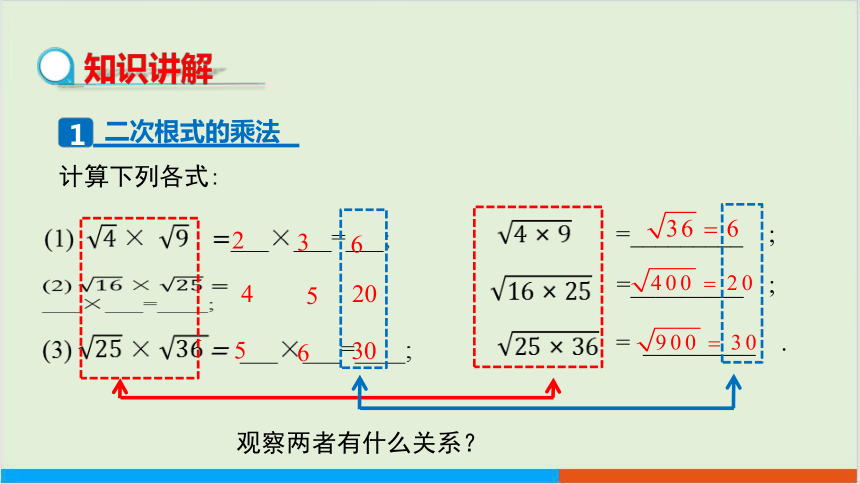
观察两者有什么关系?
二次根式的乘法
知识讲解
1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考:你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
知识讲解
求证:
证明:根据积的乘方法则,有
就是ab算术平方根.
又∵ 表示ab算术平方根,
∴ .
知识讲解
也可以说成:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
归纳总结
知识讲解
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般地,
这个性质常称为“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
积的算术平方根的性质
知识讲解
2
二次根式的乘法法则的推广:
多个二次根式相乘时此法则也适用,即
当二次根号外有因数(式)时,可以类比单项式乘单
项式的法则计算,即根号外的因数(式)的积作为根
号外的因数(式),被开方数的积作为被开方数,即
归纳总结
知识讲解
计算:
归纳:(3)只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即 .
可先用乘法结合律,再运用二次根式的乘法法则
例1
典例讲解
知识讲解
解:
1.计算:
跟踪训练
知识讲解
(1) × ;
(2) × ;
(3) × ;
(4) × .
.
解:
(1) × = ;
(2) × = = ;
(3) × = = =18 ;
(4) × = = .
计算:
解:
归纳:当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即 .
问题 你还记得单项式乘单项式法则吗?
试回顾如何计算3a2·2a3= .
6a5
提示:可类比上面的计算哦
例2
知识讲解
;
2.计算:
跟踪训练
知识讲解
.
(2) .
.
解:
=
=
×
=9
;
(2) = .
(-3)× × 2 ×
=-6
=-6
=-30
.
化简:
例3
解:(1)
=49=36;
(2)
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
知识讲解
(3)
.
知识讲解
(3) =
= ×
×
=
=45.
3. 计算:
提示:
中,a、b必须是非负数.
(1)
知识讲解
解:
(2)
(3)
(2) = ×
=6×16=96;
(3) =
= × =1× =5
跟踪训练
3.如果因式中有平方式(或平方数),应用 =
把这个因式(或因数)开出来,将二次根 式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
知识讲解
归纳:
1.若 ,则 ( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
A
2.下列运算正确的是 ( )
A.
B.
C.
D.
D
随 堂 训 练
3. 计算:
随堂训练
;
3. 计算:
随堂训练
;
随堂训练
4.化简:
(1) ;(2) ;(3) ;(4) .
(a≥0,b≥0)
解:(1) =2 ;
(2) = 3 ;
(3) =2 ;
(4 )
=2ab .
.
5.计算:
;
随堂训练
5.
随堂训练
所以
=610=60.
随堂训练
6.设长方形的面积为S,相邻两边分别为a、b.
,求S.
解:S = ab =
=
=
随堂训练
二次根式乘法
法则
性质
拓展
课堂小结
16.2 二次根式的运算
第 16章 二次根式
第1课时 二次根式的乘法与积的算术平方根
学 习 目 标
理解二次根式的乘法法则.(重点)
1
2
会运用二次根式的乘法法则和积的算术平方根的性质进行简单运算.(难点)
理解积的算术平方根的性质.
3
复习巩固
1.二次根式的概念:一般地,我们把形如
的式子叫做二次根式.
“
“ ”叫做二次根号,a叫做被开方数.
2.二次根式的性质:
(1)
的性质:
,即二次根式的被开方数非负;
,即二次根式的值非负.
(2)
的性质:
=|a|=
新课导入
问题1 运用运载火箭发射航天行器时,火箭必须达到一定的速度(第一宇宙速度),才能克服地球的引力,从而将飞船送入环地球运行的轨道.第一宇宙速度v与地球半径R之间存在如下关系:v12=gR,其中g是重力加速度.请用含g,R的代数式表示出第一宇宙速度v1.
第一宇宙速度v1可以表示为 .
问题2 飞行器脱离地心引力,进入围绕太阳运行的轨道所需要的速度称为第二宇宙速度.第二宇宙速度为v2= v1,请结合问题1用含g,R的代数式表示出第二宇宙速度v2.
第二宇宙速度v2可以表示为 .
思考 若已知地球半径R≈ 6371 km及重力加速度≈10m/s2,
要求第二宇宙速度,本质是把两个二次根式相乘,该怎么乘呢?
新课导入
(1) ___×___=___;
=_________ ;
计算下列各式:
(2) ___×___=____;
(3) ___×___=____;
=_________ ;
= _________ .
2
3
6
4
5
20
5
6
30
观察两者有什么关系?
二次根式的乘法
知识讲解
1
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
思考:你发现了什么规律?你能用字母表示你所发现的规律吗?
猜测:
你能证明这个猜测吗?
知识讲解
求证:
证明:根据积的乘方法则,有
就是ab算术平方根.
又∵ 表示ab算术平方根,
∴ .
知识讲解
也可以说成:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,________不变,________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
在本章中,如果没有特别说明,所有的字母都表示正数.
归纳总结
知识讲解
反过来:
(a≥0,b≥0)
(a≥0,b≥0)
一般地,
这个性质常称为“积的算术平方根的性质”
我们可以运用它来进行二次根式的解题和化简.
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
积的算术平方根的性质
知识讲解
2
二次根式的乘法法则的推广:
多个二次根式相乘时此法则也适用,即
当二次根号外有因数(式)时,可以类比单项式乘单
项式的法则计算,即根号外的因数(式)的积作为根
号外的因数(式),被开方数的积作为被开方数,即
归纳总结
知识讲解
计算:
归纳:(3)只需其中两个结合就可实现转化进行计算,说明二次根式乘法法则同样适合三个及三个以上的二次根式相乘,即 .
可先用乘法结合律,再运用二次根式的乘法法则
例1
典例讲解
知识讲解
解:
1.计算:
跟踪训练
知识讲解
(1) × ;
(2) × ;
(3) × ;
(4) × .
.
解:
(1) × = ;
(2) × = = ;
(3) × = = =18 ;
(4) × = = .
计算:
解:
归纳:当二次根式根号外的因数不为1时,可类比单项式乘单项式的法则计算,即 .
问题 你还记得单项式乘单项式法则吗?
试回顾如何计算3a2·2a3= .
6a5
提示:可类比上面的计算哦
例2
知识讲解
;
2.计算:
跟踪训练
知识讲解
.
(2) .
.
解:
=
=
×
=9
;
(2) = .
(-3)× × 2 ×
=-6
=-6
=-30
.
化简:
例3
解:(1)
=49=36;
(2)
(2)中4a2b3含有像4,a2,b2,这样开的尽方的因数或因式,把它们开方后移到根号外.
知识讲解
(3)
.
知识讲解
(3) =
= ×
×
=
=45.
3. 计算:
提示:
中,a、b必须是非负数.
(1)
知识讲解
解:
(2)
(3)
(2) = ×
=6×16=96;
(3) =
= × =1× =5
跟踪训练
3.如果因式中有平方式(或平方数),应用 =
把这个因式(或因数)开出来,将二次根 式化简 .
1.把被开方数分解因式(或因数) ;
2.把各因式(或因数)积的算术平方根化为每个因
式(或因数)的算术平方根的积;
化简二次根式的步骤:
知识讲解
归纳:
1.若 ,则 ( )
A.x≥6 B.x≥0
C.0≤x≤6 D.x为一切实数
A
2.下列运算正确的是 ( )
A.
B.
C.
D.
D
随 堂 训 练
3. 计算:
随堂训练
;
3. 计算:
随堂训练
;
随堂训练
4.化简:
(1) ;(2) ;(3) ;(4) .
(a≥0,b≥0)
解:(1) =2 ;
(2) = 3 ;
(3) =2 ;
(4 )
=2ab .
.
5.计算:
;
随堂训练
5.
随堂训练
所以
=610=60.
随堂训练
6.设长方形的面积为S,相邻两边分别为a、b.
,求S.
解:S = ab =
=
=
随堂训练
二次根式乘法
法则
性质
拓展
课堂小结
