16.2二次根式的运算(第3课时二次根式的加减) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 16.2二次根式的运算(第3课时二次根式的加减) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
16.2 二次根式的运算
第 16章 二次根式
第3课时 二次根式的加减
学 习 目 标
了解二次根式的加、减运算法则.(重点)
会用二次根式的加、减运算法则进行简单的运算.(难点)
2
3
理解同类二次根式的概念.
1
新 课 导 入
知识回顾
1.同类项的概念:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
2.合并同类项的概念:
把多项式中的同类项合并成一项,叫做合并同类项.
3.合并同类项法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
新 课 导 入
知识回顾
3.最简二次根式:
(1)二次根式被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
4. 化简二次根式的步骤:
(1)把被开方数分解因式(或因数) ;
(2)把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
(3)如果因式中有平方式(或平方数),应用 =|a|把这个因式(或因数)开出来,将二次根式化简.
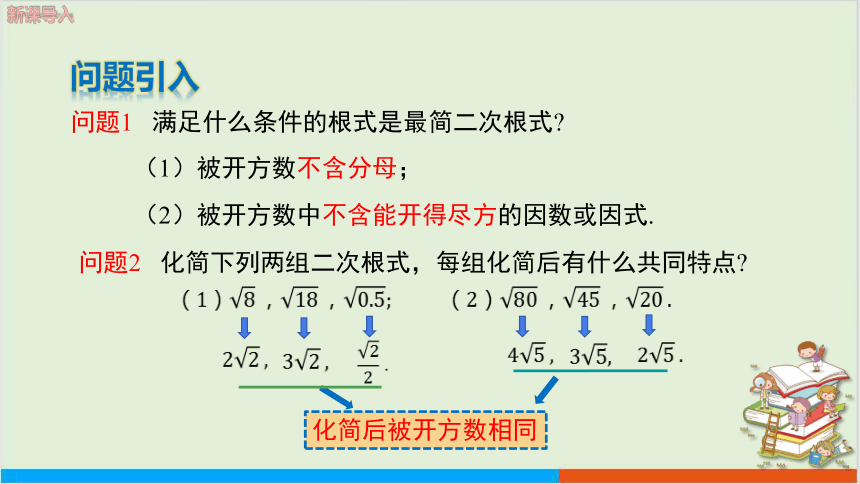
问题1 满足什么条件的根式是最简二次根式
问题2 化简下列两组二次根式,每组化简后有什么共同特点
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
化简后被开方数相同
问题引入
新课导入
探究点一 同类二次根式
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,像这样的二次根式称为同类二次根式.
例如(1)中各式化简后得到
(2)中各式化简后得到
知 识 讲 解
新课导入
探究点二 二次根式的加减
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,像这样的二次根式称为同类二次根式.
例如(1)中各式化简后得到
(2)中各式化简后得到
思考:
(化成最简二次根式)
(结合律)
你发现了什么?
在有理数范围内成立的运算律,在实数范围内仍然成立.
新课导入
+ -
= +4 -5
=(3+4-5)
=2
+ -
阅读教材P10的内容,完成下面的练习.(学生互学)
二次根式的加减
一般地,二次根式加减时,先把各个二次根式化成最简二次根式,再把同类二次根式合并.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
总结
总结
若最简根式 与 可以合并,求的值.
解:由题意,得 解得
所以
归纳:确定可以合并的二次根式中字母取值的方法:
利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
例1
知识讲解
跟踪训练
知识讲解
如果最简二次根式与 可以合并,
那么要使式子 有意义,求x的取值范围.
1.
2.下列二次根式中,与 是同类二次根式的有哪些?
知识讲解
, , , , .
解:与
是同类二次根式的有 , , .
(1)化——将非最简二次根式的二次根式化简;
二次根式的加减的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)合——把被开方数相同的二次根式合并.
知识讲解
计算:
解:
例2
;
知识讲解
跟踪训练
知识讲解
2.计算:(1) ;(2) .
【解】(1) =(3-2)
(2) =7 .
计算:
解:
有括号,先去括号.
例3
(2)
知识讲解
跟踪训练
知识讲解
3.计算:(1) + + ;
(2)3 + - + .
(3)
.
解:(1) + + =3 + +2 = ;
(2)3 + - + =3 +4 -2 + = +5 ;
(3) .
.
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
随 堂 训 练
2.下列计算正确的是( )
A. B.
C. D.
C
3. 与最简二次根式 能合并,则m=_____.
1
4.下列二次根式,不能与 合并的是________(填 序号).
(2)(4)
随堂训练
5.已知一个长方形的长为 ,宽为 ,则其周长为______.
(4)
6.三角形的三边长分别为 则这个三角
形的周长为__________.
7.计算:
(4)
随堂训练
8.计算:
知识讲解
解:
.
(
知识讲解
.
二次根式的加减
法则
注意
运算顺序
运算原理
一般地,二次根式相加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并
运算律同实数的加减一样适用
与实数的运算顺序一样
课 堂 小 结
16.2 二次根式的运算
第 16章 二次根式
第3课时 二次根式的加减
学 习 目 标
了解二次根式的加、减运算法则.(重点)
会用二次根式的加、减运算法则进行简单的运算.(难点)
2
3
理解同类二次根式的概念.
1
新 课 导 入
知识回顾
1.同类项的概念:
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
2.合并同类项的概念:
把多项式中的同类项合并成一项,叫做合并同类项.
3.合并同类项法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
新 课 导 入
知识回顾
3.最简二次根式:
(1)二次根式被开方数不含分母;
(2)被开方数中所有因数(或因式)的幂的指数都小于2.
4. 化简二次根式的步骤:
(1)把被开方数分解因式(或因数) ;
(2)把各因式(或因数)积的算术平方根化为每个因式(或因数)的算术平方根的积;
(3)如果因式中有平方式(或平方数),应用 =|a|把这个因式(或因数)开出来,将二次根式化简.
问题1 满足什么条件的根式是最简二次根式
问题2 化简下列两组二次根式,每组化简后有什么共同特点
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
化简后被开方数相同
问题引入
新课导入
探究点一 同类二次根式
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,像这样的二次根式称为同类二次根式.
例如(1)中各式化简后得到
(2)中各式化简后得到
知 识 讲 解
新课导入
探究点二 二次根式的加减
同类二次根式:
几个二次根式化成最简二次根式后,如果被开方数相同,像这样的二次根式称为同类二次根式.
例如(1)中各式化简后得到
(2)中各式化简后得到
思考:
(化成最简二次根式)
(结合律)
你发现了什么?
在有理数范围内成立的运算律,在实数范围内仍然成立.
新课导入
+ -
= +4 -5
=(3+4-5)
=2
+ -
阅读教材P10的内容,完成下面的练习.(学生互学)
二次根式的加减
一般地,二次根式加减时,先把各个二次根式化成最简二次根式,再把同类二次根式合并.
合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:.
注意:判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
总结
总结
若最简根式 与 可以合并,求的值.
解:由题意,得 解得
所以
归纳:确定可以合并的二次根式中字母取值的方法:
利用被开方数相同,指数都为2,列关于待定字母的方程求解即可.
例1
知识讲解
跟踪训练
知识讲解
如果最简二次根式与 可以合并,
那么要使式子 有意义,求x的取值范围.
1.
2.下列二次根式中,与 是同类二次根式的有哪些?
知识讲解
, , , , .
解:与
是同类二次根式的有 , , .
(1)化——将非最简二次根式的二次根式化简;
二次根式的加减的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)合——把被开方数相同的二次根式合并.
知识讲解
计算:
解:
例2
;
知识讲解
跟踪训练
知识讲解
2.计算:(1) ;(2) .
【解】(1) =(3-2)
(2) =7 .
计算:
解:
有括号,先去括号.
例3
(2)
知识讲解
跟踪训练
知识讲解
3.计算:(1) + + ;
(2)3 + - + .
(3)
.
解:(1) + + =3 + +2 = ;
(2)3 + - + =3 +4 -2 + = +5 ;
(3) .
.
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
随 堂 训 练
2.下列计算正确的是( )
A. B.
C. D.
C
3. 与最简二次根式 能合并,则m=_____.
1
4.下列二次根式,不能与 合并的是________(填 序号).
(2)(4)
随堂训练
5.已知一个长方形的长为 ,宽为 ,则其周长为______.
(4)
6.三角形的三边长分别为 则这个三角
形的周长为__________.
7.计算:
(4)
随堂训练
8.计算:
知识讲解
解:
.
(
知识讲解
.
二次根式的加减
法则
注意
运算顺序
运算原理
一般地,二次根式相加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并
运算律同实数的加减一样适用
与实数的运算顺序一样
课 堂 小 结
