17.1一元二次方程 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 17.1一元二次方程 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览






文档简介
(共25张PPT)
第 17章 一元二次方程
17.1 一元二次方程
理解并灵活运用一元二次方程概念解决有关问题.(重点)
学 习 目 标
1
2
3
理解一元二次方程的概念.(难点)
根据一元二次方程的一般形式,确定各项系数.
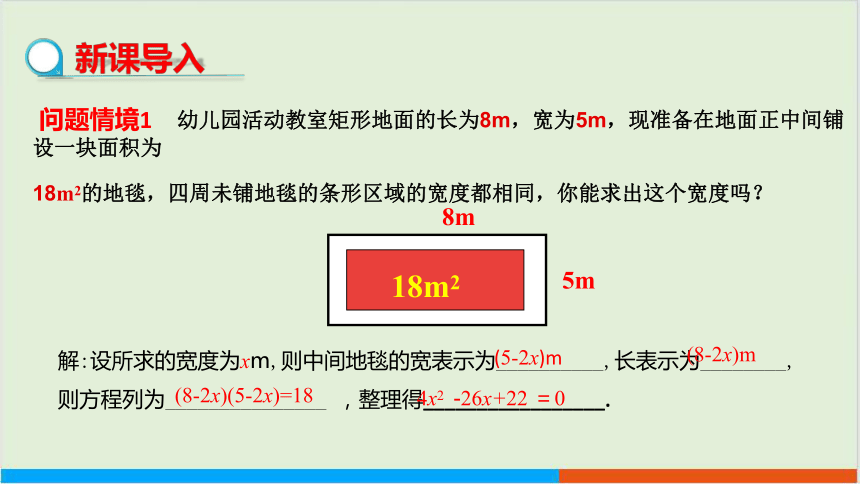
18m2
幼儿园活动教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为
18m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
8m
问题情境1
解:设所求的宽度为xm,则中间地毯的宽表示为__________,长表示为________,
则方程列为_______________ ,整理得_________________.
(5-2x)m
(8-2x)m
(8-2x)(5-2x)=18
新课导入
4x2 -26x+22 =0
5m
桌上有一张矩形纸片,长25cm,宽15cm,在它的四角各剪去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为300cm2,那么纸片各角应剪去的正方形边长为多少厘米?
变式:
15㎝
25㎝
(25-2x)(15-2x )= 300,
300cm2
4x2 -80x+75 =0.
设剪去的正方形边长为x cm,则无盖方盒的底面的长为(25-2x) cm ,
宽为( 15-2x ) cm ,根据题意,可列方程为
整理得
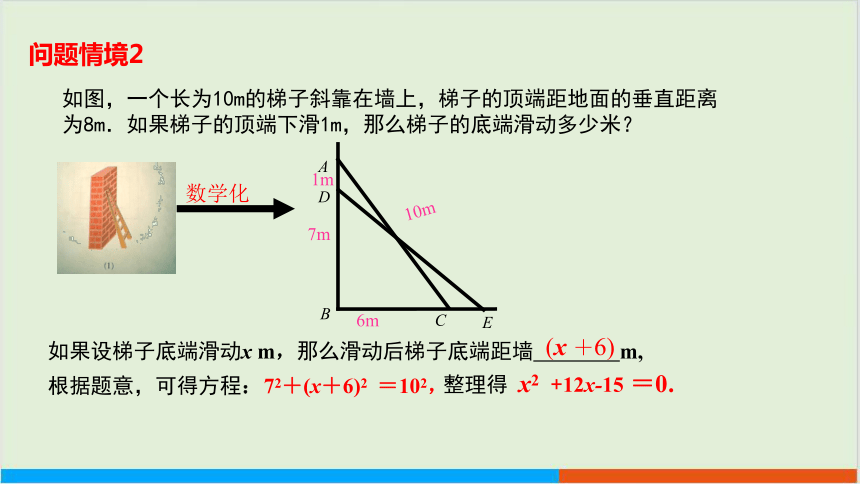
7m
如果设梯子底端滑动x m,那么滑动后梯子底端距墙 m,
根据题意,可得方程:
72+(x+6)2 =102,
(x +6)
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
10m
数学化
问题情境2
A
B
C
1m
D
E
整理得 x2 +12x-15 =0.
6m
要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
分析:
全部比赛共
4×7=28场.
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
即
(x-1)
问题情境3
思考
探究
这四个方程都不是一元一次方程.那么这四个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程(方程两边的分母中不能含有未知数);
②只含一个未知数;
③未知数的最高次数是2.
4x2 -26x+22 =0
4x2 -80x+75 =0
x2 +12x-15 =0
知识讲解
★ 一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的方程,叫做一元二次方程.
(1) 只含一个未知数;
(2) 未知数的最高次数是2;
(3) 整式方程.
满足的条件:
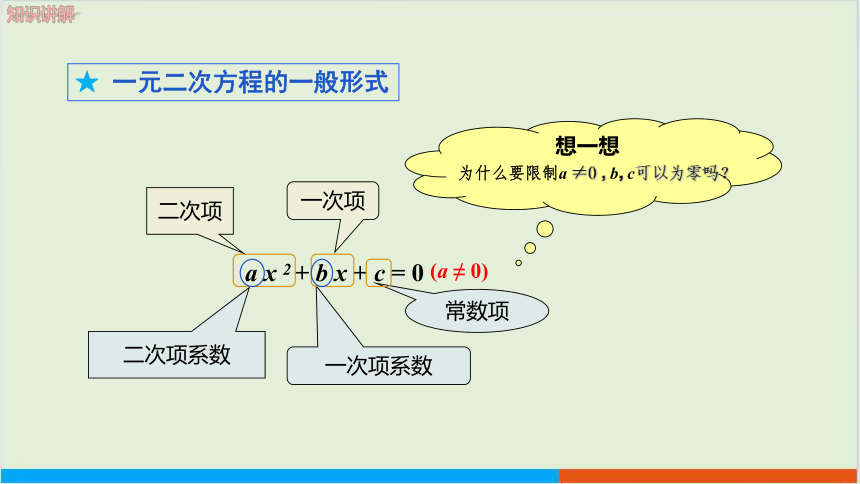
★ 一元二次方程的一般形式
想一想
为什么要限制a ≠0 , b, c可以为零吗?
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
二次项
一次项
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时
ax2+c = 0
当 a ≠ 0 , c = 0时
ax2+bx = 0
当 a ≠ 0 ,b = c =0时
ax2 = 0
总结:若ax2+bx+c=0是一元二次方程只要满足a ≠ 0 ,b , c 可以为任意实数.
为什么一般形式ax2+bx+c=0中要限制a≠0,b、c 可以为零呢?
当b ≠ 0时,为
一元一次方程
一元二次方程
下列方程中哪些是一元二次方程?
是分式
-
y2
2
(8) =0
(7)4 - 7x2=0
(6)x2+2x-3=1+x2
例1
提示:判断一个方程是不是一元二次方程,首先看是不是整式方程;如果是整式方程,再进一步化简整理使方程等号右边为0,最后再观察其是否还具备“只含有一个未知数”“未知数的最高次数是2”这两个条件,若具备,则是一元二次方程,否则不是.
(1)ax2-x=2x2;
(2)(a-1) -2x-7=0.
解:(1)将方程转化为一般形式,得(a-2)x2-x=0,所以当a-2≠0,即a≠2时,原方程是一元二次方程.
(2)由∣a ∣+1 =2,且a-1 ≠0知,当a=-1时,原方程是一元二次方程.
总结:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值.
a为何值时,下列方程为一元二次方程?
例2
解:去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式为
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
注意:(1)一元二次方程的二次项、二次项系数、一次项、一次项系数、常数项等都是针对一般形式而言的;
(2)系数和项均包含它前面的符号.
将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、
一次项和常数项及它们的系数.
例3
★ 一元二次方程的解
使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫做一元二次方程的根.
练一练:
下面哪些数是方程 x2 – 4x +3 = 0 的解
-2 0 ,1,2,3 ,4.
解:1和3.
你注意到了吗?一元二次方程的根可能不止一个.
解:由题意,得
方法总结:已知方程的解求代数式的值,一般先把已知解代入方程,得到等式,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
3(a2+2a)+2 019
=3×2 +2 019
=2 025.
∴ 3a2+6a+2019=
已知a是方程 x2+2x-2=0 的一个实数根, 求 3a2+6a+ 2 019的值.
例4
-1
1
2
★ 知识拓展
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意,得
思考:1.若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
解:由题意,得
∴方程ax2+bx+c=0 (a≠0)的一个根是1.
2. 若 a-b +c=0,4a+2b +c=0 ,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
x=2或x=-1
例5
1.判断下列方程是否为一元二次方程?
(1)3x -x=2 ( )
(2)2(x-1) =3y ( )
(3)3x -2x+5 ( )
( )
(5)(m +5)x +7x-1=0 ( )
√
√
×
×
×
随堂训练
2.方程(2a-4)x2 -2bx+a=0, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程?
解: 若(2a-4)x2 -2bx+a=0是一元二次方程,则二次项系数不为零,
∴2a-4 ≠0,解得a≠2,
即当a≠2时, (2a-4)x2 -2bx+a=0是一元二次方程;
若(2a-4)x2 -2bx+a=0是一元一次方程,则二次项系数为零,一次项系数不为零,
∴2a-4 =0且-2b ≠0,解得a=2,b≠0,
即当a=2,b≠0时, (2a-4)x2 -2bx+a=0是一元一次方程.
3.将下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数、常数项分别是多少:
(1) 2x2=3x-1;
(2)(x+2)(x-2)-2x(x-1)=0.
解:(1) 2x2=3x-1化为一般形式为 2x2-3x+1=0,
∴ 二次项系数、一次项系数、常数项分别是2,-3,1.
(2)(x+2)(x-2)-2x(x-1)=0化为一般形式为 -x2+2x-4=0,
∴ 二次项系数、一次项系数、常数项分别是-1,2,-4.
4.已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值.
解:把x=3代入方程x2+ax+a=0,得
32+3a+a=0,
即9+4a=0,
∴4a=-9,
5.若关于x的一元二次方程(m+2)x2+5x+m2-4=0有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程得m2-4=0,
解得m= ±2.
∵ m+2 ≠0,
∴ m ≠-2,
综上所述,m =2.
6.(只列方程)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
解:设第一个数为x,则另两个数分别为x+1, x+2,依题意得方程:
x (x +1) + x(x +2) + (x +1) (x +2) =242.
x2 +2x-80=0.
整理得
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2
一般形式
对于ax2+bx+c=0 (a ≠0),
其中a≠0 是一元二次方程的必要条件;
确定一元二次方程的二次项系数、一次项系数及常数项要先化为一般式
根
使方程左右两边相等的未知数的值
课堂小结
第 17章 一元二次方程
17.1 一元二次方程
理解并灵活运用一元二次方程概念解决有关问题.(重点)
学 习 目 标
1
2
3
理解一元二次方程的概念.(难点)
根据一元二次方程的一般形式,确定各项系数.
18m2
幼儿园活动教室矩形地面的长为8m,宽为5m,现准备在地面正中间铺设一块面积为
18m2的地毯,四周未铺地毯的条形区域的宽度都相同,你能求出这个宽度吗?
8m
问题情境1
解:设所求的宽度为xm,则中间地毯的宽表示为__________,长表示为________,
则方程列为_______________ ,整理得_________________.
(5-2x)m
(8-2x)m
(8-2x)(5-2x)=18
新课导入
4x2 -26x+22 =0
5m
桌上有一张矩形纸片,长25cm,宽15cm,在它的四角各剪去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的无盖方盒的底面积为300cm2,那么纸片各角应剪去的正方形边长为多少厘米?
变式:
15㎝
25㎝
(25-2x)(15-2x )= 300,
300cm2
4x2 -80x+75 =0.
设剪去的正方形边长为x cm,则无盖方盒的底面的长为(25-2x) cm ,
宽为( 15-2x ) cm ,根据题意,可列方程为
整理得
7m
如果设梯子底端滑动x m,那么滑动后梯子底端距墙 m,
根据题意,可得方程:
72+(x+6)2 =102,
(x +6)
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑动多少米?
10m
数学化
问题情境2
A
B
C
1m
D
E
整理得 x2 +12x-15 =0.
6m
要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
分析:
全部比赛共
4×7=28场.
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
即
(x-1)
问题情境3
思考
探究
这四个方程都不是一元一次方程.那么这四个方程与一元一次方程的区别在哪里?它们有什么共同特点呢?
特点:
①都是整式方程(方程两边的分母中不能含有未知数);
②只含一个未知数;
③未知数的最高次数是2.
4x2 -26x+22 =0
4x2 -80x+75 =0
x2 +12x-15 =0
知识讲解
★ 一元二次方程的概念
只含有一个未知数,并且未知数的最高次数是2的方程,叫做一元二次方程.
(1) 只含一个未知数;
(2) 未知数的最高次数是2;
(3) 整式方程.
满足的条件:
★ 一元二次方程的一般形式
想一想
为什么要限制a ≠0 , b, c可以为零吗?
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
二次项
一次项
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时
ax2+c = 0
当 a ≠ 0 , c = 0时
ax2+bx = 0
当 a ≠ 0 ,b = c =0时
ax2 = 0
总结:若ax2+bx+c=0是一元二次方程只要满足a ≠ 0 ,b , c 可以为任意实数.
为什么一般形式ax2+bx+c=0中要限制a≠0,b、c 可以为零呢?
当b ≠ 0时,为
一元一次方程
一元二次方程
下列方程中哪些是一元二次方程?
是分式
-
y2
2
(8) =0
(7)4 - 7x2=0
(6)x2+2x-3=1+x2
例1
提示:判断一个方程是不是一元二次方程,首先看是不是整式方程;如果是整式方程,再进一步化简整理使方程等号右边为0,最后再观察其是否还具备“只含有一个未知数”“未知数的最高次数是2”这两个条件,若具备,则是一元二次方程,否则不是.
(1)ax2-x=2x2;
(2)(a-1) -2x-7=0.
解:(1)将方程转化为一般形式,得(a-2)x2-x=0,所以当a-2≠0,即a≠2时,原方程是一元二次方程.
(2)由∣a ∣+1 =2,且a-1 ≠0知,当a=-1时,原方程是一元二次方程.
总结:用一元二次方程的定义求字母的值的方法:根据未知数的最高次数等于2,列出关于某个字母的方程,再排除使二次项系数等于0的字母的值.
a为何值时,下列方程为一元二次方程?
例2
解:去括号,得
3x2-3x=5x+10.
移项、合并同类项,得一元二次方程的一般形式为
3x2-8x-10=0.
其中二次项是3x2,系数是3;一次项是-8x,系数是-8;常数项是-10.
注意:(1)一元二次方程的二次项、二次项系数、一次项、一次项系数、常数项等都是针对一般形式而言的;
(2)系数和项均包含它前面的符号.
将方程3x(x-1)=5(x+2)化为一般形式,并分别指出它们的二次项、
一次项和常数项及它们的系数.
例3
★ 一元二次方程的解
使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫做一元二次方程的根.
练一练:
下面哪些数是方程 x2 – 4x +3 = 0 的解
-2 0 ,1,2,3 ,4.
解:1和3.
你注意到了吗?一元二次方程的根可能不止一个.
解:由题意,得
方法总结:已知方程的解求代数式的值,一般先把已知解代入方程,得到等式,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
3(a2+2a)+2 019
=3×2 +2 019
=2 025.
∴ 3a2+6a+2019=
已知a是方程 x2+2x-2=0 的一个实数根, 求 3a2+6a+ 2 019的值.
例4
-1
1
2
★ 知识拓展
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意,得
思考:1.若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
解:由题意,得
∴方程ax2+bx+c=0 (a≠0)的一个根是1.
2. 若 a-b +c=0,4a+2b +c=0 ,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗
x=2或x=-1
例5
1.判断下列方程是否为一元二次方程?
(1)3x -x=2 ( )
(2)2(x-1) =3y ( )
(3)3x -2x+5 ( )
( )
(5)(m +5)x +7x-1=0 ( )
√
√
×
×
×
随堂训练
2.方程(2a-4)x2 -2bx+a=0, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程?
解: 若(2a-4)x2 -2bx+a=0是一元二次方程,则二次项系数不为零,
∴2a-4 ≠0,解得a≠2,
即当a≠2时, (2a-4)x2 -2bx+a=0是一元二次方程;
若(2a-4)x2 -2bx+a=0是一元一次方程,则二次项系数为零,一次项系数不为零,
∴2a-4 =0且-2b ≠0,解得a=2,b≠0,
即当a=2,b≠0时, (2a-4)x2 -2bx+a=0是一元一次方程.
3.将下列一元二次方程化成一般形式,并指出它们的二次项系数、一次项系数、常数项分别是多少:
(1) 2x2=3x-1;
(2)(x+2)(x-2)-2x(x-1)=0.
解:(1) 2x2=3x-1化为一般形式为 2x2-3x+1=0,
∴ 二次项系数、一次项系数、常数项分别是2,-3,1.
(2)(x+2)(x-2)-2x(x-1)=0化为一般形式为 -x2+2x-4=0,
∴ 二次项系数、一次项系数、常数项分别是-1,2,-4.
4.已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值.
解:把x=3代入方程x2+ax+a=0,得
32+3a+a=0,
即9+4a=0,
∴4a=-9,
5.若关于x的一元二次方程(m+2)x2+5x+m2-4=0有一个根为0,求m的值.
二次项系数不为零不容忽视
解:将x=0代入方程得m2-4=0,
解得m= ±2.
∵ m+2 ≠0,
∴ m ≠-2,
综上所述,m =2.
6.(只列方程)三个连续整数两两相乘,再求和,结果为242,这三个数分别是多少?
解:设第一个数为x,则另两个数分别为x+1, x+2,依题意得方程:
x (x +1) + x(x +2) + (x +1) (x +2) =242.
x2 +2x-80=0.
整理得
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2
一般形式
对于ax2+bx+c=0 (a ≠0),
其中a≠0 是一元二次方程的必要条件;
确定一元二次方程的二次项系数、一次项系数及常数项要先化为一般式
根
使方程左右两边相等的未知数的值
课堂小结
