17.2一元二次方程的解法(第2课时配方法) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 17.2一元二次方程的解法(第2课时配方法) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览








文档简介
(共21张PPT)
第 17章 一元二次方程
17.2 一元二次方程的解法
第2课时 配方法
学 习 目 标
1
2
了解配方的概念.
掌握用配方法解一元二次方程及解决有关问题.(重点)
3
探索直接开平方法和配方法之间的区别和联系.(难点)
复 习
新课导入
解下列方程
(1)3x2-1=5;(2)(x-1)2-9=0 ;(3)x2+8x+16=9.
方程(1)(2)可转化成x2=p或(x+n)2= p(p≥0)的形式,由直接开平方法可得方程的根为x= 或x+n= .
方程x2+8x+16=9能不能转化成(x+n)2= p(p≥0)的形式?
想一想
方程(3)怎么解呢?
知识讲解
★ 配方的方法
你还记得吗?填一填下列完全平方公式.
(1) a2+2ab+b2=( )2;
a+b
(2) a2-2ab+b2= ( )2.
a-b
探究交流
做一做:填上适当的数,使下列等式成立
1.x2+12x+ =(x+6)2;
2.x2-6x+ =(x-3)2;
3.x2-4x+ =(x - )2;
4.x2+8x+ =(x + )2.
问题:上面等式的左边的常数项和一次项系数有什么关系?
62
32
22
2
42
4
先对原一元二次方程配方,使它出现完全平方式后,再直接开平方的求解方法,叫做配方法.
对于形如 x2+ax 的式子如何配成完全平方式?
二次项系数为1的完全平方式:常数项等于一次项系数一半的平方.
★ 用配方法解方程
探究交流
怎样解方程x2+6x+4=0?
1.把方程变成(x+n)2=p (p≥0)的形式.
x2+6x+4=0
x2+6x=-4
移项
x2+6x+9=-4+9
两边都加上9
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方.
(x+3)2=5
配方
2.用直接开平方法解方程 (x+3)2=5
(x+3)2=5
开方
x+3=或x+3 =
求解
配方法解方程的基本思路
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为两个一元一次方程求解.
方法归纳
在方程两边都加上一次项系数一半的平方.注意是在二次项系数为1的前提下进行的.
方程配方的方法
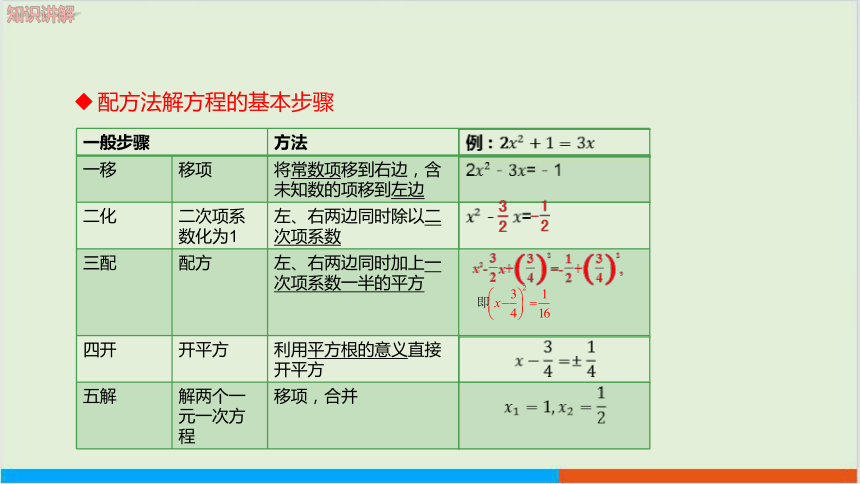
配方法解方程的基本步骤
一般步骤 方法 例:
一移 移项 将常数项移到右边,含未知数的项移到左边 2-=-1
二化 二次项系数化为1 左、右两边同时除以二次项系数 - =
三配 配方 左、右两边同时加上一次项系数一半的平方
四开 开平方 利用平方根的意义直接开平方
五解 解两个一元一次方程 移项,合并
可化为的形式的一元二次方程的根
(1)当>0 时,方程 有两个不相等的实数根:,;
(2)当=0 时,方程 有两个相等的实数根: ;
(3)当<0 时,方程 无实数根.
解下列方程:
例1
∴ x1= x2= -2.
(1)x2+4x+4 = 0 ;
解:移项,得x2+4x = -4.
配方,得x2+4x+22= -4+22,
即(x+2)2=0,
方程的二次项系
数不是1时,为便于
配方,可以将方程
各项的系数除以二
次项系数.
移项和二次项系数化为1这两个步骤能不能交换一下呢
∴ x1 = 1,x2 = .
(2)2 x2x1=0 ;
解:移项,得2 x2 x = 1.
二次项系数化为1,得x2x= .
配方,得x2x+ =,
即 ,
由此可得=,
配方,得
因为实数的平方不会是负数,所以x取任何实数时,(x-1)2都是非负数,即上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
3x2-6x=-4,
x2-2x=- ,
x2-2x+12=- +12,
即
(x-1)2=- .
试用配方法说明:不论k取何实数,多项式k2-4k+5的值必定大于零.
解:k2-4k+5=k2-4k+4+1
=(k-2)2+1
因为(k-2)2≥0,所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
例2
★ 配方法的应用
配方法的应用
类别 解题策略
求最值或证明代数式的值为恒正(或负)
对于一个关于x的二次多项式通过配方转化成a(x+m)2+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值
完全平方式中的配方
如:已知x2-2mx+16是一个完全平方式,所以一次项系数一半的平方等于16,即m2=16,m=±4
利用配方构成非负数和的形式
对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为0,再根据非负数的和为0,各项均为0,从而求解.如:a2+b2-4b+4=0,则a2+(b-2)2=0,即a=0,b=2
1.将二次三项式x2-4x+1配方后得( )
A.(x-2)2+3 B.(x-2)2-3 C.(x+2)2+3 D.(x+2)2-3
2.已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( )
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
3.如果mx2+2(3-2m)x+3m-2=0(m≠0)的左边是一个关于x的完全平方式,则m等于( )
A.1 B.-1 C.1或9 D.-1或9
随堂训练
B
B
C
4.解下列方程:
(1)x2+4x-9=2x-11;(2)x(x+4)=8x+12;
(3)4x2-6x-3=0; (4) 3x2+6x-9=0.
解:x2+2x+2=0,
(x+1)2=-1.
此方程无解.
解:x2-4x-12=0,
(x-2)2=16.
x1=6,x2=-2.
解:x2+2x-3=0,
(x+1)2=4.
x1=-3,x2=1.
解:
5.如图,在Rt△ACB中,∠C=90°,AC=8m,CB=6m,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1m/s,问几秒后△PCQ的面积为Rt△ACB面积的一半?
解:设x秒后△PCQ的面积为Rt△ACB面积的一半.
所以2秒后△PCQ的面积为Rt△ACB面积的一半.
A
C
B
P
Q
根据题意,得
整理,得x2-14x+24=0,
即(x-7)2=25,解得x1=12,x2=2,
x1=12,x2=2都是原方程的根,但x1=12不合题意,舍去.
6.应用配方法求最值.
(1) 2x2 - 4x+5的最小值;
(2) -3x2 + 5x +1的最大值.
解:(1) 2x2 - 4x +5 = 2(x - 1)2 +3 ,
所以当x =1时,有最小值,为3.
(2) -3x2 + 12x - 16 = -3(x - 2)2 - 4 ,
所以当x =2时,有最大值,为-4.
课堂小结
配方法
定义
通过配成完全平方形式解一元二次方程的方法
方法
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方
五解两个一元一次方程
特别提醒:在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
应用
求代数式的最值或证明
在方程两边都配上一次项系数一半的平方
第 17章 一元二次方程
17.2 一元二次方程的解法
第2课时 配方法
学 习 目 标
1
2
了解配方的概念.
掌握用配方法解一元二次方程及解决有关问题.(重点)
3
探索直接开平方法和配方法之间的区别和联系.(难点)
复 习
新课导入
解下列方程
(1)3x2-1=5;(2)(x-1)2-9=0 ;(3)x2+8x+16=9.
方程(1)(2)可转化成x2=p或(x+n)2= p(p≥0)的形式,由直接开平方法可得方程的根为x= 或x+n= .
方程x2+8x+16=9能不能转化成(x+n)2= p(p≥0)的形式?
想一想
方程(3)怎么解呢?
知识讲解
★ 配方的方法
你还记得吗?填一填下列完全平方公式.
(1) a2+2ab+b2=( )2;
a+b
(2) a2-2ab+b2= ( )2.
a-b
探究交流
做一做:填上适当的数,使下列等式成立
1.x2+12x+ =(x+6)2;
2.x2-6x+ =(x-3)2;
3.x2-4x+ =(x - )2;
4.x2+8x+ =(x + )2.
问题:上面等式的左边的常数项和一次项系数有什么关系?
62
32
22
2
42
4
先对原一元二次方程配方,使它出现完全平方式后,再直接开平方的求解方法,叫做配方法.
对于形如 x2+ax 的式子如何配成完全平方式?
二次项系数为1的完全平方式:常数项等于一次项系数一半的平方.
★ 用配方法解方程
探究交流
怎样解方程x2+6x+4=0?
1.把方程变成(x+n)2=p (p≥0)的形式.
x2+6x+4=0
x2+6x=-4
移项
x2+6x+9=-4+9
两边都加上9
二次项系数为1的完全平方式:
常数项等于一次项系数一半的平方.
(x+3)2=5
配方
2.用直接开平方法解方程 (x+3)2=5
(x+3)2=5
开方
x+3=或x+3 =
求解
配方法解方程的基本思路
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为两个一元一次方程求解.
方法归纳
在方程两边都加上一次项系数一半的平方.注意是在二次项系数为1的前提下进行的.
方程配方的方法
配方法解方程的基本步骤
一般步骤 方法 例:
一移 移项 将常数项移到右边,含未知数的项移到左边 2-=-1
二化 二次项系数化为1 左、右两边同时除以二次项系数 - =
三配 配方 左、右两边同时加上一次项系数一半的平方
四开 开平方 利用平方根的意义直接开平方
五解 解两个一元一次方程 移项,合并
可化为的形式的一元二次方程的根
(1)当>0 时,方程 有两个不相等的实数根:,;
(2)当=0 时,方程 有两个相等的实数根: ;
(3)当<0 时,方程 无实数根.
解下列方程:
例1
∴ x1= x2= -2.
(1)x2+4x+4 = 0 ;
解:移项,得x2+4x = -4.
配方,得x2+4x+22= -4+22,
即(x+2)2=0,
方程的二次项系
数不是1时,为便于
配方,可以将方程
各项的系数除以二
次项系数.
移项和二次项系数化为1这两个步骤能不能交换一下呢
∴ x1 = 1,x2 = .
(2)2 x2x1=0 ;
解:移项,得2 x2 x = 1.
二次项系数化为1,得x2x= .
配方,得x2x+ =,
即 ,
由此可得=,
配方,得
因为实数的平方不会是负数,所以x取任何实数时,(x-1)2都是非负数,即上式都不成立,所以原方程无实数根.
解:移项,得
二次项系数化为1,得
3x2-6x=-4,
x2-2x=- ,
x2-2x+12=- +12,
即
(x-1)2=- .
试用配方法说明:不论k取何实数,多项式k2-4k+5的值必定大于零.
解:k2-4k+5=k2-4k+4+1
=(k-2)2+1
因为(k-2)2≥0,所以(k-2)2+1≥1.
所以k2-4k+5的值必定大于零.
例2
★ 配方法的应用
配方法的应用
类别 解题策略
求最值或证明代数式的值为恒正(或负)
对于一个关于x的二次多项式通过配方转化成a(x+m)2+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值
完全平方式中的配方
如:已知x2-2mx+16是一个完全平方式,所以一次项系数一半的平方等于16,即m2=16,m=±4
利用配方构成非负数和的形式
对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为0,再根据非负数的和为0,各项均为0,从而求解.如:a2+b2-4b+4=0,则a2+(b-2)2=0,即a=0,b=2
1.将二次三项式x2-4x+1配方后得( )
A.(x-2)2+3 B.(x-2)2-3 C.(x+2)2+3 D.(x+2)2-3
2.已知x2-8x+15=0,左边化成含有x的完全平方形式,其中正确的是( )
A.x2-8x+(-4)2=31 B.x2-8x+(-4)2=1
C.x2+8x+42=1 D.x2-4x+4=-11
3.如果mx2+2(3-2m)x+3m-2=0(m≠0)的左边是一个关于x的完全平方式,则m等于( )
A.1 B.-1 C.1或9 D.-1或9
随堂训练
B
B
C
4.解下列方程:
(1)x2+4x-9=2x-11;(2)x(x+4)=8x+12;
(3)4x2-6x-3=0; (4) 3x2+6x-9=0.
解:x2+2x+2=0,
(x+1)2=-1.
此方程无解.
解:x2-4x-12=0,
(x-2)2=16.
x1=6,x2=-2.
解:x2+2x-3=0,
(x+1)2=4.
x1=-3,x2=1.
解:
5.如图,在Rt△ACB中,∠C=90°,AC=8m,CB=6m,点P、Q同时由A,B两点出发分别沿AC、BC方向向点C匀速移动,它们的速度都是1m/s,问几秒后△PCQ的面积为Rt△ACB面积的一半?
解:设x秒后△PCQ的面积为Rt△ACB面积的一半.
所以2秒后△PCQ的面积为Rt△ACB面积的一半.
A
C
B
P
Q
根据题意,得
整理,得x2-14x+24=0,
即(x-7)2=25,解得x1=12,x2=2,
x1=12,x2=2都是原方程的根,但x1=12不合题意,舍去.
6.应用配方法求最值.
(1) 2x2 - 4x+5的最小值;
(2) -3x2 + 5x +1的最大值.
解:(1) 2x2 - 4x +5 = 2(x - 1)2 +3 ,
所以当x =1时,有最小值,为3.
(2) -3x2 + 12x - 16 = -3(x - 2)2 - 4 ,
所以当x =2时,有最大值,为-4.
课堂小结
配方法
定义
通过配成完全平方形式解一元二次方程的方法
方法
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方
五解两个一元一次方程
特别提醒:在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
应用
求代数式的最值或证明
在方程两边都配上一次项系数一半的平方
