17.2一元二次方程的解法(第4课时因式分解法) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 17.2一元二次方程的解法(第4课时因式分解法) 教学课件 沪科版初中数学八年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:40 | ||
图片预览








文档简介
(共23张PPT)
第 17章 一元二次方程
17.2 一元二次方程的解法
第4课时 因式分解法
学习目标
1
2
理解用因式分解法解方程的依据.
会用因式分解法解一些特殊的一元二次方程.(重点)
会根据方程的特点选用恰当的方法解一元二次方程.(难点)
3
新课导入
复习交流
(2)因式分解有哪些方法?
2. 说出方程(x+3)(x-5)=0的解。
1. (1)什么是因式分解?
①提公因式法
②公式法
平方差公式
完全平方公式
③十字相乘法
把一个多项式分解成几个整式乘积的形式叫做因式分解.
知识讲解
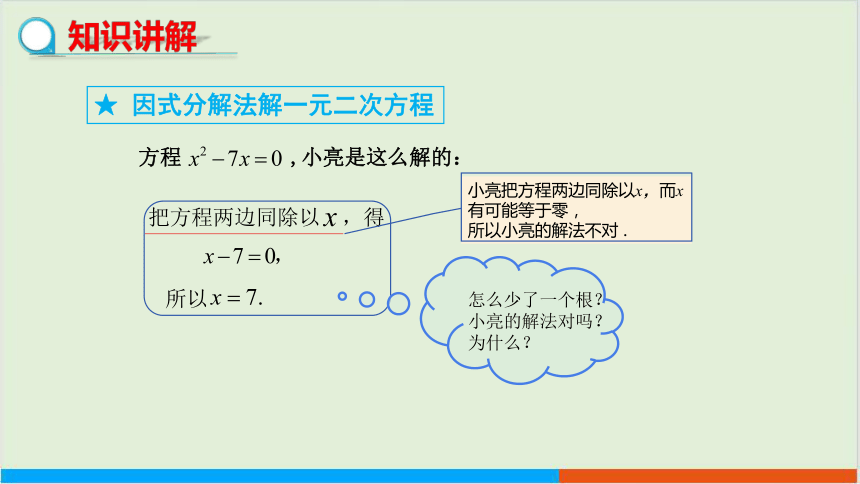
★ 因式分解法解一元二次方程
方程 ,小亮是这么解的:
把方程两边同除以 ,得
所以
小亮把方程两边同除以x,而x有可能等于零,
所以小亮的解法不对 .
怎么少了一个根?
小亮的解法对吗?
为什么?
配方法解方程x2-7x=0.
解:
公式法解方程x2-7x=0.
解:
x27x=0,
∵ a=1,b=7,c=0,
∴ b2-4ac
= (-7)2-4×1×0
=49.
因式分解
如果a · b = 0,
那么 a = 0或 b = 0.
两个因式乘积为 0,说明什么?
或
降次,化为两个一次方程
(解两个一次方程,得出原方程的根)
这种解法是不是很简单?
x2 -7x =0 ①
x(x-7) =0 ②
x =0
x-7=0
通过因式分解,将一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
1.移项:将方程的右边化为0;
2.化积:将方程的左边因式分解为两个一次式的乘积;
3.转化:方程转化为两个一元一次方程;
4.求解:解两个一元一次方程,写出方程两个解.
简记口诀:
右化零 左分解
两因式 各求解
例1
用因式分解法解下列方程
因式分解,得
x2-2x+1 = 0.
( x-1 )( x-1 ) = 0.
所以x1=x2=1.
解:化为一般式为
从而
解:因式分解,得
( 2x + 11 )( 2x- 11 ) = 0.
有 2x + 11 = 0 或 2x - 11= 0,
所以
从而
或
解:把方程的左边进行因式分解,得
,
,
几种常见的用因式分解法求解的方程
(1)形如x2 +bx = 0 的一元二次方程,将左边运用提公因式法因式分解为
x(x+b)= 0,则x = 0 或x+b = 0,即x1= 0, x2 = -b.
(2)形如x2 - a2 = 0 的一元二次方程,将左边用平方差公式因式分解为(x+a)(x-a)= 0,则x+a = 0 或x-a = 0,即x1 = -a, x2 = a.
(3)形如x2 ±2ax+ a2 = 0 的一元二次方程,将左边用完全平方公式因式分解为(x± a )2= 0,则① x+a = 0,即x1 = x2 = -a. ② x-a = 0,即x1 = x2 = a.
(4)形如x2 +(a+b)x+ab = 0 的一元二次方程,将其左边因式分解, 则方程化为(x+a)(x+b)= 0,所以x+a = 0 或x+b = 0,即x1 = -a, x2 = -b.
★ 选择适当的方法解一元二次方程
例2
用适当的方法解下列方程:
(1)2(x-1)2-18 = 0 ;
分析:出现了(x-1)2,并且一次项为0,考虑用直接开平方法.
解:整理,得(x-1)2= 9.
开平方,得x-1 = ±3,
即x-1 = 3 或x-1 = -3,
∴ x1=4,x2=-2.
(2)x2+4x-1 = 0 ;
分析:出现了x2 +4x,接近完全平方式的结构特点,考虑用配方法.
解:原方程变形为x2+4x = 1.
配方,得x2+4x+ 22 = 1+22,即(x+2) 2=5.
可得x+2 = ± ,
∴ x1 = -2+ , x2= -2- .
(3)9(x+1)2=(2x-5)2 ;
分析:移项易发现符合平方差公式,考虑用因式分解法.
解:整理,得[3(x+1)]2-(2x-5)2 = 0.
因式分解,得[3(x+1)+(2x-5)][3(x+1)-(2x-5)]= 0.
可得3(x+1)+(2x-5)= 0 或3(x+1)-(2x-5)= 0,
即5x-2 = 0 或x+8 = 0,
∴ x1 = , x2 = -8.
解:∵ a = 9,b = -12,c = -1,
∴ b 2-4 a c =(-12)2-4×9×(-1)= 144+36 = 180>0,
(4)9x2-12x-1 = 0.
分析:方程的结构没有明显特殊性,考虑公式法.
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
一元二次方程的解法及适用类型
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0), 应选用直接开平方法;
2.若常数项为0( ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
随堂训练
1.下列一元二次方程最适合用因式分解法来解的是( )
A.(x-2)(x+5)=2 B.(x-2)2= x 2-4
C. x 2+5 x -2=0 D.12(2- x)2=3
2.一元二次方程x(x -3)+3- x =0的根是( )
A.1 B.3 C.1和3 D.1和2
C
B
3.已知等腰三角形的腰和底的长分别是一元二次方程x2-4 x +3=0的根,则该三角形的周长可以是( )
A.5 B .7 C.5或7 D.10
B
6.若正数a是一元二次方程x 2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是 .
4.方程x 2=| x |的根是 .
5.如果x 2- x -1=(x +1)0,那么x的值为 .
0,±1
2
5
7.用因式分解法解下列方程:
(1)2(x -3)2=x2-9;
(2)(3x+2)2-4x2=0;
(3)5x(2x-3)=10x-15.
解:2(x-3)2=(x+3)(x-3),
(x-3)[2(x-3)-(x+3)]=0.
解得x1=3,x2=9.
解:(3x+2+2x)(3x+2-2x)=0,
解得x1=-,x2=-2.
解:5x(2x-3)=5(2x-3),
(5x-5)(2x-3)=0,
解得x1=1,x2= .
8.已知三角形的两边长分别为3和7,第三边长是方程x(x-7)-10(x-7)=0的一个根,求这个三角形的周长.
解:解方程x(x-7)-10(x-7)=0,
得x1=7,x2=10.
当x=10时,3+7=10,
∴x2=10不合题意,舍去.
∴这个三角形的周长为3+7+7=17.
课堂小结
因式分解法
概念
步骤
简记口诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0
原理
将方程左边因式分解,右边=0
因式分解的方法有
ma+mb+mc=m(a+b+c);
a2 ±2ab+b2=(a ±b)2;
a2 -b2=(a +b)(a -b)
第 17章 一元二次方程
17.2 一元二次方程的解法
第4课时 因式分解法
学习目标
1
2
理解用因式分解法解方程的依据.
会用因式分解法解一些特殊的一元二次方程.(重点)
会根据方程的特点选用恰当的方法解一元二次方程.(难点)
3
新课导入
复习交流
(2)因式分解有哪些方法?
2. 说出方程(x+3)(x-5)=0的解。
1. (1)什么是因式分解?
①提公因式法
②公式法
平方差公式
完全平方公式
③十字相乘法
把一个多项式分解成几个整式乘积的形式叫做因式分解.
知识讲解
★ 因式分解法解一元二次方程
方程 ,小亮是这么解的:
把方程两边同除以 ,得
所以
小亮把方程两边同除以x,而x有可能等于零,
所以小亮的解法不对 .
怎么少了一个根?
小亮的解法对吗?
为什么?
配方法解方程x2-7x=0.
解:
公式法解方程x2-7x=0.
解:
x27x=0,
∵ a=1,b=7,c=0,
∴ b2-4ac
= (-7)2-4×1×0
=49.
因式分解
如果a · b = 0,
那么 a = 0或 b = 0.
两个因式乘积为 0,说明什么?
或
降次,化为两个一次方程
(解两个一次方程,得出原方程的根)
这种解法是不是很简单?
x2 -7x =0 ①
x(x-7) =0 ②
x =0
x-7=0
通过因式分解,将一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
因式分解法的概念
因式分解法的基本步骤
1.移项:将方程的右边化为0;
2.化积:将方程的左边因式分解为两个一次式的乘积;
3.转化:方程转化为两个一元一次方程;
4.求解:解两个一元一次方程,写出方程两个解.
简记口诀:
右化零 左分解
两因式 各求解
例1
用因式分解法解下列方程
因式分解,得
x2-2x+1 = 0.
( x-1 )( x-1 ) = 0.
所以x1=x2=1.
解:化为一般式为
从而
解:因式分解,得
( 2x + 11 )( 2x- 11 ) = 0.
有 2x + 11 = 0 或 2x - 11= 0,
所以
从而
或
解:把方程的左边进行因式分解,得
,
,
几种常见的用因式分解法求解的方程
(1)形如x2 +bx = 0 的一元二次方程,将左边运用提公因式法因式分解为
x(x+b)= 0,则x = 0 或x+b = 0,即x1= 0, x2 = -b.
(2)形如x2 - a2 = 0 的一元二次方程,将左边用平方差公式因式分解为(x+a)(x-a)= 0,则x+a = 0 或x-a = 0,即x1 = -a, x2 = a.
(3)形如x2 ±2ax+ a2 = 0 的一元二次方程,将左边用完全平方公式因式分解为(x± a )2= 0,则① x+a = 0,即x1 = x2 = -a. ② x-a = 0,即x1 = x2 = a.
(4)形如x2 +(a+b)x+ab = 0 的一元二次方程,将其左边因式分解, 则方程化为(x+a)(x+b)= 0,所以x+a = 0 或x+b = 0,即x1 = -a, x2 = -b.
★ 选择适当的方法解一元二次方程
例2
用适当的方法解下列方程:
(1)2(x-1)2-18 = 0 ;
分析:出现了(x-1)2,并且一次项为0,考虑用直接开平方法.
解:整理,得(x-1)2= 9.
开平方,得x-1 = ±3,
即x-1 = 3 或x-1 = -3,
∴ x1=4,x2=-2.
(2)x2+4x-1 = 0 ;
分析:出现了x2 +4x,接近完全平方式的结构特点,考虑用配方法.
解:原方程变形为x2+4x = 1.
配方,得x2+4x+ 22 = 1+22,即(x+2) 2=5.
可得x+2 = ± ,
∴ x1 = -2+ , x2= -2- .
(3)9(x+1)2=(2x-5)2 ;
分析:移项易发现符合平方差公式,考虑用因式分解法.
解:整理,得[3(x+1)]2-(2x-5)2 = 0.
因式分解,得[3(x+1)+(2x-5)][3(x+1)-(2x-5)]= 0.
可得3(x+1)+(2x-5)= 0 或3(x+1)-(2x-5)= 0,
即5x-2 = 0 或x+8 = 0,
∴ x1 = , x2 = -8.
解:∵ a = 9,b = -12,c = -1,
∴ b 2-4 a c =(-12)2-4×9×(-1)= 144+36 = 180>0,
(4)9x2-12x-1 = 0.
分析:方程的结构没有明显特殊性,考虑公式法.
x2 + px + q = 0 (p2 - 4q ≥0)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) (x + n)=0
一元二次方程的解法及适用类型
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0), 应选用直接开平方法;
2.若常数项为0( ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
随堂训练
1.下列一元二次方程最适合用因式分解法来解的是( )
A.(x-2)(x+5)=2 B.(x-2)2= x 2-4
C. x 2+5 x -2=0 D.12(2- x)2=3
2.一元二次方程x(x -3)+3- x =0的根是( )
A.1 B.3 C.1和3 D.1和2
C
B
3.已知等腰三角形的腰和底的长分别是一元二次方程x2-4 x +3=0的根,则该三角形的周长可以是( )
A.5 B .7 C.5或7 D.10
B
6.若正数a是一元二次方程x 2-5x+m=0的一个根,-a是一元二次方程x2+5x-m=0的一个根,则a的值是 .
4.方程x 2=| x |的根是 .
5.如果x 2- x -1=(x +1)0,那么x的值为 .
0,±1
2
5
7.用因式分解法解下列方程:
(1)2(x -3)2=x2-9;
(2)(3x+2)2-4x2=0;
(3)5x(2x-3)=10x-15.
解:2(x-3)2=(x+3)(x-3),
(x-3)[2(x-3)-(x+3)]=0.
解得x1=3,x2=9.
解:(3x+2+2x)(3x+2-2x)=0,
解得x1=-,x2=-2.
解:5x(2x-3)=5(2x-3),
(5x-5)(2x-3)=0,
解得x1=1,x2= .
8.已知三角形的两边长分别为3和7,第三边长是方程x(x-7)-10(x-7)=0的一个根,求这个三角形的周长.
解:解方程x(x-7)-10(x-7)=0,
得x1=7,x2=10.
当x=10时,3+7=10,
∴x2=10不合题意,舍去.
∴这个三角形的周长为3+7+7=17.
课堂小结
因式分解法
概念
步骤
简记口诀:
右化零 左分解
两因式 各求解
如果a ·b=0,那么a=0或b=0
原理
将方程左边因式分解,右边=0
因式分解的方法有
ma+mb+mc=m(a+b+c);
a2 ±2ab+b2=(a ±b)2;
a2 -b2=(a +b)(a -b)
