冀教版数学七年级下·8.1同底数幂的乘法教学课件
文档属性
| 名称 | 冀教版数学七年级下·8.1同底数幂的乘法教学课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:22:42 | ||
图片预览






文档简介
(共19张PPT)
第八章 整式的乘法
第八章 整式的乘法
8.1 同底数幂的乘法
学 习 目 标
1
2
理解并掌握同底数幂的乘法法则.(重点)
能够运用同底数幂的乘法法则进行相关计算.(难点)
复习:乘方的意义
a
n
指数
幂(乘方的结果)
= a·a· … ·a
n个a
底数
105=10×10×10×10×10
温故知新
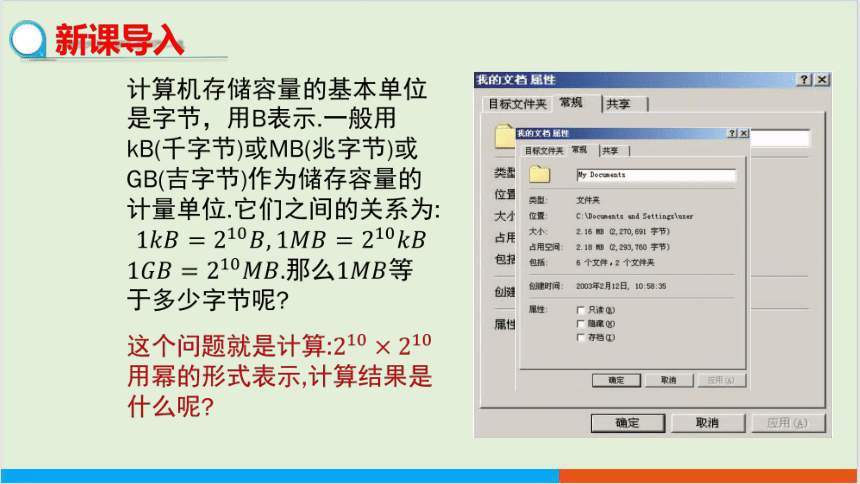
新课导入
回顾乘方的意义:23=2×2×2, 24=2×2×2×2.
1. 用幂表示下列各式的结果:
(1) 24×23=________;
(2) 210×210=________;
(3) ______;
(4) a2·a3= ________;
27
220
a5
知识讲解
2. 通过上面的计算.关于两个同底数幂相乘的结果,你发现了什么规律?你能否把这个规律用公式或者文字语言表示出来呢?
3. 若m,n是正整数,根据你发现的规律,用幂的形式表示am·an .
一般地,对于正整数m,n,有
am·an
=(a·a· … ·a)(a·a· … ·a)= a·a· … ·a= a m+n .
m个a
n个a
(m+n)个a
积的底数与乘数的底数相同,积的指数等于两个乘数的指数的和
· = + (都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
运算形式
运算方法
(同底、乘法)
(底不变、指数相加)
幂的底数必须相同,
相乘时指数才能相加.
例1
把下列各式表示成幂的形式:
(1) 26×23; (2) a2·a4;
(3) xm·xm+1; (4) a·a2·a3.
(1) 26×23=26+3=29 .
(2) a2·a4= a2+4 =a6 .
(3) xm·xm+1 = xm+(m+1)=x2m+1.
(4) a·a2·a3 = a1+2+3 =a6.
解:
(1)同底数幂的乘法法则只有在底数相同时才能使用,
并且底数不变,指数相加,而不是指数相乘.
(2)单个字母或数可以看作指数为1的幂,参与同底数
幂的运算时,不能忽略了幂指数1.
(3)三个或三个以上的同底数幂相乘,幂的运算性质仍然适用。
注 意
练习
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
例2
太阳系的形状像一个以太阳为中心的大圆盘,光通过这个圆盘半径的时间约为2×104 s,光的速度约为3×105 km/s.求太阳系的直径.
2×3×105×2×104
= 12×109(km).
答:太阳系的直径约为12×109 km.
解:
想一想:am+n可以写成哪两个因式的积?
am+n = am · an
填一填:若xm =4 ,xn =5,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
20
4
5
xm
xm
4
4
16
x2m
xn
16
5
80
同底数幂乘法性质的逆用
随堂训练
1.判断下列计算是否正确,并简要说明理由.
(1)3·7=10; (2)a5+a5=a10;(3)y5·y4=y20; (4)p·p2=p2; (5)b4·b4=2b4.
解:
不是同底数幂的乘法
而不是相乘,结果为
;
A
D
D
5.计算:
(1)(-10)5·(-10)2·(-10)3;
(2)
(1)1010;(2)9.
6.计算:
()7
解:m+n
=m·n
=2×3
=6.
解:
课堂小结
am·an=am+n (m,n都是正整数)
同底数幂相乘,底数不变,指数相加.
am·an·ap=am+n+p(m,n,p都是正整数)
同底数幂的乘法性质
第八章 整式的乘法
第八章 整式的乘法
8.1 同底数幂的乘法
学 习 目 标
1
2
理解并掌握同底数幂的乘法法则.(重点)
能够运用同底数幂的乘法法则进行相关计算.(难点)
复习:乘方的意义
a
n
指数
幂(乘方的结果)
= a·a· … ·a
n个a
底数
105=10×10×10×10×10
温故知新
新课导入
回顾乘方的意义:23=2×2×2, 24=2×2×2×2.
1. 用幂表示下列各式的结果:
(1) 24×23=________;
(2) 210×210=________;
(3) ______;
(4) a2·a3= ________;
27
220
a5
知识讲解
2. 通过上面的计算.关于两个同底数幂相乘的结果,你发现了什么规律?你能否把这个规律用公式或者文字语言表示出来呢?
3. 若m,n是正整数,根据你发现的规律,用幂的形式表示am·an .
一般地,对于正整数m,n,有
am·an
=(a·a· … ·a)(a·a· … ·a)= a·a· … ·a= a m+n .
m个a
n个a
(m+n)个a
积的底数与乘数的底数相同,积的指数等于两个乘数的指数的和
· = + (都是正整数)
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
运算形式
运算方法
(同底、乘法)
(底不变、指数相加)
幂的底数必须相同,
相乘时指数才能相加.
例1
把下列各式表示成幂的形式:
(1) 26×23; (2) a2·a4;
(3) xm·xm+1; (4) a·a2·a3.
(1) 26×23=26+3=29 .
(2) a2·a4= a2+4 =a6 .
(3) xm·xm+1 = xm+(m+1)=x2m+1.
(4) a·a2·a3 = a1+2+3 =a6.
解:
(1)同底数幂的乘法法则只有在底数相同时才能使用,
并且底数不变,指数相加,而不是指数相乘.
(2)单个字母或数可以看作指数为1的幂,参与同底数
幂的运算时,不能忽略了幂指数1.
(3)三个或三个以上的同底数幂相乘,幂的运算性质仍然适用。
注 意
练习
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
例2
太阳系的形状像一个以太阳为中心的大圆盘,光通过这个圆盘半径的时间约为2×104 s,光的速度约为3×105 km/s.求太阳系的直径.
2×3×105×2×104
= 12×109(km).
答:太阳系的直径约为12×109 km.
解:
想一想:am+n可以写成哪两个因式的积?
am+n = am · an
填一填:若xm =4 ,xn =5,那么,
(1)xm+n = × = × = ;
(2)x2m = × = × = ;
(3)x2m+n = × = × = .
xm
xn
20
4
5
xm
xm
4
4
16
x2m
xn
16
5
80
同底数幂乘法性质的逆用
随堂训练
1.判断下列计算是否正确,并简要说明理由.
(1)3·7=10; (2)a5+a5=a10;(3)y5·y4=y20; (4)p·p2=p2; (5)b4·b4=2b4.
解:
不是同底数幂的乘法
而不是相乘,结果为
;
A
D
D
5.计算:
(1)(-10)5·(-10)2·(-10)3;
(2)
(1)1010;(2)9.
6.计算:
()7
解:m+n
=m·n
=2×3
=6.
解:
课堂小结
am·an=am+n (m,n都是正整数)
同底数幂相乘,底数不变,指数相加.
am·an·ap=am+n+p(m,n,p都是正整数)
同底数幂的乘法性质
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
