17.5一元二次方程的应用(第3课时传播问题) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 17.5一元二次方程的应用(第3课时传播问题) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览






文档简介
(共17张PPT)
第 17章 一元二次方程
17.5 一元二次方程的应用
第3课时 传播问题
学习目标
1
2
会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
正确分析问题(传播问题)中的数量关系.(难点)
会找出实际问题(传播问题等)中的相等关系并建模解决问题.
3
新课导入
复习交流
(1)列方程解应用题有哪些步骤?
①审题; ②设出未知数;
③列方程;④解方程;
⑤检验方程的解是否符合实际意义;
⑥答.
(2)列方程解应用题应该注意些什么?
①设未知数时必须写清单位;
②列方程时,方程两边各个代数式的单位必须一致;
③解完方程后要检验方程的解是否符合实际意义.
知识讲解
传播问题与一元二次方程
探究
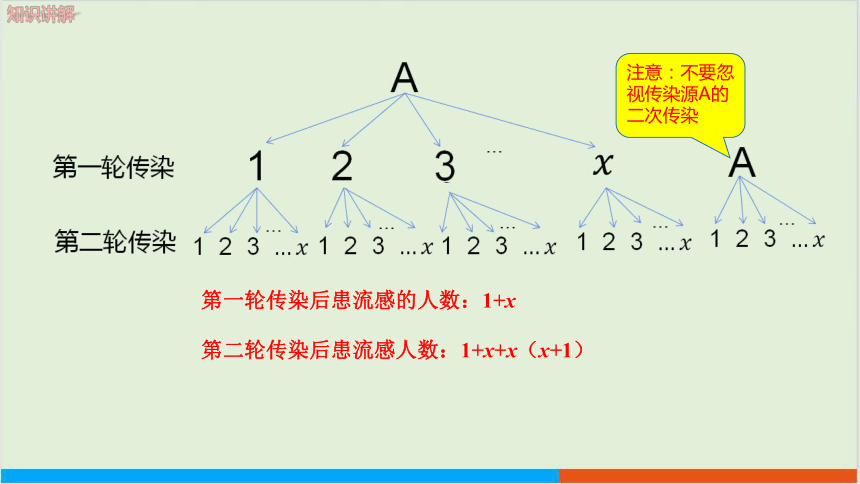
问题: 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 我们把传染源记作A,则其传染示意图如下:
注意:不要忽视传染源A的二次传染
第一轮传染后患流感的人数:1+x
第二轮传染后患流感人数:1+x+x(x+1)
x1=10, x2=-12(不合题意,舍去) .
解方程,得
答:平均一个人传染了10个人.
解:设每轮传染中平均一个人传染了x个人.根据题意,得
即(1+x)2=121,
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
1+x+x(x+1)=121,
思考
如果按照这样的传染速度,三轮传染后有多少人患流感
已知两轮传染后患流感的人数为:121人
第三轮新增的患流感人数为:121×10人
三轮传染后患流感的人数为:121+ 121×10=1331(人)
方法一:
第一轮传染后患流感的人数:1+x=(1+x)1
第二轮传染后患流感人数:1+x+x(x+1)=(1+x)2
第三轮传染后患流感人数:1+x+x(x+1)+x[1+x+x(x+1)]=(1+x)3
答案:三轮传染后的人数是:121(1+x)=121(1+10)=1331(人)或 (1+x)3=(1+10)3=1331(人) .
方法二:
例1 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是111.求每个支干长出多少个小分支?
解:设每个支干长出x个小分支,根据题意,得
1+x+x2=111.
解得x1=10,x2=-11(舍去).
答:每个支干长出10个小分支.
例2 某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
解:设应邀请x支球队参赛,则每队共打(x-1)场比赛,比赛总场数用代数式表示为x(x-1).
根据题意,可列出方程x(x-1)=28.
整理,得x2-x-56=0.
解得x1=8,x2=-7(不合题意,舍去).
答:应邀请8支球队参赛.
例3 有一个两位数,个位数 字与十位数字的和为14,交换位置后,得到新的两位数,比这两个数字的积还大38,求这个两位数.
分析:这是一个数字排列问题,题中有两个等量关系,由前一个等量关系知,个位数字与十位数字均可用同一个未知数表示,这样交换位置后的新两位数也可以用上述未知数表示出来,然后根据后一个等量关系可列方程求解.
解:设个位数字为,则十位数字为14-,
两数字之积为(14-),
两个数字交换位置后的新两位数为10+(14-).
根据题意,得10+(14-)-(14-)=38.
整理,得2-5-24=0,
解得1=8, 2=-3.
因为个位上的数字不可能是负数,
所以2=-3应舍去.
当=8时,14-=6.
所以这个两位数是68.
随堂训练
1.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后会有81台电脑被感染,每轮感染中平均一台电脑会感染几台电脑?设每轮感染中平均一台电脑会感染x台电脑,则x满足的方程是( )
A.1+x2=81 B.(1+x)2=81
C.1+x+x2=81 D.1+x+(1+x)2=81
2.新年里,一个小组有若干人,若每人给小组的其他成员赠送一张贺年卡,则全组送贺卡共72张,此小组人数为( )
A.7 B.8 C.9 D.10
C
B
5.若两个连续整数的积是56,则它们的和是 .
±15
4.一个两位数,个位数字比十位数字少1,且个位数字与十位数字的乘积等于72,则这个两位数是 .
98
3.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
B
解:由题意,得n(n-1)=45.
解得n1=10,n2=-9(舍去).
答:n的值为10.
7.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,问有多少家公司出席了这次交易会?
6.一条直线上有n个点,共形成了45条线段,求n的值.
解:设有x家公司出席了这次交易会,根据题意,得x(x-1)=78.
解得x1=13,x2=-12(舍去).
答:有13家公司出席了这次交易会.
8.一个两位数,个位数字比十位数字大3,且个位数字的平方刚好等于这个两位数,求这个两位数是多少?
解:设这个两位数的个位数字为x,则十位数字为(x-3),由题意,得
x2=10(x-3)+x,解得x1=6,x2=5.
当x=6时,x-3=3;
当x=5时,x-3=2.
答:这个两位数是36或25.
课堂小结
传播问题
数量关系:
第一轮传染后的量=传染前的量× (1+传染速度)
第二轮传染后的量=第一轮传染后的量× (1+传染速度)=传染前的量× (1+传染速度)2
握手问题
送照片问题
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲送乙照片与乙送甲照片是两张照片,故总数不要除以2
传染问题
比赛问题
甲和乙比赛与乙和甲比赛在同一次进行,所以总数要除以2
数字问题
两位数=(十位数字)×10+个位数字
三位数=(百位数字)×100+ (十位数字)×10+个位数字
第 17章 一元二次方程
17.5 一元二次方程的应用
第3课时 传播问题
学习目标
1
2
会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
正确分析问题(传播问题)中的数量关系.(难点)
会找出实际问题(传播问题等)中的相等关系并建模解决问题.
3
新课导入
复习交流
(1)列方程解应用题有哪些步骤?
①审题; ②设出未知数;
③列方程;④解方程;
⑤检验方程的解是否符合实际意义;
⑥答.
(2)列方程解应用题应该注意些什么?
①设未知数时必须写清单位;
②列方程时,方程两边各个代数式的单位必须一致;
③解完方程后要检验方程的解是否符合实际意义.
知识讲解
传播问题与一元二次方程
探究
问题: 有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
分析:设每轮传染中平均一个人传染了x个人. 我们把传染源记作A,则其传染示意图如下:
注意:不要忽视传染源A的二次传染
第一轮传染后患流感的人数:1+x
第二轮传染后患流感人数:1+x+x(x+1)
x1=10, x2=-12(不合题意,舍去) .
解方程,得
答:平均一个人传染了10个人.
解:设每轮传染中平均一个人传染了x个人.根据题意,得
即(1+x)2=121,
注意:列一元二次方程解应用题要注意检验方程的根是否符合题意,要把不符合题意的根舍去.
1+x+x(x+1)=121,
思考
如果按照这样的传染速度,三轮传染后有多少人患流感
已知两轮传染后患流感的人数为:121人
第三轮新增的患流感人数为:121×10人
三轮传染后患流感的人数为:121+ 121×10=1331(人)
方法一:
第一轮传染后患流感的人数:1+x=(1+x)1
第二轮传染后患流感人数:1+x+x(x+1)=(1+x)2
第三轮传染后患流感人数:1+x+x(x+1)+x[1+x+x(x+1)]=(1+x)3
答案:三轮传染后的人数是:121(1+x)=121(1+10)=1331(人)或 (1+x)3=(1+10)3=1331(人) .
方法二:
例1 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数是111.求每个支干长出多少个小分支?
解:设每个支干长出x个小分支,根据题意,得
1+x+x2=111.
解得x1=10,x2=-11(舍去).
答:每个支干长出10个小分支.
例2 某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
解:设应邀请x支球队参赛,则每队共打(x-1)场比赛,比赛总场数用代数式表示为x(x-1).
根据题意,可列出方程x(x-1)=28.
整理,得x2-x-56=0.
解得x1=8,x2=-7(不合题意,舍去).
答:应邀请8支球队参赛.
例3 有一个两位数,个位数 字与十位数字的和为14,交换位置后,得到新的两位数,比这两个数字的积还大38,求这个两位数.
分析:这是一个数字排列问题,题中有两个等量关系,由前一个等量关系知,个位数字与十位数字均可用同一个未知数表示,这样交换位置后的新两位数也可以用上述未知数表示出来,然后根据后一个等量关系可列方程求解.
解:设个位数字为,则十位数字为14-,
两数字之积为(14-),
两个数字交换位置后的新两位数为10+(14-).
根据题意,得10+(14-)-(14-)=38.
整理,得2-5-24=0,
解得1=8, 2=-3.
因为个位上的数字不可能是负数,
所以2=-3应舍去.
当=8时,14-=6.
所以这个两位数是68.
随堂训练
1.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后会有81台电脑被感染,每轮感染中平均一台电脑会感染几台电脑?设每轮感染中平均一台电脑会感染x台电脑,则x满足的方程是( )
A.1+x2=81 B.(1+x)2=81
C.1+x+x2=81 D.1+x+(1+x)2=81
2.新年里,一个小组有若干人,若每人给小组的其他成员赠送一张贺年卡,则全组送贺卡共72张,此小组人数为( )
A.7 B.8 C.9 D.10
C
B
5.若两个连续整数的积是56,则它们的和是 .
±15
4.一个两位数,个位数字比十位数字少1,且个位数字与十位数字的乘积等于72,则这个两位数是 .
98
3.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有飞机场( )
A.4个 B.5个 C.6个 D.7个
B
解:由题意,得n(n-1)=45.
解得n1=10,n2=-9(舍去).
答:n的值为10.
7.在一次商品交易会上,参加交易会的每两家公司之间都要签订一份合同,会议结束后统计共签订了78份合同,问有多少家公司出席了这次交易会?
6.一条直线上有n个点,共形成了45条线段,求n的值.
解:设有x家公司出席了这次交易会,根据题意,得x(x-1)=78.
解得x1=13,x2=-12(舍去).
答:有13家公司出席了这次交易会.
8.一个两位数,个位数字比十位数字大3,且个位数字的平方刚好等于这个两位数,求这个两位数是多少?
解:设这个两位数的个位数字为x,则十位数字为(x-3),由题意,得
x2=10(x-3)+x,解得x1=6,x2=5.
当x=6时,x-3=3;
当x=5时,x-3=2.
答:这个两位数是36或25.
课堂小结
传播问题
数量关系:
第一轮传染后的量=传染前的量× (1+传染速度)
第二轮传染后的量=第一轮传染后的量× (1+传染速度)=传染前的量× (1+传染速度)2
握手问题
送照片问题
甲和乙握手与乙和甲握手在同一次进行,所以总数要除以2
甲送乙照片与乙送甲照片是两张照片,故总数不要除以2
传染问题
比赛问题
甲和乙比赛与乙和甲比赛在同一次进行,所以总数要除以2
数字问题
两位数=(十位数字)×10+个位数字
三位数=(百位数字)×100+ (十位数字)×10+个位数字
