冀教版数学七年级下·8.2幂的乘方与积的乘方(第2课时)教学课件
文档属性
| 名称 | 冀教版数学七年级下·8.2幂的乘方与积的乘方(第2课时)教学课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览



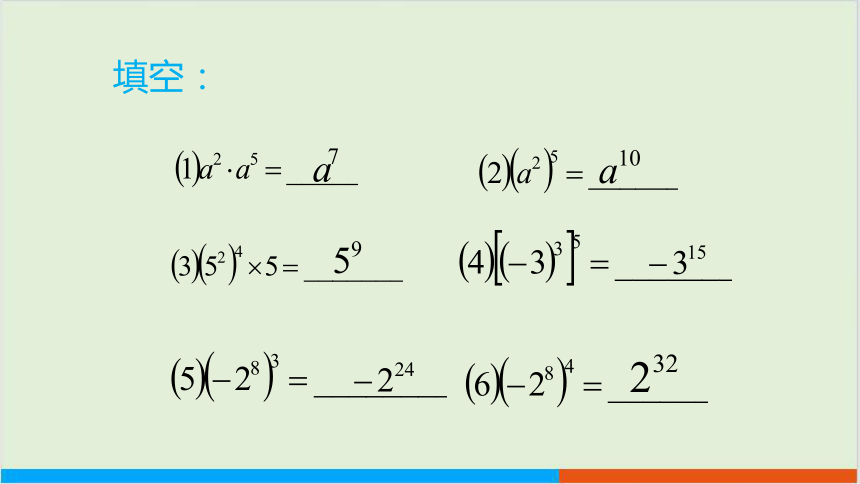



文档简介
(共18张PPT)
第八章 整式的乘法
第八章 整式的乘法
8.2 幂的乘方与积的乘方
第2课时 积的乘方
学 习 目 标
3
1
2
会进行积的乘方运算,会进行有关幂的混合运算.(重点)
经历探索积的乘方运算性质的过程,明确积的乘方是通过乘方的意义和乘法的交换律以及同底数幂的运算性质推导而得来的.(难点)
通过积的乘方性质的探究及应用,体会从特殊到一般的认知规律,从一般到特殊的应用规律.
1.复习提问:叙述并用式子表述下列法则?
(1)同底数幂的乘法:
同底数幂相乘,底数不变,指数相加.
(2)幂的乘方:
幂的乘方,底数不变,指数相乘.
温故知新
填空:
思考 下列两题有什么特点?
(1)
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
知识讲解
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
根据乘方的意义及乘法交换律、结合律进行计算:
(ab)n =
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
思考问题:积的乘方(ab)n =
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
推理验证
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
积的乘方法则
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方运算性质的逆用:
anbn = (ab)n (n为正整数)
例1
计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-3ab2c3)3; (4)(-xmy3m)2.
针对训练
(4)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
(3)(-3ab2c3)3=(-3)3a3b6c9=-27a3b6c9;
例2
随堂训练
1.填空:(1)()2= ;
(2)()3= ;
(3) (2)2= ;
(4)(-)3= ;
(5) = .
2. 计算(a2b)3的结果是( )
A.a2b3 B.a5b3 C.a6b D.a6b3
D
3.下列计算正确的是( )
A.(xy)3=x3y B.(2xy)3=6x3y3
C.(-3x2)3=27x5 D.(a2b)n=a2nbn
4.若(ambn)3=a9b12,则m,n的值等于( )
A.m=9,n=4 B.m=3,n=4
C.m=4,n=3 D.m=9,n=6
D
B
5.下列各式中错误的是( )
A.[(x-y)3]2=(x-y)6
B.(-2a2)4=16a8
C. =- m6n3
D.(-ab3)3=-a3b6
D
6.计算:(1)(a2b)·(a2b)2;
(2) ;
(3)(b-a)·(b-a)3·(a-b)5;
(4) ×1.52 022.
(1); (2)- ;
(3)()9;(4)-1.5.
课堂小结
1、积的乘方运算性质
语言表述:
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
(abc)n = anbncn (n为正整数)
2.积的乘方公式的推广
3.积的乘方运算性质的逆用
anbn = (ab)n (n为正整数)
第八章 整式的乘法
第八章 整式的乘法
8.2 幂的乘方与积的乘方
第2课时 积的乘方
学 习 目 标
3
1
2
会进行积的乘方运算,会进行有关幂的混合运算.(重点)
经历探索积的乘方运算性质的过程,明确积的乘方是通过乘方的意义和乘法的交换律以及同底数幂的运算性质推导而得来的.(难点)
通过积的乘方性质的探究及应用,体会从特殊到一般的认知规律,从一般到特殊的应用规律.
1.复习提问:叙述并用式子表述下列法则?
(1)同底数幂的乘法:
同底数幂相乘,底数不变,指数相加.
(2)幂的乘方:
幂的乘方,底数不变,指数相乘.
温故知新
填空:
思考 下列两题有什么特点?
(1)
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方
我们学过的幂的乘方的运算性质适用吗?
知识讲解
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
根据乘方的意义及乘法交换律、结合律进行计算:
(ab)n =
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
证明:
思考问题:积的乘方(ab)n =
猜想结论:
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
推理验证
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
积的乘方法则
想一想:1.三个或三个以上因式的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
积的乘方公式的推广
2.积的乘方运算性质的逆用:
anbn = (ab)n (n为正整数)
例1
计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-3ab2c3)3; (4)(-xmy3m)2.
针对训练
(4)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
(3)(-3ab2c3)3=(-3)3a3b6c9=-27a3b6c9;
例2
随堂训练
1.填空:(1)()2= ;
(2)()3= ;
(3) (2)2= ;
(4)(-)3= ;
(5) = .
2. 计算(a2b)3的结果是( )
A.a2b3 B.a5b3 C.a6b D.a6b3
D
3.下列计算正确的是( )
A.(xy)3=x3y B.(2xy)3=6x3y3
C.(-3x2)3=27x5 D.(a2b)n=a2nbn
4.若(ambn)3=a9b12,则m,n的值等于( )
A.m=9,n=4 B.m=3,n=4
C.m=4,n=3 D.m=9,n=6
D
B
5.下列各式中错误的是( )
A.[(x-y)3]2=(x-y)6
B.(-2a2)4=16a8
C. =- m6n3
D.(-ab3)3=-a3b6
D
6.计算:(1)(a2b)·(a2b)2;
(2) ;
(3)(b-a)·(b-a)3·(a-b)5;
(4) ×1.52 022.
(1); (2)- ;
(3)()9;(4)-1.5.
课堂小结
1、积的乘方运算性质
语言表述:
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
乘方
相乘
(abc)n = anbncn (n为正整数)
2.积的乘方公式的推广
3.积的乘方运算性质的逆用
anbn = (ab)n (n为正整数)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
