19.2平行四边形(第3课时平行四边形对角线的性质) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.2平行四边形(第3课时平行四边形对角线的性质) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览






文档简介
(共15张PPT)
19.2 平行四边形
第3课时 平行四边形对角线的性质
第19章 四边形
学 习 目 标
掌握平行四边形对角线互相平分的性质.(难点)
让学生能够综合运用平行四边形的性质,并能够利用性质进行简单的推理计算.
1
2
新课导入
发现问题
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的:
老大
老二
老三
老四
如何判断如图的四个小三角形面积相等?
问题1 想一想,平行四边形除了边、角这两个要素
的性质外,对角线有什么性质?
提出猜想
如图,在 ABCD中,连接AC,BD,并设它们相交
于点O.图中共有几对全等三角形?有哪些线段相等?你
发现平行四边形的对角线有什么性质?
D
A
B
C
O
猜想:平行四边形的
对角线互相平分.
A
D
B
C
A
D
B
C
o
我们可以通过下面的动画来
验证.
知识讲解
定理:平行四边形的对角线互相平分.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
定理的证明如下:
例1如图, 平行四边形ABCD的对角线AC、BD相交于点O,AB⊥AC,
AB=3,AD=5.求BD的长度.
A
B
C
D
O
解: ∵ 四边形ABCD是平行四边形
∴ BC=AD=5.
∵AB⊥AC
∴ △ABC是直角三角形.
∴AC=
=
AO=
AC=2.
=
=
,
.
=4.
∴BO=
∴ BD=20B=2 .
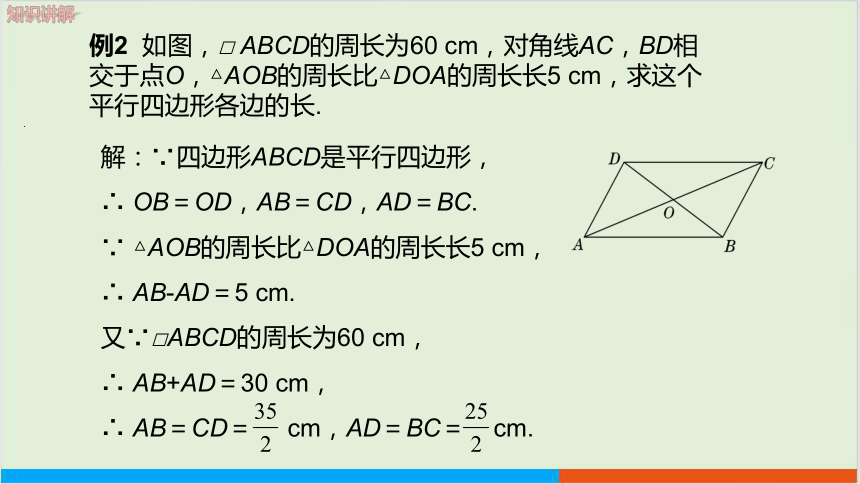
例2 如图,□ ABCD的周长为60 cm,对角线AC,BD相交于点O,△AOB的周长比△DOA的周长长5 cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴ OB=OD,AB=CD,AD=BC.
∵ △AOB的周长比△DOA的周长长5 cm,
∴ AB-AD=5 cm.
又∵□ABCD的周长为60 cm,
∴ AB+AD=30 cm,
∴ AB=CD= cm,AD=BC= cm.
.
例3 如图,在平行四边形ABCD中,AC,BD交于点O,点E,F分别是AO,CO的中点,连接BE,DF,试判断线段BE,DF的关系并证明你的结论.
解:BE=DF,BE∥DF.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OF.
在△OEB和△OFD中,
∴△OEB≌△OFD,
∴BE=DF,∠EBD=∠BDF,
∴BE∥DF.
.
随堂训练
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
D
4
7
3
2. 若平行四边形的一边等于14,则它的两条对角线可能的取值分别是( )
A.8和16 B.6和16 C.2和16 D.20和22
D
3.平行四边形一边长为10,一条对角线长为6,则它的另一条对角线长a的取值范围为( )
A.4C.124.如图, ABC对角线相交于点O,且AC⊥BD,BD=6,BC=5,则 ABCD的面积为 .
4
7
3
B
A
B
C
D
O
24
8
6
10
5.如图,□ABCD的对角线AC,BD相交于点O,EF过点O与AB,CD分别相交于点E,F. 求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO.
在△DFO和△BEO中,
∴△DFO≌△BEO(ASA),
∴OE=OF.
6.如图,平行四边形ABCD的对角线AC,BD相交于点O,AB=5,BC=6.
(1)求OD长的取值范围;
(2)若∠CBD=30°,求OD的长.
C
B
A
D
O
解:(1)∵四边形ABCD是平行四边形,
∴OB=OD=
在△BCD中,∵CD=5,BC=6,
∵1<BD<11,
∴ , .
BD,CD=AB=5,
C
B
A
D
O
(2)过C作CE⊥BD于E,
Rt△CBE中,∵∠CBD=30°,BC=6,
在Rt△CED中,CD2=DE2+CE2,
即52=DE2+32,
解得:DE=4,
E
+4,
∴BD=BE+DE=3
BD=
∴OD=
则OD的长是
∴CE=3,BE=
图形 名称 文字语言 图形语言 符号语言
平行四边形 定义 两组对边分别平行的四边形 ∵AB∥CD,AD∥BC
∴…是平行四边形
性质 平行四边形的对边平行且相等; 对角相等; 对角线互相平分 ∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC AB=CD,AD=BC ∠A=∠C,∠B=∠D
OA=OC,OB=OD
A
B
C
D
A
B
C
D
A
B
C
D
O
课堂小结
19.2 平行四边形
第3课时 平行四边形对角线的性质
第19章 四边形
学 习 目 标
掌握平行四边形对角线互相平分的性质.(难点)
让学生能够综合运用平行四边形的性质,并能够利用性质进行简单的推理计算.
1
2
新课导入
发现问题
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的:
老大
老二
老三
老四
如何判断如图的四个小三角形面积相等?
问题1 想一想,平行四边形除了边、角这两个要素
的性质外,对角线有什么性质?
提出猜想
如图,在 ABCD中,连接AC,BD,并设它们相交
于点O.图中共有几对全等三角形?有哪些线段相等?你
发现平行四边形的对角线有什么性质?
D
A
B
C
O
猜想:平行四边形的
对角线互相平分.
A
D
B
C
A
D
B
C
o
我们可以通过下面的动画来
验证.
知识讲解
定理:平行四边形的对角线互相平分.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
D
A
B
C
O
1
2
3
4
定理的证明如下:
例1如图, 平行四边形ABCD的对角线AC、BD相交于点O,AB⊥AC,
AB=3,AD=5.求BD的长度.
A
B
C
D
O
解: ∵ 四边形ABCD是平行四边形
∴ BC=AD=5.
∵AB⊥AC
∴ △ABC是直角三角形.
∴AC=
=
AO=
AC=2.
=
=
,
.
=4.
∴BO=
∴ BD=20B=2 .
例2 如图,□ ABCD的周长为60 cm,对角线AC,BD相交于点O,△AOB的周长比△DOA的周长长5 cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴ OB=OD,AB=CD,AD=BC.
∵ △AOB的周长比△DOA的周长长5 cm,
∴ AB-AD=5 cm.
又∵□ABCD的周长为60 cm,
∴ AB+AD=30 cm,
∴ AB=CD= cm,AD=BC= cm.
.
例3 如图,在平行四边形ABCD中,AC,BD交于点O,点E,F分别是AO,CO的中点,连接BE,DF,试判断线段BE,DF的关系并证明你的结论.
解:BE=DF,BE∥DF.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OF.
在△OEB和△OFD中,
∴△OEB≌△OFD,
∴BE=DF,∠EBD=∠BDF,
∴BE∥DF.
.
随堂训练
1.在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
D
4
7
3
2. 若平行四边形的一边等于14,则它的两条对角线可能的取值分别是( )
A.8和16 B.6和16 C.2和16 D.20和22
D
3.平行四边形一边长为10,一条对角线长为6,则它的另一条对角线长a的取值范围为( )
A.4
4
7
3
B
A
B
C
D
O
24
8
6
10
5.如图,□ABCD的对角线AC,BD相交于点O,EF过点O与AB,CD分别相交于点E,F. 求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO.
在△DFO和△BEO中,
∴△DFO≌△BEO(ASA),
∴OE=OF.
6.如图,平行四边形ABCD的对角线AC,BD相交于点O,AB=5,BC=6.
(1)求OD长的取值范围;
(2)若∠CBD=30°,求OD的长.
C
B
A
D
O
解:(1)∵四边形ABCD是平行四边形,
∴OB=OD=
在△BCD中,∵CD=5,BC=6,
∵1<BD<11,
∴ , .
BD,CD=AB=5,
C
B
A
D
O
(2)过C作CE⊥BD于E,
Rt△CBE中,∵∠CBD=30°,BC=6,
在Rt△CED中,CD2=DE2+CE2,
即52=DE2+32,
解得:DE=4,
E
+4,
∴BD=BE+DE=3
BD=
∴OD=
则OD的长是
∴CE=3,BE=
图形 名称 文字语言 图形语言 符号语言
平行四边形 定义 两组对边分别平行的四边形 ∵AB∥CD,AD∥BC
∴…是平行四边形
性质 平行四边形的对边平行且相等; 对角相等; 对角线互相平分 ∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC AB=CD,AD=BC ∠A=∠C,∠B=∠D
OA=OC,OB=OD
A
B
C
D
A
B
C
D
A
B
C
D
O
课堂小结
