19.2平行四边形(第4课时利用边的关系判定平行四边形) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.2平行四边形(第4课时利用边的关系判定平行四边形) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览





文档简介
(共25张PPT)
19.2 平行四边形
第4课时 利用边的关系判定平行四边形
第19章 四边形
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
让学生能够应用平行四边形的定义和平行四边形的前两个判定定理判定四边形为平行四边形. (重点、难点)
1
3
2
掌握用两组对边分别相等来判定平行四边形的方法.(重点)
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形还有哪些性质?
知识回顾
答:两组对边分别平行的四边形叫做平行四边形.
答:(1)平行四边形的两组对边分别平行;
(2)平行四边形的对边相等;
(3)平行四边形的对角相等,相邻两角互补;
(4)平行四边形的对角线互相平分.
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
课堂导入
知识讲解
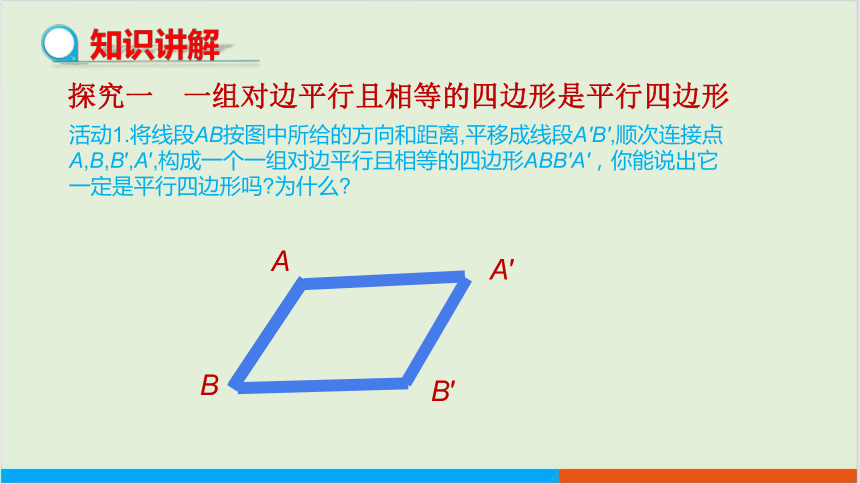
活动1.将线段AB按图中所给的方向和距离,平移成线段A′B′,顺次连接点A,B,B′,A′,构成一个一组对边平行且相等的四边形ABB′A′,你能说出它一定是平行四边形吗 为什么
A
B
A′
B′
探究一 一组对边平行且相等的四边形是平行四边形
B
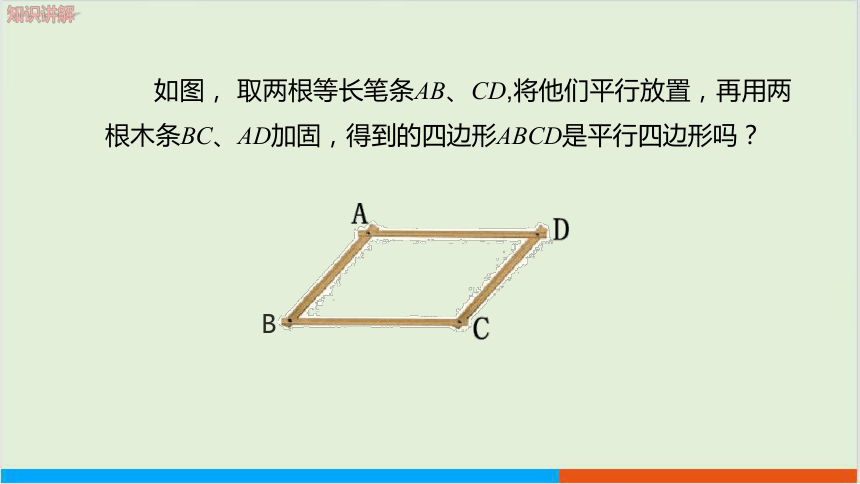
如图, 取两根等长笔条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
1
2
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
证明:连接AC,
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD , AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
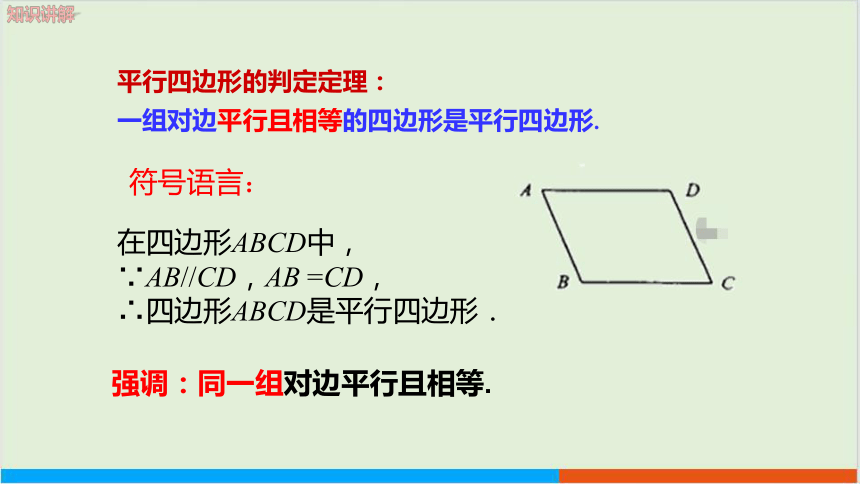
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
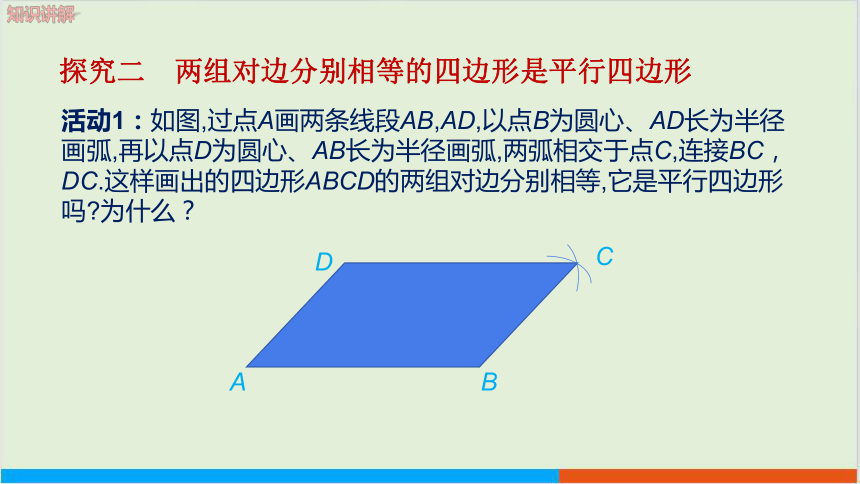
活动1:如图,过点A画两条线段AB,AD,以点B为圆心、AD长为半径画弧,再以点D为圆心、AB长为半径画弧,两弧相交于点C,连接BC,DC.这样画出的四边形ABCD的两组对边分别相等,它是平行四边形吗 为什么?
探究二 两组对边分别相等的四边形是平行四边形
A
B
C
D
活动2:
工具:两对长度分别相等的笔.
动手:能否在平面内用这四根笔摆成一个
平行四边形?
思考:你能说明你所摆出的四边形是
平行四边形吗?
B
已知:如图,在四边形ABCD中,
AB=CD,BC=AD.
求证:四边形ABCD是平行四边形.
证明:方法一 连接AC.
在△ABC和△CDA中
∵ AB=CD , BC=AD ,AC=AC
∴ △ABC≌△CDA,
∴ ∠ACB=∠CAD, ∠DAC=∠BCA
∴ AB∥CD , AD∥CB.
∴ 四边形ABCD是平行四边形(定义).
A
B
C
D
A
B
C
D
方法二
如图,连接AC.
在△ABC和△CDA中,
∵ AB=CD,AD=CB,AC=AC,
∴ △ABC≌△CDA,
∴ ∠ACB=∠CAD,
∴ AB∥CD .
∵AB=CD,
∴ 四边形ABCD是平行四边形(判定定理1).
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
在四边形ABCD中,
∵AB=CD,AD =BC, ∴四边形ABCD是平行四边形.
符号语言:
例1 如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.
分析:首先根据条件证明△AFD≌△CEB, 可得到AD=CB,
∠DAF=∠BCE,可证出AD∥CB,根据一组对边平行且相等的四边形是平行四边形可证出结论.
A
B
C
D
E
F
解:四边形ABCD是平行四边形.证明如下:
∵DF∥BE,∴∠AFD=∠CEB.
又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS),
∴ AD=CB,∠DAF= ∠BCE,
∴ AD∥CB,
∴四边形ABCD是平行四边形.
例2 如图,四边形ABCD中,AB∥CD,∠B=∠D.
求证:四边形ABCD为平行四边形.
证明:连接AC,如图所示:
∵AB∥CD,
∴∠BAC=∠ACD,
在△ABC和△ACD中,
∴△ABC≌△ACD(AAS),∴BC=AD,
∴AB=CD,BC=AD.
∴四边形ABCD为平行四边形.
A
B
C
D
∠B=∠D,
∠BAC=∠ACD,
AC=CA,
随堂训练
1.在下面给出的条件中,能判定四边形ABCD是平行四边形的是( )
A.AB=BC,AD=DC B.AB=AD,AD=BC
C.AB=BC,AD=AB D.AB=CD,AD=BC
2.若AD=8,AB=4,则当BC=____,CD=____时,四边形ABCD是平行四边形.
D
8
4
3. 四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
4.如图,点D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是 ,理由是
.
5.如图,在四边形ABCD中,AD=BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形.
A
B
C
D
l
平行四边形
两组对边分别相等的四边形是平行四边形
AD∥BC或AB=CD
6.如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
7.如图,已知△ABC,分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE.△BCD.△ACF,求证:四边形DEAF是平行四边形.
证明:∵△ABE,△BDC都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°﹣∠DBA,∠ABC=60°﹣∠DBA,
∴∠DBE=∠ABC,
在△DBE和△ABC中,
∴△DBE≌△CBA(SAS),∴DE=AC,
又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FDC,∴DF=AB=AE.
∵DE=AF,EA=DF,
∴四边形DEAF为平行四边形.
BE=AB,
∠DBE=∠CBA,
BD=BC,
A
B
C
D
E
F
8.如图,∠MON=∠PMO,OP=x-3,OM=4,ON=3,MN=5,MP=11-x.求证:四边形OPMN是平行四边形.
O
P
M
N
证明:在△MON中,OM=4,ON=3,MN=5,
∴ OM 2+ON 2=MN 2,∴ △MON是直角三角形.
∴ ∠MON=∠PMO=90°.
在Rt△POM中,OP=x-3,OM=4,MP=11-x,
由勾股定理可得,OM 2+MP 2=OP 2,
即42+(11-x)2=(x-3)2,解得x=8.
∴OP=x-3=8-3=5,MP=11-x=11-8=3,
∴OP=MN,MP=ON,
∴四边形OPMN是平行四边形.
9.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
课堂小结
定义:两组对边分别平行的四边形是平行四边形
判定定理2:两组对边分别相等的四边形是平行四边形
判定定理1:一组对边平行且相等的四边形是平行四边形
边
平行四边形的
判定方法
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法2
A
B
C
D
A
B
C
D
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵AB//CD, AB=CD
∴四边形ABCD是
平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
19.2 平行四边形
第4课时 利用边的关系判定平行四边形
第19章 四边形
学 习 目 标
掌握用一组对边平行且相等来判定平行四边形的方法.(重点)
让学生能够应用平行四边形的定义和平行四边形的前两个判定定理判定四边形为平行四边形. (重点、难点)
1
3
2
掌握用两组对边分别相等来判定平行四边形的方法.(重点)
1.平行四边形的定义是什么?它有什么作用?
2.平行四边形还有哪些性质?
知识回顾
答:两组对边分别平行的四边形叫做平行四边形.
答:(1)平行四边形的两组对边分别平行;
(2)平行四边形的对边相等;
(3)平行四边形的对角相等,相邻两角互补;
(4)平行四边形的对角线互相平分.
为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了,你能说出其中的道理吗?
课堂导入
知识讲解
活动1.将线段AB按图中所给的方向和距离,平移成线段A′B′,顺次连接点A,B,B′,A′,构成一个一组对边平行且相等的四边形ABB′A′,你能说出它一定是平行四边形吗 为什么
A
B
A′
B′
探究一 一组对边平行且相等的四边形是平行四边形
B
如图, 取两根等长笔条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
1
2
从上面的问题中我们可以抽取出如下题目:
已知 AB∥CD,AB=CD,试说明四边形ABCD是平行四边形.
证明:连接AC,
∵AB //CD ,
∴∠1=∠2 .
又 ∵AB =CD , AC =CA ,
∴△ABC≌△CDA .
∴∠BCA=∠DAC .
∴AD //BC .
∴四边形ABCD是平行四边形.
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,
∵AB//CD,AB =CD,
∴四边形ABCD是平行四边形.
符号语言:
强调:同一组对边平行且相等.
活动1:如图,过点A画两条线段AB,AD,以点B为圆心、AD长为半径画弧,再以点D为圆心、AB长为半径画弧,两弧相交于点C,连接BC,DC.这样画出的四边形ABCD的两组对边分别相等,它是平行四边形吗 为什么?
探究二 两组对边分别相等的四边形是平行四边形
A
B
C
D
活动2:
工具:两对长度分别相等的笔.
动手:能否在平面内用这四根笔摆成一个
平行四边形?
思考:你能说明你所摆出的四边形是
平行四边形吗?
B
已知:如图,在四边形ABCD中,
AB=CD,BC=AD.
求证:四边形ABCD是平行四边形.
证明:方法一 连接AC.
在△ABC和△CDA中
∵ AB=CD , BC=AD ,AC=AC
∴ △ABC≌△CDA,
∴ ∠ACB=∠CAD, ∠DAC=∠BCA
∴ AB∥CD , AD∥CB.
∴ 四边形ABCD是平行四边形(定义).
A
B
C
D
A
B
C
D
方法二
如图,连接AC.
在△ABC和△CDA中,
∵ AB=CD,AD=CB,AC=AC,
∴ △ABC≌△CDA,
∴ ∠ACB=∠CAD,
∴ AB∥CD .
∵AB=CD,
∴ 四边形ABCD是平行四边形(判定定理1).
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
在四边形ABCD中,
∵AB=CD,AD =BC, ∴四边形ABCD是平行四边形.
符号语言:
例1 如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE,四边形ABCD是平行四边形吗?请说明理由.
分析:首先根据条件证明△AFD≌△CEB, 可得到AD=CB,
∠DAF=∠BCE,可证出AD∥CB,根据一组对边平行且相等的四边形是平行四边形可证出结论.
A
B
C
D
E
F
解:四边形ABCD是平行四边形.证明如下:
∵DF∥BE,∴∠AFD=∠CEB.
又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS),
∴ AD=CB,∠DAF= ∠BCE,
∴ AD∥CB,
∴四边形ABCD是平行四边形.
例2 如图,四边形ABCD中,AB∥CD,∠B=∠D.
求证:四边形ABCD为平行四边形.
证明:连接AC,如图所示:
∵AB∥CD,
∴∠BAC=∠ACD,
在△ABC和△ACD中,
∴△ABC≌△ACD(AAS),∴BC=AD,
∴AB=CD,BC=AD.
∴四边形ABCD为平行四边形.
A
B
C
D
∠B=∠D,
∠BAC=∠ACD,
AC=CA,
随堂训练
1.在下面给出的条件中,能判定四边形ABCD是平行四边形的是( )
A.AB=BC,AD=DC B.AB=AD,AD=BC
C.AB=BC,AD=AB D.AB=CD,AD=BC
2.若AD=8,AB=4,则当BC=____,CD=____时,四边形ABCD是平行四边形.
D
8
4
3. 四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
提示:本题答案不唯一,如答案也可为AD∥BC.
4.如图,点D是直线l外一点,在l上取两点A,B,连结AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是 ,理由是
.
5.如图,在四边形ABCD中,AD=BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形.
A
B
C
D
l
平行四边形
两组对边分别相等的四边形是平行四边形
AD∥BC或AB=CD
6.如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又 ∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
7.如图,已知△ABC,分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE.△BCD.△ACF,求证:四边形DEAF是平行四边形.
证明:∵△ABE,△BDC都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°﹣∠DBA,∠ABC=60°﹣∠DBA,
∴∠DBE=∠ABC,
在△DBE和△ABC中,
∴△DBE≌△CBA(SAS),∴DE=AC,
又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FDC,∴DF=AB=AE.
∵DE=AF,EA=DF,
∴四边形DEAF为平行四边形.
BE=AB,
∠DBE=∠CBA,
BD=BC,
A
B
C
D
E
F
8.如图,∠MON=∠PMO,OP=x-3,OM=4,ON=3,MN=5,MP=11-x.求证:四边形OPMN是平行四边形.
O
P
M
N
证明:在△MON中,OM=4,ON=3,MN=5,
∴ OM 2+ON 2=MN 2,∴ △MON是直角三角形.
∴ ∠MON=∠PMO=90°.
在Rt△POM中,OP=x-3,OM=4,MP=11-x,
由勾股定理可得,OM 2+MP 2=OP 2,
即42+(11-x)2=(x-3)2,解得x=8.
∴OP=x-3=8-3=5,MP=11-x=11-8=3,
∴OP=MN,MP=ON,
∴四边形OPMN是平行四边形.
9.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵ ∠AEF=∠CFE=90°,
∴ AE∥CF,
∴四边形AFCE是平行四边形.
课堂小结
定义:两组对边分别平行的四边形是平行四边形
判定定理2:两组对边分别相等的四边形是平行四边形
判定定理1:一组对边平行且相等的四边形是平行四边形
边
平行四边形的
判定方法
文字语言 图形语言 几何语言
判定
方法1
定义法
判定方法2
A
B
C
D
A
B
C
D
A
B
C
D
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形
∵AB//CD, AB=CD
∴四边形ABCD是
平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
