19.2平行四边形(第6课时三角形的中位线) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.2平行四边形(第6课时三角形的中位线) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览








文档简介
(共21张PPT)
19.2 平行四边形
第6课时 三角形的中位线
第19章 四边形
学 习 目 标
理解三角形中位线的定义.
理解并掌握三角形中位线的性质定理,能够应用这个定理解决有关的问题.(重点)
通过探索,猜想,证明三角形的中位线定理,进一步发展推理论证的能力.
2
3
1
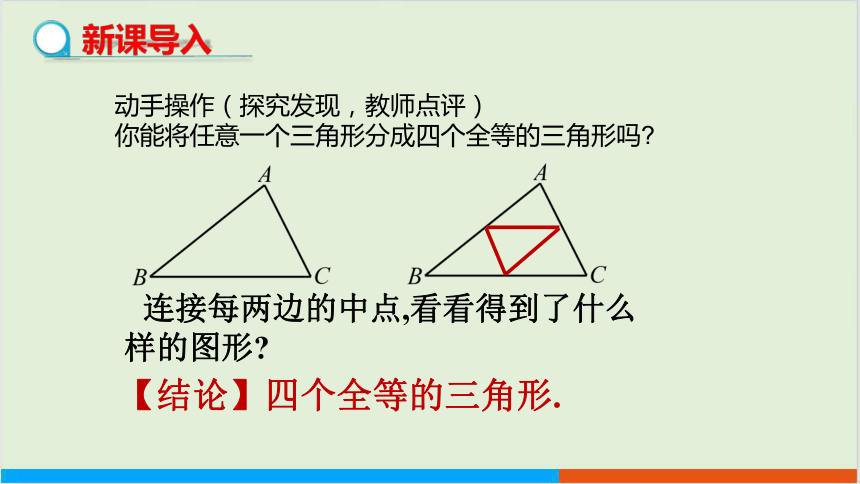
新课导入
动手操作(探究发现,教师点评)
你能将任意一个三角形分成四个全等的三角形吗
连接每两边的中点,看看得到了什么样的图形
【结论】四个全等的三角形.
例1 已知,直线, , , 互相平行,直线AC直线分别交直线 , , 于点A,B,C和点且AB=BC.
求证: .
探究一 一条直线截一组平行线的性质
分析:要证线段AB=BC,可考虑把线段转化在两个全等的三角形中,故过点
作EF∥AC,利用平行四边形的判定和性质证明即可.
A
B
C
E
F
知识讲解
结论:经过三角形一边中点与另一边平行的直线必平分第三边.
证明:过点 作EF∥AC,分别交直线 , 于点E,F.
∴四边形AB E,BCF 都是平行四边形.
∴E =AB, F=BC.
∵AB=BC,
∴E = F.
∵∠ E =∠ F ,∠ F=∠ F,
∴
∴
探究二 三角形的中位线定理
中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
①如果D,E分别为AB,AC的中点,连接DE, 那么DE为△ABC的中位线.
②如果DE为△ABC的中位线,那么 D,E分别为AB,AC的中点.
【问题1】
【问题2】除此之外△ABC还有其它中位线吗 你会画吗 (展示图形)
任意一个三角形都有三条中位线.
【问题3】
请你说出三角形的中线和中位线的区别.
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线.
【问题4】
你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
【问题5】
如图,DE是△ABC的中位线,你能猜出DE与BC有怎样的位置关系和数量关系?能证明你的猜想吗?
猜想:DE∥BC,DE=
BC.
已知:在△ABC中,DE是△ABC的中位线.
求证:DE∥BC ,DE= BC.
证明: (方法一)如图,过点D作DE′∥BC,交AC于点E′,则点E′与点E重合.
∴DE∥BC.
同理,过点D作DF∥AC,交BC于点F,则点F为BC的中点.
∴四边形DFCE是平行四边形.
A
B
C
D
E
F
BC.
∴DE=FC=
(方法二)如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,DE=FE,
∴△ADE≌△CFE(SAS) .
∴AD=CF,∠A=∠ECF.
∴CF∥AB.
∵AD=BD,
∴BD=CF.
∴四边形DBCF是平行四边形.
∴DF∥BC,DF=BC.
BC.
∴DE∥BC,DE=
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
在△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
【例2】如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,则AC的长为( )
A. B.3 C.6 D.9
解析:∵D,E分别为AC,BC的中点,∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,∴∠1=∠3,∴∠1=∠2,∴AD=DF=3,
∴AC=2AD=6.
答案:C.
【例3】如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.
解:∵AM平分∠BAC,CM⊥AM,
∴AD=AC=3,DM=CM.
∵BN=CN,
∴MN为△BCD的中位线,
∴MN= (5-3)=1.
随堂训练
1.如图所示,在△ABC中,点E,F分别为AB,AC的中点.若EF的长为2, 则BC的长为( )
A.1 B.2 C.4 D.8
2.如图所示,在△ABC中,已知AB=8,∠C=90°,∠A=30°,
DE是△ABC的中位线,则DE的长为( )
A.4 B.3 C.2
D.2
C
D
3.如图,C,D分别为EA,EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
A.80° B.90° C.100° D.110°
A
4.如图所示,在□ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=
3 cm,则AB的长为( )
A.3 cm B.6 cm C.9 cm D.12 cm
5.如图所示,在△ABC中,D,E分别是AB,AC的中点,AC=12,
F是DE上一点,连接AF,CF,DF
=1.若∠AFC=
90°,则BC的长度为( )
A.12 B.13 C.14 D.15
B
C
6.直角三角形两条边长分别是6和8,则连接两条直角边中点的线段长是( )
A.3 B.5 C.4或5 D.5或3
7.如图所示,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.求证:EF∥BC.
C
证明:∵CF平分∠ACB,DC=AC,
∴CF是△ACD的中线,∴点F是AD的中点.∵点E是AB的中点,∴EF∥BD,即EF∥BC.
A
B
D
C
F
E
8.已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.求证:四边形EFGH是平行四边形.
证明:如图,连接AC.
∵E,F,G,H分别为各边的中点,
∴EF∥AC,EF= AC.
HG∥AC,HG= AC.
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
9. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
N
M
解:分别找出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
根据是三角形中位线定理.
10.如图,E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OA=OC.
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC, CD=AB,∴AB=CE.
在△ABF和△ECF中,
∴△ABF≌△ECF(ASA),∴BF=CF.
∵OA=OC,∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
课堂小结
1、三角形中位线的定义:
______________________叫做三角形的中位线 .
2、三角形的中位线与中线的区别:中位线是__________的连线;中线是_________的连线.
3、三角形的中位线定理:三角形两边中点的连线线____于三角形的第三边,并且等于第三边的____.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
19.2 平行四边形
第6课时 三角形的中位线
第19章 四边形
学 习 目 标
理解三角形中位线的定义.
理解并掌握三角形中位线的性质定理,能够应用这个定理解决有关的问题.(重点)
通过探索,猜想,证明三角形的中位线定理,进一步发展推理论证的能力.
2
3
1
新课导入
动手操作(探究发现,教师点评)
你能将任意一个三角形分成四个全等的三角形吗
连接每两边的中点,看看得到了什么样的图形
【结论】四个全等的三角形.
例1 已知,直线, , , 互相平行,直线AC直线分别交直线 , , 于点A,B,C和点且AB=BC.
求证: .
探究一 一条直线截一组平行线的性质
分析:要证线段AB=BC,可考虑把线段转化在两个全等的三角形中,故过点
作EF∥AC,利用平行四边形的判定和性质证明即可.
A
B
C
E
F
知识讲解
结论:经过三角形一边中点与另一边平行的直线必平分第三边.
证明:过点 作EF∥AC,分别交直线 , 于点E,F.
∴四边形AB E,BCF 都是平行四边形.
∴E =AB, F=BC.
∵AB=BC,
∴E = F.
∵∠ E =∠ F ,∠ F=∠ F,
∴
∴
探究二 三角形的中位线定理
中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
①如果D,E分别为AB,AC的中点,连接DE, 那么DE为△ABC的中位线.
②如果DE为△ABC的中位线,那么 D,E分别为AB,AC的中点.
【问题1】
【问题2】除此之外△ABC还有其它中位线吗 你会画吗 (展示图形)
任意一个三角形都有三条中位线.
【问题3】
请你说出三角形的中线和中位线的区别.
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线.
【问题4】
你能通过剪拼的方式,将一个三角形拼成一个与其面积相等的平行四边形吗?
【问题5】
如图,DE是△ABC的中位线,你能猜出DE与BC有怎样的位置关系和数量关系?能证明你的猜想吗?
猜想:DE∥BC,DE=
BC.
已知:在△ABC中,DE是△ABC的中位线.
求证:DE∥BC ,DE= BC.
证明: (方法一)如图,过点D作DE′∥BC,交AC于点E′,则点E′与点E重合.
∴DE∥BC.
同理,过点D作DF∥AC,交BC于点F,则点F为BC的中点.
∴四边形DFCE是平行四边形.
A
B
C
D
E
F
BC.
∴DE=FC=
(方法二)如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE, ∠AED=∠CEF,DE=FE,
∴△ADE≌△CFE(SAS) .
∴AD=CF,∠A=∠ECF.
∴CF∥AB.
∵AD=BD,
∴BD=CF.
∴四边形DBCF是平行四边形.
∴DF∥BC,DF=BC.
BC.
∴DE∥BC,DE=
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
在△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
【例2】如图,在△ABC中,D,E分别为AC,BC的中点,AF平分∠CAB,交DE于点F.若DF=3,则AC的长为( )
A. B.3 C.6 D.9
解析:∵D,E分别为AC,BC的中点,∴DE∥AB,∴∠2=∠3.
又∵AF平分∠CAB,∴∠1=∠3,∴∠1=∠2,∴AD=DF=3,
∴AC=2AD=6.
答案:C.
【例3】如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.
解:∵AM平分∠BAC,CM⊥AM,
∴AD=AC=3,DM=CM.
∵BN=CN,
∴MN为△BCD的中位线,
∴MN= (5-3)=1.
随堂训练
1.如图所示,在△ABC中,点E,F分别为AB,AC的中点.若EF的长为2, 则BC的长为( )
A.1 B.2 C.4 D.8
2.如图所示,在△ABC中,已知AB=8,∠C=90°,∠A=30°,
DE是△ABC的中位线,则DE的长为( )
A.4 B.3 C.2
D.2
C
D
3.如图,C,D分别为EA,EB的中点,∠E=30°,∠1=110°,则∠2的度数为( )
A.80° B.90° C.100° D.110°
A
4.如图所示,在□ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=
3 cm,则AB的长为( )
A.3 cm B.6 cm C.9 cm D.12 cm
5.如图所示,在△ABC中,D,E分别是AB,AC的中点,AC=12,
F是DE上一点,连接AF,CF,DF
=1.若∠AFC=
90°,则BC的长度为( )
A.12 B.13 C.14 D.15
B
C
6.直角三角形两条边长分别是6和8,则连接两条直角边中点的线段长是( )
A.3 B.5 C.4或5 D.5或3
7.如图所示,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.求证:EF∥BC.
C
证明:∵CF平分∠ACB,DC=AC,
∴CF是△ACD的中线,∴点F是AD的中点.∵点E是AB的中点,∴EF∥BD,即EF∥BC.
A
B
D
C
F
E
8.已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.求证:四边形EFGH是平行四边形.
证明:如图,连接AC.
∵E,F,G,H分别为各边的中点,
∴EF∥AC,EF= AC.
HG∥AC,HG= AC.
∴ EF∥HG, EF=HG.
∴四边形EFGH是平行四边形.
9. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
N
M
解:分别找出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
根据是三角形中位线定理.
10.如图,E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.
解:AB∥OF,AB=2OF.
证明如下:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OA=OC.
∴∠BAF=∠CEF,∠ABF=∠ECF.
∵CE=DC, CD=AB,∴AB=CE.
在△ABF和△ECF中,
∴△ABF≌△ECF(ASA),∴BF=CF.
∵OA=OC,∴OF是△ABC的中位线,
∴AB∥OF,AB=2OF.
课堂小结
1、三角形中位线的定义:
______________________叫做三角形的中位线 .
2、三角形的中位线与中线的区别:中位线是__________的连线;中线是_________的连线.
3、三角形的中位线定理:三角形两边中点的连线线____于三角形的第三边,并且等于第三边的____.
连接三角形两边中点的线段
中点与中点
顶点与中点
平行
一半
