冀教版数学七年级下·8.5乘法公式(第1课时)教学课件
文档属性
| 名称 | 冀教版数学七年级下·8.5乘法公式(第1课时)教学课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第八章 整式的乘法
第八章 整式的乘法
8.5 乘法公式
第1课时 平方差公式
学 习 目 标
1
2
经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.(重点)
灵活应用平方差公式进行计算和解决实际问题.(难点)
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
温故知新
①(x + 1)( x-1);
②(a+ 2)( a-2);
③(2x+ 1)(2x-1);
④(a + b)(a-b);
问题:计算下列多项式的积,你能发现什么规律?
x2 - 12
a2-22
(2x)2 - 12
a2 - b2
2.上面四个式子中,等号左边两个乘式这间有什么特点?
两个单项式的和与这两个单项式差的乘积
3.乘积合并同类项后是几项式?这个多项式有什么特点?
结果是两项式,且是两个单项式的平方的差
知识讲解
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
平方差公式
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
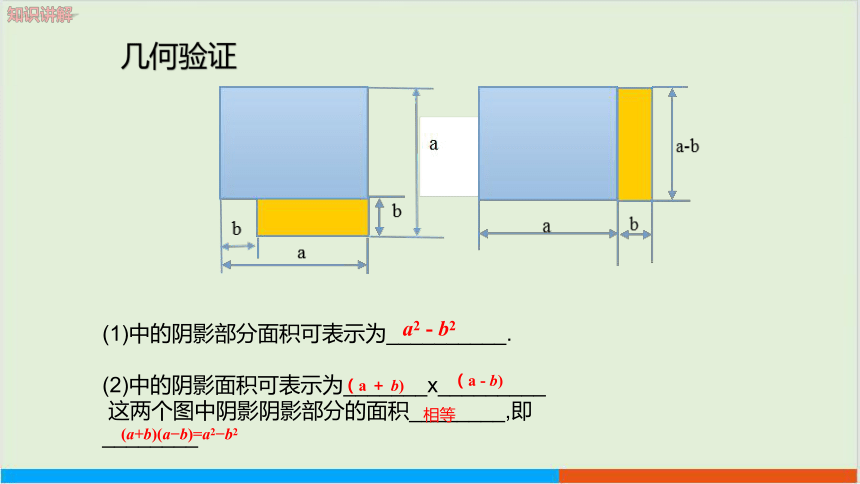
几何验证
(1)中的阴影部分面积可表示为__________.
(2)中的阴影面积可表示为_______x_________
这两个图中阴影阴影部分的面积________,即
________
a2 - b2
(a + b)
(a - b)
相等
(a+b)(a b)=a2 b2
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
例1 计算:
(1)(2x+y)(2x-y);
(2)(x+5y)(x-5y);
(3)(-5a+3b)(-5a-3b).
例2:计算:
(1) 51×49; (2)(3x+4)(3x-4)-(2x+3)(3x-2) .
解: (1) 原式=(50+1)(50-1)
= 502-12
=2500 – 1
=2499;
(2) 原式=(3x)2-42-(6x2+5x-6)
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
随堂训练
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.(2x-5)(2x+5)
C.(-a+b)(a-b) D.(x2-y)(x+y2)
2.下列运算正确的是( )
A.x7÷x5=x2 B.(xy2)2=xy4
C.x2·x5=x10 D.( + )( - )=b-a
B
A
3.填空:
(1
(2
(3
(4)化简的结果是 .
1-9a2
4y2-9x2
3a
3a
x2-1
4.计算:
(1)2;(2)2 491;(3)1.
5.如图2①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图2②所示的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
6.如图所示,小明家有一块“L”形的自留地,现在要分成两块形状、面积相同的部分,种上两种不同的蔬菜,请你来帮小明设计,并算出这块自留地的面积.
7.(选做题)(吉林中考)某同学化简出现了错误,解答过程如下:
原式=第一步)
=(第二步)
=(第三步)
(1)该同学解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
解:(1)二 去括号时有一项没有变号
(2)原式 =
课堂小结
平方差公式
(a+b)(a- b)=
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
第八章 整式的乘法
第八章 整式的乘法
8.5 乘法公式
第1课时 平方差公式
学 习 目 标
1
2
经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.(重点)
灵活应用平方差公式进行计算和解决实际问题.(难点)
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
温故知新
①(x + 1)( x-1);
②(a+ 2)( a-2);
③(2x+ 1)(2x-1);
④(a + b)(a-b);
问题:计算下列多项式的积,你能发现什么规律?
x2 - 12
a2-22
(2x)2 - 12
a2 - b2
2.上面四个式子中,等号左边两个乘式这间有什么特点?
两个单项式的和与这两个单项式差的乘积
3.乘积合并同类项后是几项式?这个多项式有什么特点?
结果是两项式,且是两个单项式的平方的差
知识讲解
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
平方差公式
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
几何验证
(1)中的阴影部分面积可表示为__________.
(2)中的阴影面积可表示为_______x_________
这两个图中阴影阴影部分的面积________,即
________
a2 - b2
(a + b)
(a - b)
相等
(a+b)(a b)=a2 b2
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
例1 计算:
(1)(2x+y)(2x-y);
(2)(x+5y)(x-5y);
(3)(-5a+3b)(-5a-3b).
例2:计算:
(1) 51×49; (2)(3x+4)(3x-4)-(2x+3)(3x-2) .
解: (1) 原式=(50+1)(50-1)
= 502-12
=2500 – 1
=2499;
(2) 原式=(3x)2-42-(6x2+5x-6)
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
随堂训练
1.下列多项式乘法中,可以用平方差公式计算的是( )
A.(x+1)(1+x) B.(2x-5)(2x+5)
C.(-a+b)(a-b) D.(x2-y)(x+y2)
2.下列运算正确的是( )
A.x7÷x5=x2 B.(xy2)2=xy4
C.x2·x5=x10 D.( + )( - )=b-a
B
A
3.填空:
(1
(2
(3
(4)化简的结果是 .
1-9a2
4y2-9x2
3a
3a
x2-1
4.计算:
(1)2;(2)2 491;(3)1.
5.如图2①所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸片拼成如图2②所示的等腰梯形.
(1)设图①中阴影部分面积为S1,图②中阴影部分面积为S2,请直接用含a,b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
6.如图所示,小明家有一块“L”形的自留地,现在要分成两块形状、面积相同的部分,种上两种不同的蔬菜,请你来帮小明设计,并算出这块自留地的面积.
7.(选做题)(吉林中考)某同学化简出现了错误,解答过程如下:
原式=第一步)
=(第二步)
=(第三步)
(1)该同学解答过程从第 步开始出错,错误原因是 ;
(2)写出此题正确的解答过程.
解:(1)二 去括号时有一项没有变号
(2)原式 =
课堂小结
平方差公式
(a+b)(a- b)=
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
