19.3矩形、菱形、正方形(第1课时矩形的定义与性质) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.3矩形、菱形、正方形(第1课时矩形的定义与性质) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览






文档简介
(共23张PPT)
19.3 矩形、菱形、正方形
第1课时 矩形的定义与性质
第19章 四边形
学 习 目 标
2
3
探索并掌握“直角三角形斜边上的中线等于斜边的一半”这个定理.(重点)
理解矩形的概念,明确矩形与平行四边形的区别与联系.
1
探索并证明矩形的性质,会用矩形的性质解决简单的问题.(重点)
新课导入
1.平行四边形的定义?平行四边形的性质?
2.问题1:在观察图片后,你能从中发现你熟悉的图形吗?
你认为它们有什么样的共同特征呢?
问题2:请同学们观察,彩图中的平行四边形与?ABCD相比较,还有不同点吗?
结论:这些平行四边形中有一个角是直角
预习新知
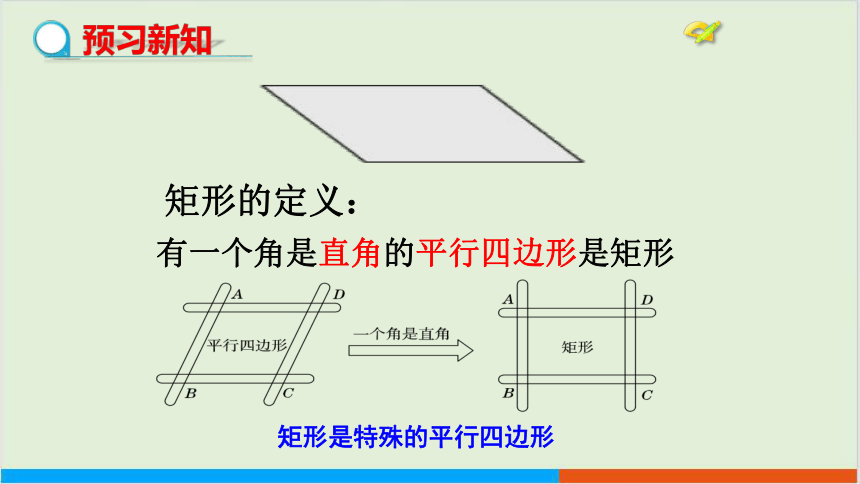
有一个角是直角的平行四边形是矩形
矩形的定义:
矩形是特殊的平行四边形
知识讲解
探究活动一:矩形四角的大小关系
矩形的四个角都是直角.
问题2:既然它具有平行四边形的所有性质,那么矩形是否具有它独特的性质呢?
已知:矩形ABCD.如图:
求证:∠A=∠B=∠C=∠D.
证明:由定义知,矩形必有一个角是直角,设∠A=90°.
D
A
B
C
∵AB∥DC, AD∥BC,
∴∠B =∠C=∠D=90°.(两直线平行,同旁内角互补)
即矩形ABCD的四个角都是直角.
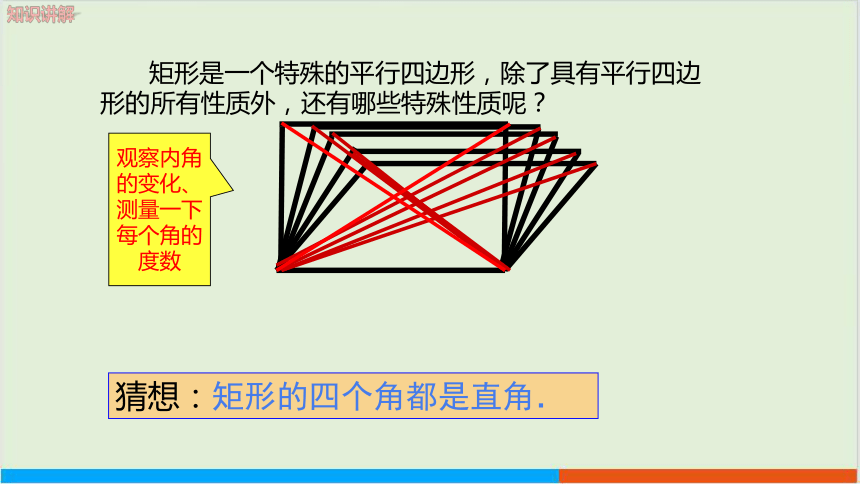
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想:矩形的四个角都是直角.
观察内角的变化、测量一下每个角的度数
证明猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,
∠A +∠B = 180°,
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
探究活动二:对角线的数量关系
学生用橡皮筋做出两条对角线,让学生观察这两条对角线的关系?
结论:矩形的两条对角线相等.
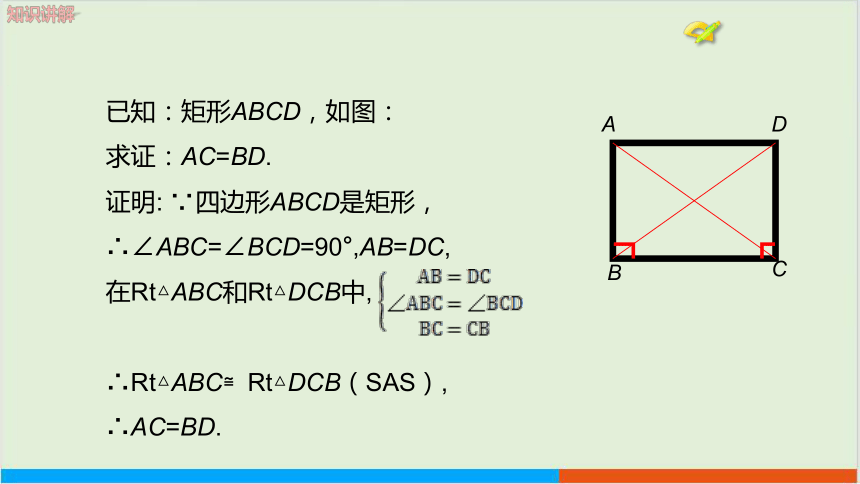
已知:矩形ABCD,如图:
求证:AC=BD.
证明: ∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,AB=DC,
在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(SAS),
∴AC=BD.
A
B
C
D
探究活动三:直角三角形中斜边上的中线与斜边的数量关系
如图:矩形ABCD中,AO=_____AC,BO=______BD.BO是Rt△ABC的什么线?由此你可以得到什么结论?
A
B
C
D
O
结论:直角三角形斜边上的中线等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
∵ AC=BD,BO=DO,
∴ BO= BD,BO= AC.
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形的一般性质:
例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长.
∴ AC=BD,∴ OA=OB.
∵ ∠AOB=120°,
在Rt△ABD中,BD=2AD=8 cm.
∴ 矩形的对角线长 8㎝.
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
∴∠OAB=∠OBA=
=30°.
A
B
C
D
E
F
O
如图,在矩形ABCD中,AC、BD交于点O,点E、点F分别在AO、DO上,且∠EBO=∠FCO.
(1)求证:EO=FO;
(2)若∠EBO=∠ACB=30°,BC=
,求△BEO的面积.
练一练
A
B
C
D
E
F
O
(1)证明:∵四边形ABCD是矩形,
∴OB= BD,OC= AC,且AC=BD,
∴OB=OC,
在△EBO和△FCO中,
∵ ,
∴△EBO≌△FCO(ASA),
∴OE=OF;
A
B
C
D
E
F
O
(2)解:∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠ACB=30°,
∴∠OBC=30°,
∴∠BEC=180°﹣30°﹣30°﹣30°=90°,
∵BC= ,
∴BE= BC= ,
Rt△BEO中,∵∠EBO=30°,
∴OE=1,
.
∴△BEO的面积=
随堂训练
1、矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
2. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
D
3.如图:已知:在矩形ABCD中,对角线AC与BD相交于O,∠ ACB=30°,AB=5㎝,则AC= ㎝,BD= ㎝.
10
10
4.如图,在矩形ABCD中,点E,F在对角线BD上.请添加一个条件,使得结论“AE=CF ”成立,并加以证明.
解:添加条件:BE=DF(或DE=BF或AE∥CF或∠AEB=∠DFC或∠DAE=∠BCF或∠AED=∠CFB或∠BAE=∠DCF等).
选择BE=DF.
证明:在矩形ABCD中,AB∥CD,AB=CD,
∴ ∠ABE=∠CDF.
∵ BE=DF,∴ △ABE≌△CDF(SAS).
∴ AE=CF.
5.如图,在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE于F.
(1)求证:AE=BC;
(2)如果AB=3,AF=4,求EC的长.
A
B
C
D
E
F
A
B
C
D
E
F
(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∵DF=DC,
∴AB=DF,
在△ABE和△DFA中 ,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∴AE=BC;
(2)解:由(1)得:△ABE≌△DFA,
∴BE=AF=4,AE=BC,
∵∠B=90°,
∴AE= = =5,
∴BC=5,
∴EC=BC﹣BE=5﹣4=1.
课堂小结
直角三角形斜边上的中线等于斜边的一半.
矩形:有一个角是直角的平行四边形叫做矩形.
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
矩
形
的
性
质
19.3 矩形、菱形、正方形
第1课时 矩形的定义与性质
第19章 四边形
学 习 目 标
2
3
探索并掌握“直角三角形斜边上的中线等于斜边的一半”这个定理.(重点)
理解矩形的概念,明确矩形与平行四边形的区别与联系.
1
探索并证明矩形的性质,会用矩形的性质解决简单的问题.(重点)
新课导入
1.平行四边形的定义?平行四边形的性质?
2.问题1:在观察图片后,你能从中发现你熟悉的图形吗?
你认为它们有什么样的共同特征呢?
问题2:请同学们观察,彩图中的平行四边形与?ABCD相比较,还有不同点吗?
结论:这些平行四边形中有一个角是直角
预习新知
有一个角是直角的平行四边形是矩形
矩形的定义:
矩形是特殊的平行四边形
知识讲解
探究活动一:矩形四角的大小关系
矩形的四个角都是直角.
问题2:既然它具有平行四边形的所有性质,那么矩形是否具有它独特的性质呢?
已知:矩形ABCD.如图:
求证:∠A=∠B=∠C=∠D.
证明:由定义知,矩形必有一个角是直角,设∠A=90°.
D
A
B
C
∵AB∥DC, AD∥BC,
∴∠B =∠C=∠D=90°.(两直线平行,同旁内角互补)
即矩形ABCD的四个角都是直角.
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想:矩形的四个角都是直角.
观察内角的变化、测量一下每个角的度数
证明猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形.
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又矩形ABCD是平行四边形,
∴ ∠A=∠C , ∠B = ∠D,
∠A +∠B = 180°,
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
探究活动二:对角线的数量关系
学生用橡皮筋做出两条对角线,让学生观察这两条对角线的关系?
结论:矩形的两条对角线相等.
已知:矩形ABCD,如图:
求证:AC=BD.
证明: ∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,AB=DC,
在Rt△ABC和Rt△DCB中,
∴Rt△ABC≌Rt△DCB(SAS),
∴AC=BD.
A
B
C
D
探究活动三:直角三角形中斜边上的中线与斜边的数量关系
如图:矩形ABCD中,AO=_____AC,BO=______BD.BO是Rt△ABC的什么线?由此你可以得到什么结论?
A
B
C
D
O
结论:直角三角形斜边上的中线等于斜边的一半.
BO是Rt△ABC中斜边AC上的中线.
BO等于AC的一半.
∵ AC=BD,BO=DO,
∴ BO= BD,BO= AC.
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形的一般性质:
例 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长.
∴ AC=BD,∴ OA=OB.
∵ ∠AOB=120°,
在Rt△ABD中,BD=2AD=8 cm.
∴ 矩形的对角线长 8㎝.
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
∴∠OAB=∠OBA=
=30°.
A
B
C
D
E
F
O
如图,在矩形ABCD中,AC、BD交于点O,点E、点F分别在AO、DO上,且∠EBO=∠FCO.
(1)求证:EO=FO;
(2)若∠EBO=∠ACB=30°,BC=
,求△BEO的面积.
练一练
A
B
C
D
E
F
O
(1)证明:∵四边形ABCD是矩形,
∴OB= BD,OC= AC,且AC=BD,
∴OB=OC,
在△EBO和△FCO中,
∵ ,
∴△EBO≌△FCO(ASA),
∴OE=OF;
A
B
C
D
E
F
O
(2)解:∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠ACB=30°,
∴∠OBC=30°,
∴∠BEC=180°﹣30°﹣30°﹣30°=90°,
∵BC= ,
∴BE= BC= ,
Rt△BEO中,∵∠EBO=30°,
∴OE=1,
.
∴△BEO的面积=
随堂训练
1、矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
C
2. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为 ( )
A.50° B.60° C.70° D.80°
D
3.如图:已知:在矩形ABCD中,对角线AC与BD相交于O,∠ ACB=30°,AB=5㎝,则AC= ㎝,BD= ㎝.
10
10
4.如图,在矩形ABCD中,点E,F在对角线BD上.请添加一个条件,使得结论“AE=CF ”成立,并加以证明.
解:添加条件:BE=DF(或DE=BF或AE∥CF或∠AEB=∠DFC或∠DAE=∠BCF或∠AED=∠CFB或∠BAE=∠DCF等).
选择BE=DF.
证明:在矩形ABCD中,AB∥CD,AB=CD,
∴ ∠ABE=∠CDF.
∵ BE=DF,∴ △ABE≌△CDF(SAS).
∴ AE=CF.
5.如图,在矩形ABCD中,点E是BC上一点,DF=DC,DF⊥AE于F.
(1)求证:AE=BC;
(2)如果AB=3,AF=4,求EC的长.
A
B
C
D
E
F
A
B
C
D
E
F
(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,AB=DC,AD=BC,AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∵DF=DC,
∴AB=DF,
在△ABE和△DFA中 ,
∴△ABE≌△DFA(AAS),
∴AE=AD,
∴AE=BC;
(2)解:由(1)得:△ABE≌△DFA,
∴BE=AF=4,AE=BC,
∵∠B=90°,
∴AE= = =5,
∴BC=5,
∴EC=BC﹣BE=5﹣4=1.
课堂小结
直角三角形斜边上的中线等于斜边的一半.
矩形:有一个角是直角的平行四边形叫做矩形.
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
矩
形
的
性
质
