19.3矩形、菱形、正方形(第5课时正方形) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 19.3矩形、菱形、正方形(第5课时正方形) 教学课件 沪科版初中数学八年级(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览






文档简介
(共21张PPT)
19.3矩形、菱形、正方形
第5课时 正方形
第19章 四边形
学 习 目 标
2
理解正方形的概念及相关性质;
探索并证明正方形的性质,并了解平行四边形、矩形、菱形之间的联系和区别;(重点)
掌握正方形的判定定理,并会解决相关问题;(难点)
进一步体会证明的必要性以及计算与证明在解决问题中的作用.
1
3
4
知识讲解
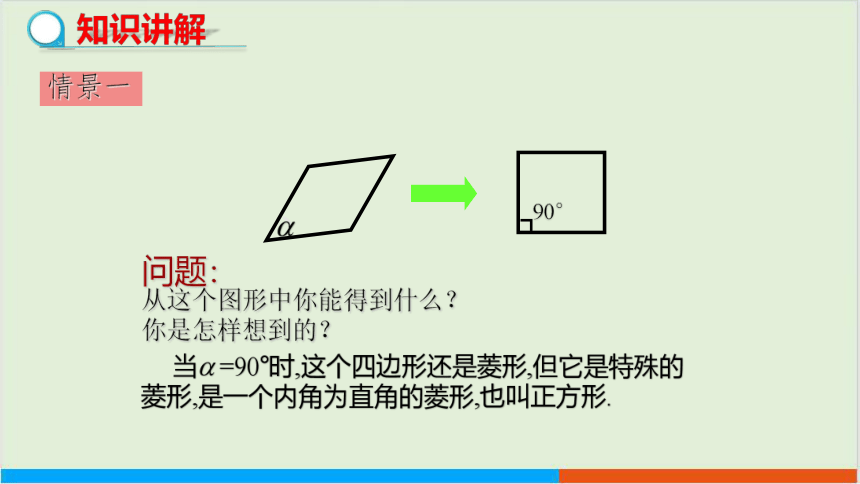
情景一
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
情景二
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
1.正方形的定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
2.(学生动手操作,教师引导)准备一张正方形纸片,折一折,观察并思考:正方形是不是轴对称图形 如果是,那么对称轴有几条
【结论】正方形是轴对称图形,对称轴有4条.
3.继续观察思考:正方形有哪些性质?
(1)正方形的四个角都是直角,四条边相等.
(2)正方形的对角线相等且互相垂直平分.
探究一 正方形性质
性质1:正方形的边角性质
如图,四边形ABCD是正方形.
求证:正方形ABCD四条边相等,四个角都是直角.
证明:∵ 四边形ABCD是正方形,
∴ ∠A=90°, AB=BC.(正方形的定义)
又∵ 正方形是平行四边形,
∴ 四边形ABCD是矩形,(矩形的定义)
四边形ABCD是菱形.(菱形的定义)
∴ ∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
性质2:正方形对角线性质
如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴ AO=BO=CO=DO.
∵ 正方形ABCD是菱形.
∴ AC⊥BD.
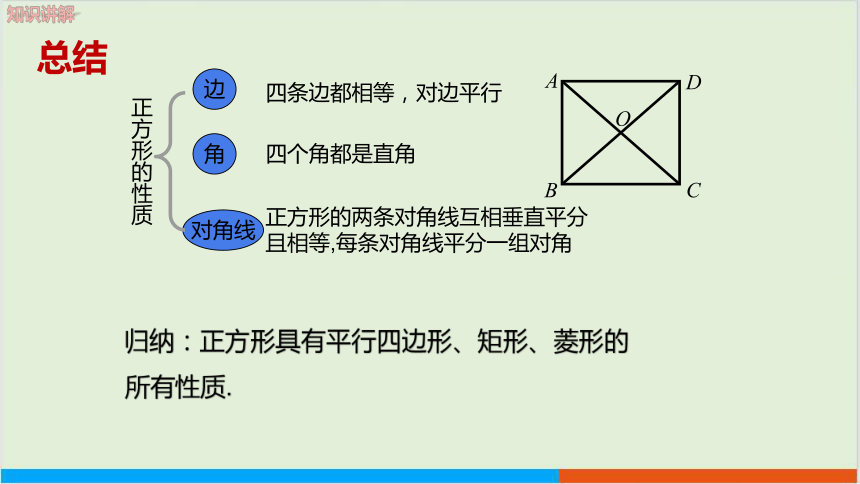
正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角
四条边都相等,对边平行
四个角都是直角
边
对角线
角
正方形的性质
O
A
B
C
D
归纳:正方形具有平行四边形、矩形、菱形的所有性质.
总结
平行四边形
矩形
菱形
正
方
形
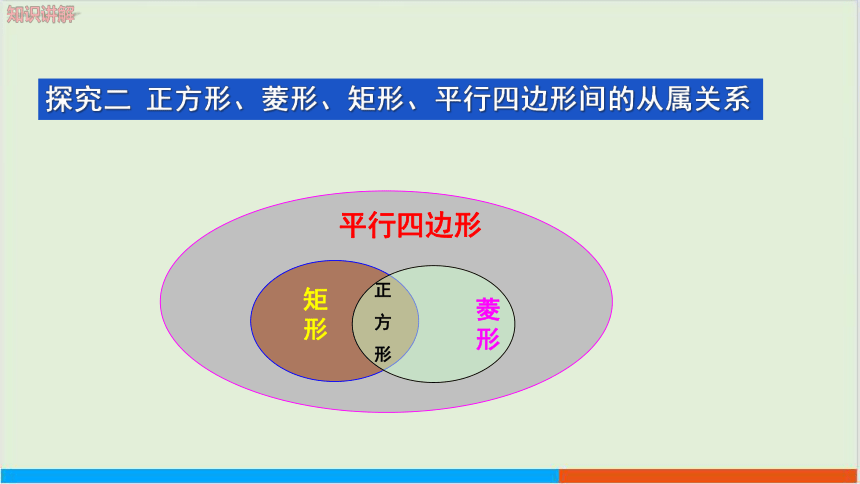
探究二 正方形、菱形、矩形、平行四边形间的从属关系
矩 形
〃
〃
正方形
邻边
相等
〃
〃
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形是正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
探究三 正方形判定
例1 如图,在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF,则BE与DF之间有怎样的关系?请说明理由.
分析:两线段的关系包含着数量关系和位置关系,根据正方形的性质可得BC=DC,∠BCE=∠DCF=90°,然后利用“边角边”证明△BCE和△DCF全等,得出BE=DF.延长BE交DF于点M,进而求出∠CBE+∠F=90°,从而证得BE⊥DF.
M
解:BE=DF,且BE⊥DF.理由如下:
∵ 四边形ABCD是正方形,
∴ BC=DC,∠BCE=90°.(正方形的四条边相等,四个角都是直角)
∴ ∠DCF=180°-∠BCE=180°-90°=90°.
∴ ∠BCE=∠DCF.
又∵ CE=CF,
∴ △BCE≌△DCF,
∴ BE=DF.
延长BE交DF于点M(如图所示),
∵ △BCE≌△DCF ,
∴ ∠CBE=∠CDF.
∵ ∠DCF =90°,
∴ ∠CDF +∠F =90°.
∴ ∠CBE+∠F=90°,
∴ ∠BMF=90°.
∴ BE⊥DF.
如图,在正方形ABCD中,△BCE是等边三角形,求证:∠EAD=∠EDA=15°.
证明:∵ △BCE是等边三角形,
∴ BE=CE=BC,∠EBC=∠ECB=60°.
∵ 四边形ABCD是正方形,
∴ AB=BC=CD,∠ABC=∠DCB=90°.
∴ AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴ △ABE,△DCE是等腰三角形.
∴ ∠BAE=∠BEA=∠CDE=∠CED= (180°-30°)=75°,
∴ ∠EAD=∠EDA=90°-75°=15°.
练一练
例2 如图,A′,B′,C′,D′分别是正方形ABCD四条边上的点,且A A′=B B′=C C′=D D′.求证:四边形A′B′C′D′是正方形.
D ′
D
A
B
C
A ′
C ′
B ′
2
3
1
证明: ∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
又∵A A′=B B′=C C′=D D′,
∴D′A = A′B = B′C = C′D
∵∠A=∠B=∠C=∠D=90°.
∴△AA′D≌△BB′A′≌△CC′B′≌△DD′C′.
∴A′B′=B′C′=C′D′=D′A.
∴四边形A′B′C′D′是菱形.
又∵∠1=∠3,∠1+∠2=90°,
∴∠2+∠3=90°
∴∠D′A′B′=90°.
所以四边形A′B′C′D′是正方形.
如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
解:∵ BF∥CE,CF∥BE,
∴ 四边形BECF是平行四边形.
又∵ 在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,
∴ ∠EBC=∠ECB=45°,
∴ BE=CE,∠BEC=90°,
∴ 四边形BECF是菱形.
又∵ ∠BEC=90°,
∴ 四边形BECF是正方形.
练一练
随堂训练
112.5 °
A
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
2.如图,在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
5
30°
3.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
5.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.
求证:四边形DFCE是正方形.
A
B
C
D
E
F
证明:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
6.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵ 四边形ABCD为正方形,
∴ ∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵ EF⊥AC,
∴ ∠EFA=∠EFC=90°.
又∵ ∠ECF=45°,∴ △EFC是等腰直角三角形,
∴ EF=FC.
∵ ∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴ △ABE≌△AFE,
∴ AB=AF=1cm,BE=FE,∴ FC=BE.
在Rt△ABC中,由勾股定理得
∴ FC=AC-AF=(
-1)cm,
-1)cm.
∴ BE=(
课堂小结
19.3矩形、菱形、正方形
第5课时 正方形
第19章 四边形
学 习 目 标
2
理解正方形的概念及相关性质;
探索并证明正方形的性质,并了解平行四边形、矩形、菱形之间的联系和区别;(重点)
掌握正方形的判定定理,并会解决相关问题;(难点)
进一步体会证明的必要性以及计算与证明在解决问题中的作用.
1
3
4
知识讲解
情景一
问题:
从这个图形中你能得到什么?
你是怎样想到的?
┓
90°
当 =90°时,这个四边形还是菱形,但它是特殊的菱形,是一个内角为直角的菱形,也叫正方形.
问题:
情景二
1.图中CD在移动时,这个图形始终是怎样的图形?(CD在移动的过程中始终保持与AB平行)
2.当CD移动到C D 位置,且 AD =AB时,此时的图形还是矩形吗?
A
B
C
D
A
B
C
D
当AD=AB时,这个四边形是矩形,它是特殊的矩形,是一组邻边相等的矩形,也叫正方形.
1.正方形的定义:有一个角是直角,且有一组邻边相等的平行四边形叫做正方形.
2.(学生动手操作,教师引导)准备一张正方形纸片,折一折,观察并思考:正方形是不是轴对称图形 如果是,那么对称轴有几条
【结论】正方形是轴对称图形,对称轴有4条.
3.继续观察思考:正方形有哪些性质?
(1)正方形的四个角都是直角,四条边相等.
(2)正方形的对角线相等且互相垂直平分.
探究一 正方形性质
性质1:正方形的边角性质
如图,四边形ABCD是正方形.
求证:正方形ABCD四条边相等,四个角都是直角.
证明:∵ 四边形ABCD是正方形,
∴ ∠A=90°, AB=BC.(正方形的定义)
又∵ 正方形是平行四边形,
∴ 四边形ABCD是矩形,(矩形的定义)
四边形ABCD是菱形.(菱形的定义)
∴ ∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
性质2:正方形对角线性质
如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:AO=BO=CO=DO,AC⊥BD.
证明:∵正方形ABCD是矩形,
∴ AO=BO=CO=DO.
∵ 正方形ABCD是菱形.
∴ AC⊥BD.
正方形的两条对角线互相垂直平分且相等,每条对角线平分一组对角
四条边都相等,对边平行
四个角都是直角
边
对角线
角
正方形的性质
O
A
B
C
D
归纳:正方形具有平行四边形、矩形、菱形的所有性质.
总结
平行四边形
矩形
菱形
正
方
形
探究二 正方形、菱形、矩形、平行四边形间的从属关系
矩 形
〃
〃
正方形
邻边
相等
〃
〃
一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
一个角为直角的菱形是正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形是正方形.
探究三 正方形判定
例1 如图,在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF,则BE与DF之间有怎样的关系?请说明理由.
分析:两线段的关系包含着数量关系和位置关系,根据正方形的性质可得BC=DC,∠BCE=∠DCF=90°,然后利用“边角边”证明△BCE和△DCF全等,得出BE=DF.延长BE交DF于点M,进而求出∠CBE+∠F=90°,从而证得BE⊥DF.
M
解:BE=DF,且BE⊥DF.理由如下:
∵ 四边形ABCD是正方形,
∴ BC=DC,∠BCE=90°.(正方形的四条边相等,四个角都是直角)
∴ ∠DCF=180°-∠BCE=180°-90°=90°.
∴ ∠BCE=∠DCF.
又∵ CE=CF,
∴ △BCE≌△DCF,
∴ BE=DF.
延长BE交DF于点M(如图所示),
∵ △BCE≌△DCF ,
∴ ∠CBE=∠CDF.
∵ ∠DCF =90°,
∴ ∠CDF +∠F =90°.
∴ ∠CBE+∠F=90°,
∴ ∠BMF=90°.
∴ BE⊥DF.
如图,在正方形ABCD中,△BCE是等边三角形,求证:∠EAD=∠EDA=15°.
证明:∵ △BCE是等边三角形,
∴ BE=CE=BC,∠EBC=∠ECB=60°.
∵ 四边形ABCD是正方形,
∴ AB=BC=CD,∠ABC=∠DCB=90°.
∴ AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴ △ABE,△DCE是等腰三角形.
∴ ∠BAE=∠BEA=∠CDE=∠CED= (180°-30°)=75°,
∴ ∠EAD=∠EDA=90°-75°=15°.
练一练
例2 如图,A′,B′,C′,D′分别是正方形ABCD四条边上的点,且A A′=B B′=C C′=D D′.求证:四边形A′B′C′D′是正方形.
D ′
D
A
B
C
A ′
C ′
B ′
2
3
1
证明: ∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
又∵A A′=B B′=C C′=D D′,
∴D′A = A′B = B′C = C′D
∵∠A=∠B=∠C=∠D=90°.
∴△AA′D≌△BB′A′≌△CC′B′≌△DD′C′.
∴A′B′=B′C′=C′D′=D′A.
∴四边形A′B′C′D′是菱形.
又∵∠1=∠3,∠1+∠2=90°,
∴∠2+∠3=90°
∴∠D′A′B′=90°.
所以四边形A′B′C′D′是正方形.
如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
解:∵ BF∥CE,CF∥BE,
∴ 四边形BECF是平行四边形.
又∵ 在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,
∴ ∠EBC=∠ECB=45°,
∴ BE=CE,∠BEC=90°,
∴ 四边形BECF是菱形.
又∵ ∠BEC=90°,
∴ 四边形BECF是正方形.
练一练
随堂训练
112.5 °
A
1.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
2.如图,在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
4.已知正方形ABCD中,AC=10,P是AB上一点,
PE⊥AC于E,PF⊥BD于F,则PE+PF=____.
5
30°
3.以正方形ABCD的边DC向外作等边△DCE,
则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
5.如图,四边形ABCD是正方形,对角线AC、BD相交于点F,∠E=90°,ED=EC.
求证:四边形DFCE是正方形.
A
B
C
D
E
F
证明:∵四边形ABCD是正方形,
∴∠FDC=∠DCF=45°,
∵∠E=90°,ED=EC,
∴∠EDC=∠ECD=45°,
∴∠FCE=∠FDE=∠E=90°,
∴四边形DFCE是矩形,
∵DE=CE,
∴四边形DFCE是正方形.
6.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵ 四边形ABCD为正方形,
∴ ∠B=90°,∠ACB=45°,AB=BC=1 cm.
∵ EF⊥AC,
∴ ∠EFA=∠EFC=90°.
又∵ ∠ECF=45°,∴ △EFC是等腰直角三角形,
∴ EF=FC.
∵ ∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴ △ABE≌△AFE,
∴ AB=AF=1cm,BE=FE,∴ FC=BE.
在Rt△ABC中,由勾股定理得
∴ FC=AC-AF=(
-1)cm,
-1)cm.
∴ BE=(
课堂小结
