20.1数据的频数分布 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 20.1数据的频数分布 教学课件 沪科版初中数学八年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览








文档简介
(共28张PPT)
20.1 数据的频数分布
第20 章 数据的初步分析
1
2
学习目标
了解频数、频率和频数分布的意义.
能画频数直方图,能初步把数字信息、图形和语言之间相互转化,能根据统计结果做出合理的判断和预测.(重点、难点)
在具体情境中感受统计图表与现实生活的密切联系,进一步树立数据分析的观念.
3
温故知新
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
知识讲解
某校学生在假期进行“空气质量情况调查”的课题研究时,他们从当地气象部门提供的今年上半年的资料中,随机抽取了30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
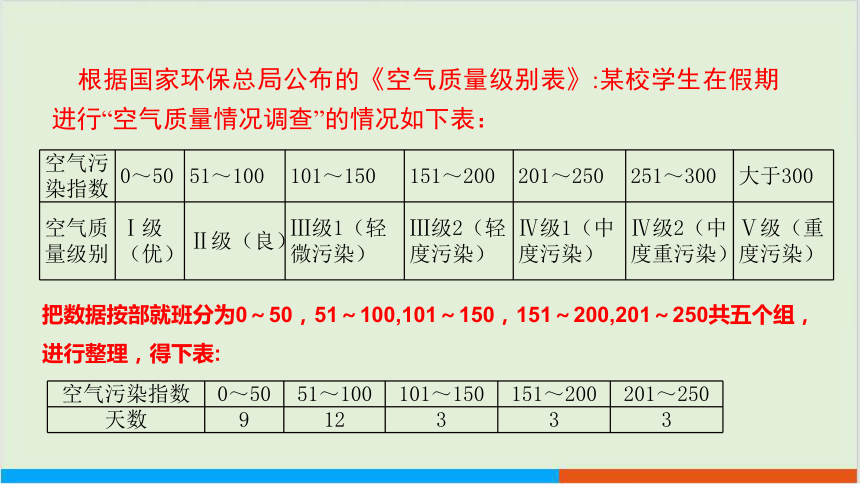
根据国家环保总局公布的《空气质量级别表》:某校学生在假期进行“空气质量情况调查”的情况如下表:
把数据按部就班分为0~50,51~100,101~150,151~200,201~250共五个组,进行整理,得下表:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级(优) Ⅱ级(良) Ⅲ级1(轻微污染) Ⅲ级2(轻度污染) Ⅳ级1(中度污染) Ⅳ级2(中度重污染) Ⅴ级(重度污染)
空气污染指数 0~50 51~100 101~150 151~200 201~250
天数 9 12 3 3 3
思考:从表格中你能得到什么信息?
1.说明这30天的空气质量,根据国家公布的级别,各占绝大多数比率(即分布情况).
2.这名学生估计该地今年(按365天算)空气质量达到优级别的天数约是110天.
在上面的数据中,最小值是17,最大值是62,它们的差是62-15=47,说明平均每天参加课外锻炼的时间范围是47.
一、计算最大值和最小值的差
为了解全体学生一周内平均每天参加课外锻炼的时间,你知道怎样做才能知道数据(身高)的分布情况?
二、决定组距和组数
所以要将数据分成6组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为6和8.
组距是指每个小组的两个端点间的距离,根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
将这批数据分组.如果每组组距相同,并取组距为8,那么
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
三、决定分点
所以要将数据分成6组:14.5~22.5,22.5~30.5,30.5~38.5,
38.5~46.5,46.5~54.5,54.5~62.5.这里组数和组距分别为6和8.
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
注意:有些数不好决定它们的属于那一组,所以我们把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
1.频数:我们把一批数据中落在某个小组内数据的个数称为这个组的频数.
2.频数分布表:通常用选举时唱票的方法,对落在各个小组内的数据个数进行记录,算出每一个小组的频数,并制成频数分布表
3.频率:如果一批数据共有n个,而其中某一组数据是m个.那么m/n就是该组数据在这批数据中出现的频率.
四、列频数分布表
四、列频数分布表
40名学生平均每天锻炼时间频数分布表
分组 频数统计 频数
14.5~22.5
22.5~30.5
30.5~38.5
38.5~46.5
46.5~54.5
54.5~62.5
合计
正正
正正正
正
2
3
10
19
5
1
40
探究
上面我们选取的组距是6,从而把数据分成8组,如果组距取4,那么数据分成几个组?那种分组方法更合适呢?
五、画频数分布直方图
画出相互垂直的两条直线,用横轴表示分组情况,纵轴表示频数,绘出相应的长方形条,就得到了频数直方图.
40名学生平均每天锻炼时间频数分布表”绘制的直方图:
讨论
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
归纳
制作频数分布直方图的一般步骤是什么?
(1)计算这批数据中最大数与最小数的差.
(5)画频数直方图.
(4)列频数分布表.
(2)决定组距和组数
(3)决定分点.
例题讲解
例 某校从七年级中任意抽取一个班,该班级学位高 (单位:cm)的频数分布如所示:
分组 136.5~ 141.5 141.5~ 146.5 146.5~ 151.5 151.5~ 156.5 156.5~ 161.5 161.5~ 171.5 166.5~ 171.5 171.5~ 176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5厘米以上的学生有多少人?占全班人数的百分之百呢?
(2)估计该校七年级全体400名新生中,身高在161.5cm以上的约有多少人
解 :(1)身高在161.5cm以上的学生有
8+2+1=11(人),
占全班人数的22%.
(2)全体七年级学生中,身高在161.5cm以上的人数
约为 400×22%=88(人).
跟踪训练
为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差 7.4-4.0=3.4,
(2)决定组距和组数
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
(3)决定分点
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点,那么,所分的12个小组可以是:
3.95~4.25,4.25~4.55,4.55~4.85 ,4.85~5.15,5.15~5.45,5.45~5.75,5.75~6.05,6.05~6.35,6.35~6.65,6.65~6.95,6.95~7.25,7.25~7.55.
(4)列频数分布表
分组 频数 频率
3.95~4.25 1 0.01
4.25~4.55 1 0.01
4.55~4.85 2 0.02
4.85~5.15 5 0.05
5.15~5.45 11 0.11
5.45~5.75 15 0.15
5.75~6.05 28 0.28
6.05~6.35 13 0.13
6.35~6.65 11 0.11
6.65~6.95 10 0.10
6.95~7.25 2 0.02
7.25~7.55 1 0.01
合计 100 1
(5)画频数分布直方图
从表和图中看到,长度在5.75~6.05厘米的麦穗所占的比最大,达到28%,而长度在3.95~4.25、4.25~4.55、4.55~4.85、6.95~7.25、7.25~7.55等范围内的麦穗所占的比的和只有7%.
随堂训练
1.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1 000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
解析:由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-8-24-30-10=28,占抽查学生的比例为28÷100×100%=28%.采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280.
2.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有( )
A.6人
B.8人
C.16人
D.20人
D
解析:从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,即各组频数之比为1∶4∶3∶2.一分钟跳绳次数在100次以上的即第三、四组,所占比例为.故有40×20(人).
3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则下列说法:① 该班有50名同学参赛;② 第五组的百分比为16%;③ 成绩在70~80分的人数最多;④ 80分以上的学生有14名,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
解析:第五组所占的百分比是14%12%40%28%16%,故②正确;
该班参赛学生数是8÷16%50(名),故①正确;
从直方图可以直接看出成绩在70~80分的人数最多,故③正确;
80分以上的学生有50×(28%16%)22(名),故④错误.
其中正确的有①②③,共3个.
4、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 .
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课堂小结
制作频数分布直方图
1.计算最大值与最小值的差
2.决定组数和组距
4.列频数分布表
5.绘制频数直方图
3.决定分点并分组
20.1 数据的频数分布
第20 章 数据的初步分析
1
2
学习目标
了解频数、频率和频数分布的意义.
能画频数直方图,能初步把数字信息、图形和语言之间相互转化,能根据统计结果做出合理的判断和预测.(重点、难点)
在具体情境中感受统计图表与现实生活的密切联系,进一步树立数据分析的观念.
3
温故知新
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
知识讲解
某校学生在假期进行“空气质量情况调查”的课题研究时,他们从当地气象部门提供的今年上半年的资料中,随机抽取了30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
根据国家环保总局公布的《空气质量级别表》:某校学生在假期进行“空气质量情况调查”的情况如下表:
把数据按部就班分为0~50,51~100,101~150,151~200,201~250共五个组,进行整理,得下表:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级(优) Ⅱ级(良) Ⅲ级1(轻微污染) Ⅲ级2(轻度污染) Ⅳ级1(中度污染) Ⅳ级2(中度重污染) Ⅴ级(重度污染)
空气污染指数 0~50 51~100 101~150 151~200 201~250
天数 9 12 3 3 3
思考:从表格中你能得到什么信息?
1.说明这30天的空气质量,根据国家公布的级别,各占绝大多数比率(即分布情况).
2.这名学生估计该地今年(按365天算)空气质量达到优级别的天数约是110天.
在上面的数据中,最小值是17,最大值是62,它们的差是62-15=47,说明平均每天参加课外锻炼的时间范围是47.
一、计算最大值和最小值的差
为了解全体学生一周内平均每天参加课外锻炼的时间,你知道怎样做才能知道数据(身高)的分布情况?
二、决定组距和组数
所以要将数据分成6组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别为6和8.
组距是指每个小组的两个端点间的距离,根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
将这批数据分组.如果每组组距相同,并取组距为8,那么
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
三、决定分点
所以要将数据分成6组:14.5~22.5,22.5~30.5,30.5~38.5,
38.5~46.5,46.5~54.5,54.5~62.5.这里组数和组距分别为6和8.
组距和组数的确定没有固定的标准,要凭借经验和所研究的具体问题来决定.
注意:有些数不好决定它们的属于那一组,所以我们把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
1.频数:我们把一批数据中落在某个小组内数据的个数称为这个组的频数.
2.频数分布表:通常用选举时唱票的方法,对落在各个小组内的数据个数进行记录,算出每一个小组的频数,并制成频数分布表
3.频率:如果一批数据共有n个,而其中某一组数据是m个.那么m/n就是该组数据在这批数据中出现的频率.
四、列频数分布表
四、列频数分布表
40名学生平均每天锻炼时间频数分布表
分组 频数统计 频数
14.5~22.5
22.5~30.5
30.5~38.5
38.5~46.5
46.5~54.5
54.5~62.5
合计
正正
正正正
正
2
3
10
19
5
1
40
探究
上面我们选取的组距是6,从而把数据分成8组,如果组距取4,那么数据分成几个组?那种分组方法更合适呢?
五、画频数分布直方图
画出相互垂直的两条直线,用横轴表示分组情况,纵轴表示频数,绘出相应的长方形条,就得到了频数直方图.
40名学生平均每天锻炼时间频数分布表”绘制的直方图:
讨论
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
归纳
制作频数分布直方图的一般步骤是什么?
(1)计算这批数据中最大数与最小数的差.
(5)画频数直方图.
(4)列频数分布表.
(2)决定组距和组数
(3)决定分点.
例题讲解
例 某校从七年级中任意抽取一个班,该班级学位高 (单位:cm)的频数分布如所示:
分组 136.5~ 141.5 141.5~ 146.5 146.5~ 151.5 151.5~ 156.5 156.5~ 161.5 161.5~ 171.5 166.5~ 171.5 171.5~ 176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5厘米以上的学生有多少人?占全班人数的百分之百呢?
(2)估计该校七年级全体400名新生中,身高在161.5cm以上的约有多少人
解 :(1)身高在161.5cm以上的学生有
8+2+1=11(人),
占全班人数的22%.
(2)全体七年级学生中,身高在161.5cm以上的人数
约为 400×22%=88(人).
跟踪训练
为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差 7.4-4.0=3.4,
(2)决定组距和组数
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
(3)决定分点
使分点比数据多一位小数,并且把第1小组的起点稍微减小一点,那么,所分的12个小组可以是:
3.95~4.25,4.25~4.55,4.55~4.85 ,4.85~5.15,5.15~5.45,5.45~5.75,5.75~6.05,6.05~6.35,6.35~6.65,6.65~6.95,6.95~7.25,7.25~7.55.
(4)列频数分布表
分组 频数 频率
3.95~4.25 1 0.01
4.25~4.55 1 0.01
4.55~4.85 2 0.02
4.85~5.15 5 0.05
5.15~5.45 11 0.11
5.45~5.75 15 0.15
5.75~6.05 28 0.28
6.05~6.35 13 0.13
6.35~6.65 11 0.11
6.65~6.95 10 0.10
6.95~7.25 2 0.02
7.25~7.55 1 0.01
合计 100 1
(5)画频数分布直方图
从表和图中看到,长度在5.75~6.05厘米的麦穗所占的比最大,达到28%,而长度在3.95~4.25、4.25~4.55、4.55~4.85、6.95~7.25、7.25~7.55等范围内的麦穗所占的比的和只有7%.
随堂训练
1.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1 000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
解析:由频数分布直方图知样本中参加社团活动时间在8~10小时之间的学生数是100-8-24-30-10=28,占抽查学生的比例为28÷100×100%=28%.采用样本估计总体的方法知该校五一期间参加社团活动时间在8~10小时之间的学生数大约是1 000×28%=280.
2.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有( )
A.6人
B.8人
C.16人
D.20人
D
解析:从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,即各组频数之比为1∶4∶3∶2.一分钟跳绳次数在100次以上的即第三、四组,所占比例为.故有40×20(人).
3.某班将安全知识竞赛成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则下列说法:① 该班有50名同学参赛;② 第五组的百分比为16%;③ 成绩在70~80分的人数最多;④ 80分以上的学生有14名,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
解析:第五组所占的百分比是14%12%40%28%16%,故②正确;
该班参赛学生数是8÷16%50(名),故①正确;
从直方图可以直接看出成绩在70~80分的人数最多,故③正确;
80分以上的学生有50×(28%16%)22(名),故④错误.
其中正确的有①②③,共3个.
4、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 .
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课堂小结
制作频数分布直方图
1.计算最大值与最小值的差
2.决定组数和组距
4.列频数分布表
5.绘制频数直方图
3.决定分点并分组
