冀教版数学七年级下·10.4一元一次不等式的应用教学课件
文档属性
| 名称 | 冀教版数学七年级下·10.4一元一次不等式的应用教学课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:22:42 | ||
图片预览





文档简介
(共16张PPT)
第十章 一元一次不等式和一元一次不等式组
第十章 一元一次不等式和
一元一次不等式组
10.4 一元一次不等式的应用
学 习 目 标
1
2
经历“实际问题抽象为不等式模型”的过程,从而学会用一元一次不等式解决实际问题.(重、难点)
体会不等式是刻画现实世界中不等关系的一种有效的数学模型.
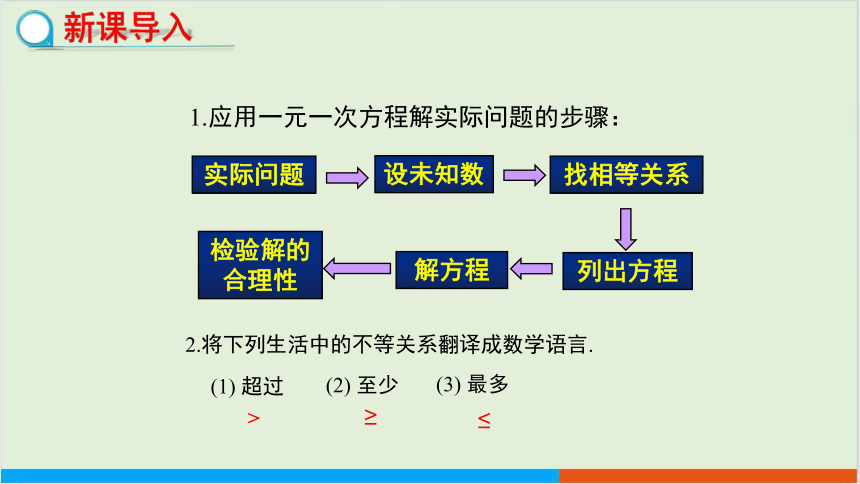
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
新课导入
例:七年级(一)班的学生准备用500元,购买甲、乙两种图书共12套,送给老区的幼儿园小朋友.已知甲种图书每套45元,乙种图书每套40元.这些钱最多能买甲种图书多少套
问题1: 设可购买甲种图书x套,则购买甲种图书用的钱为______元,购买乙种图书________套,购买乙种图书用的钱为________ 元.
45x
(12-x)
40(12-x)
知识讲解
问题2: 购买甲、乙两种图书所用钱数与500元有什么关系
甲图书所用钱数 + 乙图书所用钱数 ≤ 500.
问题3: 你能用不等式把这种关系表示出来吗
45x+40(12-x)≤ 500
问题4:解上面列出的不等式,并根据解集确定实际问题的答案.
解得x≤ 4,故最多购买甲图书4套.
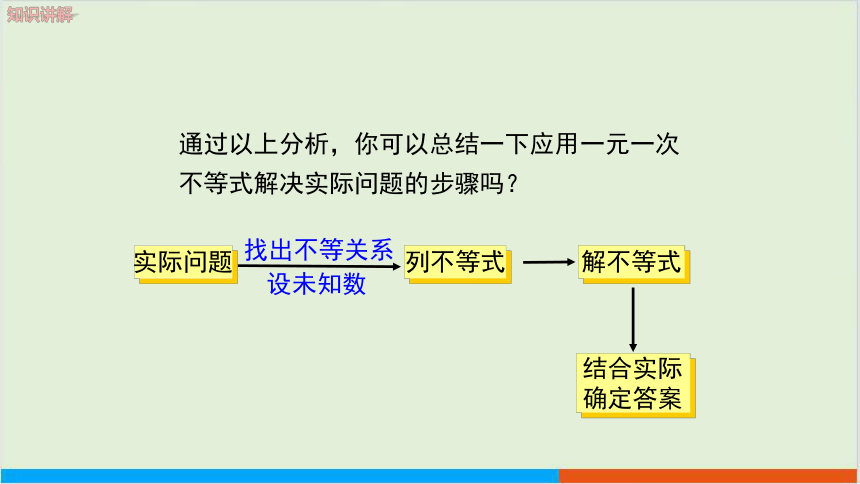
通过以上分析,你可以总结一下应用一元一次不等式解决实际问题的步骤吗?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
例1 某商场决定采购一批电冰箱,优惠销售给农民朋友. 商场从厂家直接购进甲、乙、丙三种不同型号的电冰箱共80台,其中,甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132000元,已知甲、乙、丙三种电冰箱每台的出厂价格分别为1200元,1600元,2000元. 那么该商场购进的乙种电冰箱至少为多少台?
解析:题中的等量关系,
甲冰箱数 + 乙冰箱数 + 丙冰箱数 = 80
甲冰箱数 = 2×乙冰箱数
题中的不等关系,
1200×甲冰箱数+1600×乙冰箱数+
2000×丙冰箱数≤132000
根据题意列不等式,得
1200×2x+1600x+2000(80-3x)≤132000.
解这个不等式,得
x≥14.
答:至少购进乙种电冰箱14台.
解:设购买乙种电冰箱x台,则购买甲种电冰箱是2x台,丙种电冰箱是(80-3x)台.
随 堂 训 练
1.某市天然气公司在居民小区安装天然气管道时采用一种鼓励居民使用天然气的收费方法若整个小区每户都安装收整体初装费10 000元再对每户收费500元.某小区按这种收费方法全部安装天然气后每户平均支付不足1 000元则这个小区的住户数( )
A.至少20户 B.至多20户
C.至少21户 D.至多21户
C
解析:设这个小区的住户数为x户则1 000x10 000.
随堂训练
2.某商品的标价比成本价高m%根据市场需要该商品需降价n%出售为了不亏本n应满足( )
A.n≤m B.n≤ C.n≤ D.n≤
B
解析:设该商品的成本价为a元由题意可得
3.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,根据题意,得
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
随堂训练
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
小琴最多打了5min的电话.
4.某汽车租赁公司要购买轿车和面包车共10辆,其中轿
车至少要购买3辆,轿车每辆7万元,面包车每辆4万
元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由。
(2)如果每辆轿车的日租金为200元,每辆面包车的日租
金为110元,假设新购买的这10辆车每日都可租出,
要使这10辆车的日租金收入不低于1500元,那么应
选择以上哪种购买方案?
解: (1)设轿车要购买x辆,那么面包车要购买(10-x)辆,
7x+4(10-x)≤55,解得 x≤5,
又x≥3,则x=3,4,5,
∴有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2)方案一的日租金为3×200+7×110=1370;
方案二的日租金为:4×200+6×110=1460;
方案三的日租金为:5×200+5×110=1550;
为保证日租金不低于1500,应选方案三.
课 堂 小 结
列一元一次不等式解应用题的一般步骤:
(1)审题,找不等关系;
(2)设未知数,用未知数表示有关代数式
(3)列不等式
(4)解不等式
(5)根据实际情况写出答案
第十章 一元一次不等式和一元一次不等式组
第十章 一元一次不等式和
一元一次不等式组
10.4 一元一次不等式的应用
学 习 目 标
1
2
经历“实际问题抽象为不等式模型”的过程,从而学会用一元一次不等式解决实际问题.(重、难点)
体会不等式是刻画现实世界中不等关系的一种有效的数学模型.
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
新课导入
例:七年级(一)班的学生准备用500元,购买甲、乙两种图书共12套,送给老区的幼儿园小朋友.已知甲种图书每套45元,乙种图书每套40元.这些钱最多能买甲种图书多少套
问题1: 设可购买甲种图书x套,则购买甲种图书用的钱为______元,购买乙种图书________套,购买乙种图书用的钱为________ 元.
45x
(12-x)
40(12-x)
知识讲解
问题2: 购买甲、乙两种图书所用钱数与500元有什么关系
甲图书所用钱数 + 乙图书所用钱数 ≤ 500.
问题3: 你能用不等式把这种关系表示出来吗
45x+40(12-x)≤ 500
问题4:解上面列出的不等式,并根据解集确定实际问题的答案.
解得x≤ 4,故最多购买甲图书4套.
通过以上分析,你可以总结一下应用一元一次不等式解决实际问题的步骤吗?
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
例1 某商场决定采购一批电冰箱,优惠销售给农民朋友. 商场从厂家直接购进甲、乙、丙三种不同型号的电冰箱共80台,其中,甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132000元,已知甲、乙、丙三种电冰箱每台的出厂价格分别为1200元,1600元,2000元. 那么该商场购进的乙种电冰箱至少为多少台?
解析:题中的等量关系,
甲冰箱数 + 乙冰箱数 + 丙冰箱数 = 80
甲冰箱数 = 2×乙冰箱数
题中的不等关系,
1200×甲冰箱数+1600×乙冰箱数+
2000×丙冰箱数≤132000
根据题意列不等式,得
1200×2x+1600x+2000(80-3x)≤132000.
解这个不等式,得
x≥14.
答:至少购进乙种电冰箱14台.
解:设购买乙种电冰箱x台,则购买甲种电冰箱是2x台,丙种电冰箱是(80-3x)台.
随 堂 训 练
1.某市天然气公司在居民小区安装天然气管道时采用一种鼓励居民使用天然气的收费方法若整个小区每户都安装收整体初装费10 000元再对每户收费500元.某小区按这种收费方法全部安装天然气后每户平均支付不足1 000元则这个小区的住户数( )
A.至少20户 B.至多20户
C.至少21户 D.至多21户
C
解析:设这个小区的住户数为x户则1 000x10 000.
随堂训练
2.某商品的标价比成本价高m%根据市场需要该商品需降价n%出售为了不亏本n应满足( )
A.n≤m B.n≤ C.n≤ D.n≤
B
解析:设该商品的成本价为a元由题意可得
3.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,根据题意,得
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
随堂训练
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
小琴最多打了5min的电话.
4.某汽车租赁公司要购买轿车和面包车共10辆,其中轿
车至少要购买3辆,轿车每辆7万元,面包车每辆4万
元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由。
(2)如果每辆轿车的日租金为200元,每辆面包车的日租
金为110元,假设新购买的这10辆车每日都可租出,
要使这10辆车的日租金收入不低于1500元,那么应
选择以上哪种购买方案?
解: (1)设轿车要购买x辆,那么面包车要购买(10-x)辆,
7x+4(10-x)≤55,解得 x≤5,
又x≥3,则x=3,4,5,
∴有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2)方案一的日租金为3×200+7×110=1370;
方案二的日租金为:4×200+6×110=1460;
方案三的日租金为:5×200+5×110=1550;
为保证日租金不低于1500,应选方案三.
课 堂 小 结
列一元一次不等式解应用题的一般步骤:
(1)审题,找不等关系;
(2)设未知数,用未知数表示有关代数式
(3)列不等式
(4)解不等式
(5)根据实际情况写出答案
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
