20.2数据的集中趋势与离散程度(第4课时平均数、中位数、众数的应用) 教学课件 沪科版初中数学八年级(下)
文档属性
| 名称 | 20.2数据的集中趋势与离散程度(第4课时平均数、中位数、众数的应用) 教学课件 沪科版初中数学八年级(下) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 19:36:48 | ||
图片预览







文档简介
(共21张PPT)
第20章 数据的初步分析
第4课时 平均数、中位数、众数的应用
20.2 数据的集中趋势与离散程度
学 习 目 标
1
2
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.(难点)
会用样本估计总体.(重点、难点)
3.众数:一组数据中出现次数最多的数据称为这组数据的众数.
2.中位数:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
1.加权平均数:一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则 叫做这n个数的加权平均数.
知识回顾
问题:有6 户家庭的年收入分别为(单位:万元):4,
5,5,6,7,50.你认为这6户家庭的年收入水 平大概是多少?
(3)用众数估计: 众数= 5(万元).
(1)用平均数估计: (万元);
(2)用中位数估计:中位数= (万元);
导入新课
知识讲解
用样本估计总体
111
1
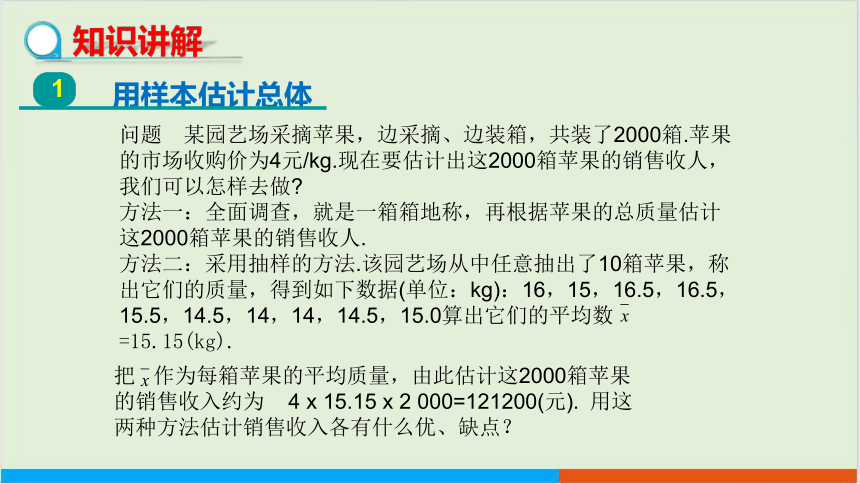
问题 某园艺场采摘苹果,边采摘、边装箱,共装了2000箱.苹果的市场收购价为4元/kg.现在要估计出这2000箱苹果的销售收人,我们可以怎样去做
方法一:全面调查,就是一箱箱地称,再根据苹果的总质量估计这2000箱苹果的销售收人.
方法二:采用抽样的方法.该园艺场从中任意抽出了10箱苹果,称出它们的质量,得到如下数据(单位:kg):16,15,16.5,16.5,15.5,14.5,14,14,14.5,15.0算出它们的平均数 =15.15(kg).
把 作为每箱苹果的平均质量,由此估计这2000箱苹果的销售收入约为 4 x 15.15 x 2 000=121200(元). 用这两种方法估计销售收入各有什么优、缺点?
问题1:八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
他们都认为自己的数学成绩比其他两位同学好,
他们的依据是什么?
平均数、中位数和众数的选择
11
2
分析:小华成绩的众数是_____,中位数是_____,平均数是_____;
小明成绩的众数是_____,中位数是_____,平均数是_____;
小丽成绩的众数是_____,中位数是_____,平均数是_____.
98
62
95
98
89.4
84.2
99
85
77
解:因为他们之中,小华的平均数最大,小明的中位数最大,小丽的众数最大,所以都认为自己的成绩比其他两位同学好.
你认为谁的数学成绩最好呢?
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
例1
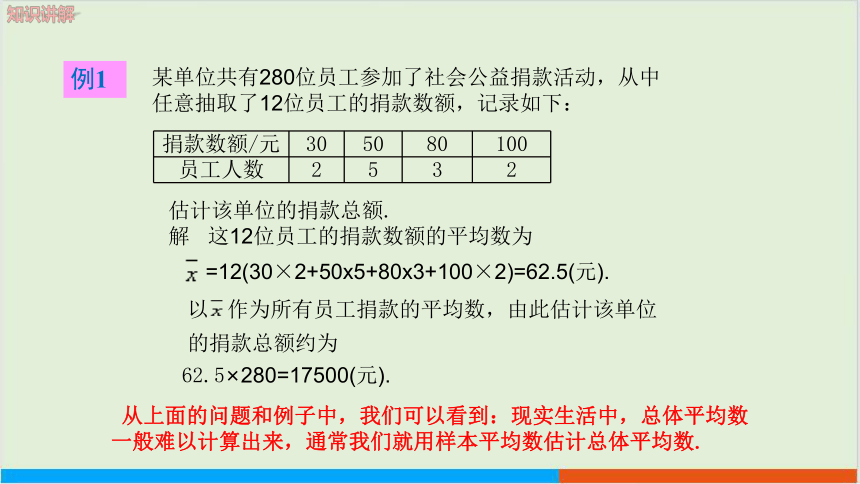
某单位共有280位员工参加了社会公益捐款活动,从中
任意抽取了12位员工的捐款数额,记录如下:
捐款数额/元 30 50 80 100
员工人数 2 5 3 2
估计该单位的捐款总额.
解 这12位员工的捐款数额的平均数为
=12(30×2+50x5+80x3+100×2)=62.5(元).
62.5×280=17500(元).
以
作为所有员工捐款的平均数,由此估计该单位
的捐款总额约为
从上面的问题和例子中,我们可以看到:现实生活中,总体平均数一般难以计算出来,通常我们就用样本平均数估计总体平均数.
公园有甲、乙两队游客在做团体游戏,两队游客的年龄(单位:岁)如下:
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
例2
(1)分别算出两队游客年龄的平均数、众数和中位数.
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
分析:(1)将两组数据分别代入平均数的计算公式计算;根据中位数和众数的定义来分别确定甲、乙两队的中位数和众数.
(2)要判断平均数能否代表各组年龄的特征,就是要看平均数是否与各组数据反映的实际意义相吻合.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征.
对于乙队游客而言,10 人中有8 人的年龄在9 岁以下,而说他们的平均年龄是15 岁,会让人误认为这队游客的年龄都在15 岁左右,所以乙队的平均数不能代表该队游客年龄的特征. 可选用中位数或众数来代表乙队游客的年龄特征.
解:(1)甲队游客年龄的平均数为
乙队游客年龄的平均数为
,众数为8岁,中位数为7.5岁.
,众数为15岁,中位数为15岁;
某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
例3
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
分析:本题通过分析样本数据的平均数、中位数、众数来估计______的情况.
确定一个适当的月销售目标是一个关键问题,如果目标定得太高,多数营业员完不成任务,会使营业员失去信心;如果目标定得太低,不能发挥营业员的潜力.
总体
0
4
2
6
人数
销售额/万元
解:整理上面的数据得以下图表(请补充完整):
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
13
14
15
16
17
18
19
22
23
24
26
28
30
32
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:样本数据的众数是_____,中位数是_____,利用计算器求得这组数据的平均数约是_____.
可以推测,这个服装部营业员的月销售额为_____万元的人数最多,中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
18
20
大
三分之一
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:这个目标可以定为每月____万元(中位数).可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
20
20
二分之一
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
3.一销售某品牌冰箱的公司有营销人员10人,销售部为制定营销人员月销售冰箱定额(单位:台),统计了10人某月的销售量如表:
每人销售台数 4 5 8 12 16 19
人数 1 1 4 2 1 1
(1)求这10名营销人员该月销售冰箱的平均数、众数和中位数;
(2)如果想让一半以上的营销人员都能达到月销售目标,你认为(1)中的平均数、中位数哪个最适合作为月销售目标?请说明理由.
解:(1)这10名营业员该月销售量数据的平均数=
∵8台出现了4次,出现的次数最多,∴众数是8台;10个数据按从小到大的顺序排列后,第5、第6个数都是8,所以中位数是8台;
(2)如果想让一半左右的营业员都能达到销售目标,平均数、中位数、众数中,中位数最适合作为月销售目标;理由如下:
因为中位数为8台,月销售量大于和等于8台的人数超过一半,
所以中位数最适合作为月销售目标,有一半以上的营业员能达到销售目标.
1.根据实际情况填写(填平均数、中位数、众数).
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注 .
③被招聘的员工关注公司员工工资的 .
中位数
平均数
众数
2.我校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.中位数 C.方差 D.平均数
B
随堂训练
3.老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 平均每条鱼的质量
第一次捕捞 10 1.7千克
第二次捕捞 25 1.8千克
第三次捕捞 15 2.0千克
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克;
(2)鱼塘里这种鱼的总产量多少千克?
解:(1)鱼的平均重量为:
(2)鱼的总重量为2000×95%×1.84=3496千克.
答:鱼塘里这种鱼的总质量估计是3496千克.
答:鱼塘里这种鱼平均每条的质量约1.84千克;
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
课堂小结
用样本估计总体
第20章 数据的初步分析
第4课时 平均数、中位数、众数的应用
20.2 数据的集中趋势与离散程度
学 习 目 标
1
2
了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.(难点)
会用样本估计总体.(重点、难点)
3.众数:一组数据中出现次数最多的数据称为这组数据的众数.
2.中位数:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
1.加权平均数:一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则 叫做这n个数的加权平均数.
知识回顾
问题:有6 户家庭的年收入分别为(单位:万元):4,
5,5,6,7,50.你认为这6户家庭的年收入水 平大概是多少?
(3)用众数估计: 众数= 5(万元).
(1)用平均数估计: (万元);
(2)用中位数估计:中位数= (万元);
导入新课
知识讲解
用样本估计总体
111
1
问题 某园艺场采摘苹果,边采摘、边装箱,共装了2000箱.苹果的市场收购价为4元/kg.现在要估计出这2000箱苹果的销售收人,我们可以怎样去做
方法一:全面调查,就是一箱箱地称,再根据苹果的总质量估计这2000箱苹果的销售收人.
方法二:采用抽样的方法.该园艺场从中任意抽出了10箱苹果,称出它们的质量,得到如下数据(单位:kg):16,15,16.5,16.5,15.5,14.5,14,14,14.5,15.0算出它们的平均数 =15.15(kg).
把 作为每箱苹果的平均质量,由此估计这2000箱苹果的销售收入约为 4 x 15.15 x 2 000=121200(元). 用这两种方法估计销售收入各有什么优、缺点?
问题1:八年级某班的教室里,三位同学正在为谁的数学成绩好而争论,他们的五次数学成绩分别是:
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
他们都认为自己的数学成绩比其他两位同学好,
他们的依据是什么?
平均数、中位数和众数的选择
11
2
分析:小华成绩的众数是_____,中位数是_____,平均数是_____;
小明成绩的众数是_____,中位数是_____,平均数是_____;
小丽成绩的众数是_____,中位数是_____,平均数是_____.
98
62
95
98
89.4
84.2
99
85
77
解:因为他们之中,小华的平均数最大,小明的中位数最大,小丽的众数最大,所以都认为自己的成绩比其他两位同学好.
你认为谁的数学成绩最好呢?
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
例1
某单位共有280位员工参加了社会公益捐款活动,从中
任意抽取了12位员工的捐款数额,记录如下:
捐款数额/元 30 50 80 100
员工人数 2 5 3 2
估计该单位的捐款总额.
解 这12位员工的捐款数额的平均数为
=12(30×2+50x5+80x3+100×2)=62.5(元).
62.5×280=17500(元).
以
作为所有员工捐款的平均数,由此估计该单位
的捐款总额约为
从上面的问题和例子中,我们可以看到:现实生活中,总体平均数一般难以计算出来,通常我们就用样本平均数估计总体平均数.
公园有甲、乙两队游客在做团体游戏,两队游客的年龄(单位:岁)如下:
甲队:13,13,14,15,15,15,15,16,17,17;
乙队:5,6,6,7,7,8,8,8,46,49.
例2
(1)分别算出两队游客年龄的平均数、众数和中位数.
(2)甲、乙两队游客年龄的平均数能代表他们各自的年龄特征吗?如果不能,哪个数据能代表?
分析:(1)将两组数据分别代入平均数的计算公式计算;根据中位数和众数的定义来分别确定甲、乙两队的中位数和众数.
(2)要判断平均数能否代表各组年龄的特征,就是要看平均数是否与各组数据反映的实际意义相吻合.
(2)甲队游客年龄的平均数能代表他们的年龄特征,乙队游客年龄的平均数不能代表他们的年龄特征.
对于乙队游客而言,10 人中有8 人的年龄在9 岁以下,而说他们的平均年龄是15 岁,会让人误认为这队游客的年龄都在15 岁左右,所以乙队的平均数不能代表该队游客年龄的特征. 可选用中位数或众数来代表乙队游客的年龄特征.
解:(1)甲队游客年龄的平均数为
乙队游客年龄的平均数为
,众数为8岁,中位数为7.5岁.
,众数为15岁,中位数为15岁;
某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
例3
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
分析:本题通过分析样本数据的平均数、中位数、众数来估计______的情况.
确定一个适当的月销售目标是一个关键问题,如果目标定得太高,多数营业员完不成任务,会使营业员失去信心;如果目标定得太低,不能发挥营业员的潜力.
总体
0
4
2
6
人数
销售额/万元
解:整理上面的数据得以下图表(请补充完整):
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
13
14
15
16
17
18
19
22
23
24
26
28
30
32
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:样本数据的众数是_____,中位数是_____,利用计算器求得这组数据的平均数约是_____.
可以推测,这个服装部营业员的月销售额为_____万元的人数最多,中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
18
20
大
三分之一
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:这个目标可以定为每月____万元(中位数).可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
20
20
二分之一
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
销售额 /万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
3.一销售某品牌冰箱的公司有营销人员10人,销售部为制定营销人员月销售冰箱定额(单位:台),统计了10人某月的销售量如表:
每人销售台数 4 5 8 12 16 19
人数 1 1 4 2 1 1
(1)求这10名营销人员该月销售冰箱的平均数、众数和中位数;
(2)如果想让一半以上的营销人员都能达到月销售目标,你认为(1)中的平均数、中位数哪个最适合作为月销售目标?请说明理由.
解:(1)这10名营业员该月销售量数据的平均数=
∵8台出现了4次,出现的次数最多,∴众数是8台;10个数据按从小到大的顺序排列后,第5、第6个数都是8,所以中位数是8台;
(2)如果想让一半左右的营业员都能达到销售目标,平均数、中位数、众数中,中位数最适合作为月销售目标;理由如下:
因为中位数为8台,月销售量大于和等于8台的人数超过一半,
所以中位数最适合作为月销售目标,有一半以上的营业员能达到销售目标.
1.根据实际情况填写(填平均数、中位数、众数).
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注 .
③被招聘的员工关注公司员工工资的 .
中位数
平均数
众数
2.我校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.中位数 C.方差 D.平均数
B
随堂训练
3.老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 平均每条鱼的质量
第一次捕捞 10 1.7千克
第二次捕捞 25 1.8千克
第三次捕捞 15 2.0千克
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克;
(2)鱼塘里这种鱼的总产量多少千克?
解:(1)鱼的平均重量为:
(2)鱼的总重量为2000×95%×1.84=3496千克.
答:鱼塘里这种鱼的总质量估计是3496千克.
答:鱼塘里这种鱼平均每条的质量约1.84千克;
平均数、中位数和众数的应用
平均数、中位数、众数的实际应用
平均数、中位数、众数的特征
课堂小结
用样本估计总体
